文档内容
五年(2019-2023)年高考真题分项汇编
专题 15 概率与统计(文解答题)
概率与统计题型主要包含随机抽样,相关性分析,独立性检验等统计与概率等主要考查题型为:
考点01 统计案例及应用
考点02 相关关系与回归分析
考点03 独立性检验
考点 01:统计案例及应用
1 (2021年全国高考乙卷文科)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有
无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
. .
旧设
9.8 103 10.0 102 9.9 9.8 10.0 10.1 10.2 9.7
备
.
新设
10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 104 10.5
备
旧设备和新设备生产产品 的该项指标的样本平均数分别记为 和 ,样本方差分别记为 和 .
(1)求 , , , ;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果 ,则认
为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
【答案】(1) ;(2)新设备生产产品的该项指标的均值较旧设备
有显著提高.
【解析】:(1) ,
,,
.
(2)依题意, , ,
,所以新设备生产产品的该项指标的均值较旧设备有显著提高.
2 (2020年高考数学课标Ⅰ卷文科)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,
B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,
50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业
务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工
业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承
接加工业务?
【答案】(1)甲分厂加工出来的 级品的概率为 ,乙分厂加工出来的 级品的概率为 ;(2)
选甲分厂,理由见解析.
【解析】(1)由表可知,甲厂加工出来的一件产品为 级品的概率为 ,乙厂加工出来的一件
产品为 级品的概率为 ;
(2)甲分厂加工 件产品 的总利润为
元,
所以甲分厂加工 件产品的平均利润为 元每件;乙分厂加工 件产品的总利润为
元,
所以乙分厂加工 件产品的平均利润为 元每件.
故厂家选择甲分厂承接加工任务.
3 (2019年高考数学课标Ⅲ卷文科)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下实验:将
200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶
液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小
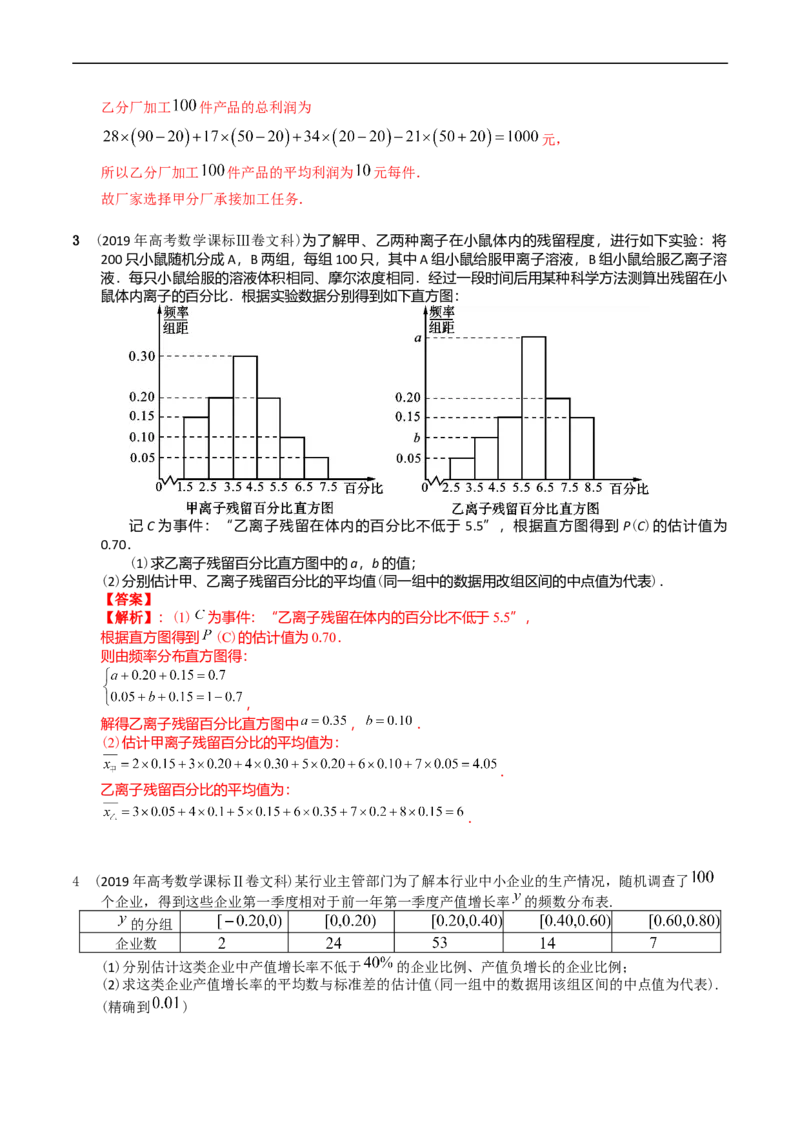
鼠体内离子的百分比.根据实验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于 5.5”,根据直方图得到 P(C)的估计值为
0.70.
(1)求乙离子残留百分比直方图中的a,b的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用改组区间的中点值为代表).
【答案】
【解析】:(1) 为事件:“乙离子残留在体内的百分比不低于5.5”,
根据直方图得到 (C)的估计值为0.70.
则由频率分布直方图得:
,
解得乙离子残留百分比直方图中 , .
(2)估计甲离子残留百分比的平均值为:
.
乙离子残留百分比的平均值为:
.
4 (2019年高考数学课标Ⅱ卷文科)某行业主管部门为了解本行业中小企业的生产情况,随机调查了
个企业,得到这些企业第一季度相对于前一年第一季度产值增长率 的频数分布表.
的分组
企业数
(1)分别估计这类企业中产值增长率不低于 的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).
(精确到 )附: .
【答案】
【解析】:(1)根据产值增长率频数分布表得,所调查的 个企业中产值增长率不低于 的企业
频率为 .产值负增长的企业频率为 .
用样本频率分布估计总体分布得这类企业中产值增长率不低于 的企业比例为 ,产值负增长
的企业比例为 .
(2) ,
,
,
所以,这类企业产值增长率的平均数与标准差的估计值分别为 , .
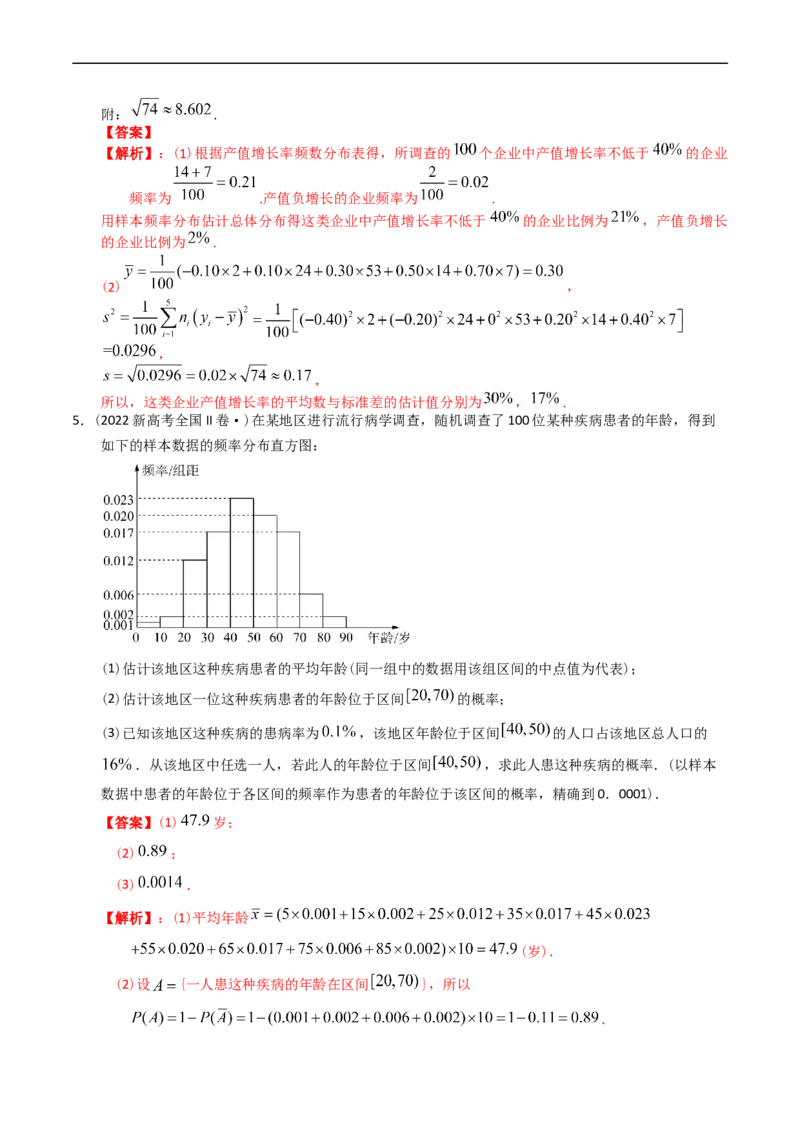
5.(2022新高考全国II卷·)在某地区进行流行病学调查,随机调查了100位某种疾病患者的年龄,得到
如下的样本数据的频率分布直方图:
(1)估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)估计该地区一位这种疾病患者的年龄位于区间 的概率;
(3)已知该地区这种疾病的患病率为 ,该地区年龄位于区间 的人口占该地区总人口的
.从该地区中任选一人,若此人的年龄位于区间 ,求此人患这种疾病的概率.(以样本
数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).
【答案】(1) 岁;
(2) ;
(3) .
【解析】:(1)平均年龄
(岁).
(2)设 {一人患这种疾病的年龄在区间 },所以
.(3)设 任选一人年龄位于区间 , 任选一人患这种疾病 ,
则由条件概率公式可得
.
考点 02 相关关系与回归分析
1.(2022年高考全国乙卷(文)·)某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区
某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位: )和材积量
(单位: ),得到如下数据:
样
本 总
1 2 3 4 5 6 7 8 9 10
号 和
i
根
部
横 0. 0. 0. 0. 0. 0. 0. 0.
. .
截 0 0 0 0 0 005 005 0 0 0 0.6
面
4 6 4 8 8 7 7 6
积
材
0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
积
2 4 2 5 5 3 3 4 4 4 3.9
量
5 0 2 4 1 4 6 6 2 0
并计算得 .
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为
.已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材
积量的估计值.附:相关系数 .
【答案】(1) ;
(2)
(3)
【解析】:【小问1详解】
样本中10棵这种树木的根部横截面积的平均值
样本中10棵这种树木的材积量的平均值
据此可估计该林区这种树木平均一棵的根部横截面积为 ,
平均一棵的材积量为
【小问2详解】
则
【小问3详解】
设该林区这种树木的总材积量的估计值为 ,
又已知树木的材积量与其根部横截面积近似成正比,
可得 ,解之得 .
则该林区这种树木 的总材积量估计为
2.(2020年高考数学课标Ⅱ卷文科·)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所
增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随
机抽样的方法抽取20个作为样区,调查得到样本数据(x,y)(i=1,2,…,20),其中x和y分别表示
i i i i
第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得 ,, , , .
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平
均数乘以地块数);
(2)求样本(x,y)(i=1,2,…,20)的相关系数(精确到0.01);
i i
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野
生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r= , ≈1.414.
【答案】(1) ;(2) ;(3)详见解析
【解析】(1)样区野生动物平均数为 ,
地块数为200,该地区这种野生动物的估计值为
(2)样本 (i=1,2,…,20)的相关系数为
(3)由(2)知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性,
由于各地块间植物覆盖面积差异很大,从俄各地块间这种野生动物的数量差异很大,
采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,
从而可以获得该地区这种野生动物数量更准确的估计.
【点晴】本题主要考查平均数的估计值、相关系数的计算以及抽样方法的选取,考查学生数学运算能
力,是一道容易题.
考点 03 独立性检验
1.(2022年全国高考甲卷(文)·)甲、乙两城之间的长途客车均由A和B两家公司运营,为了解这两家公
司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到下面列联表:
准点班次数 未准点班次数
A 240 20
B 210 30
(1)根据上表,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;(2)能否有 的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?
附: ,
0.100 0.050 0.010
2.706 3.841 6.635
【答案】
(1)A,B两家公司长途客车准点的概率分别为 , (2)有
【解析】根据表中数据,A共有班次260次,准点班次有240次,
设A家公司长途客车准点事件为M,则 ;
B共有班次240次,准点班次有210次,
设B家公司长途客车准点事件为N,
则 .
A家公司长途客车准点的概率为 ;
B家公司长途客车准点的概率为 .
(2)列联表
未准点班
准点班次数 合计
次数
A 240 20 260
B 210 30 240
合计 450 50 500
= ,
根据临界值表可知,有 的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.
2.(2020年新高考I卷(山东卷)·)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行
调研,随机抽查了 天空气中的 和 浓度(单位: ),得下表:32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中 浓度不超过 ,且 浓度不超过 ”的概率;
(2)根据所给数据,完成下面的 列联表:
(3)根据(2)中 的列联表,判断是否有 的把握认为该市一天空气中 浓度与 浓度有关?
附: ,
0.050 0.010 0.
001
3.841 6.635
10.828
【答案】(1) ;(2)答案见解析;(3)有.
【解析】:(1)由表格可知,该市100天中,空气中的 浓度不超过75,且 浓度不超过150
的天数有 天,
所以该市一天中,空气中的 浓度不超过75,且 浓度不超过150的概率为 ;
(2)由所给数据,可得 列联表为:
合计
64 16 8010 10 20
合计 74 26 100
(3)根据 列联表中的数据可得
,
因为根据临界值表可知,有 的把握认为该市一天空气中 浓度与 浓度有关.
3 .(2020新高考II卷(海南卷)·)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调
研,随机抽查了 天空气中的 和 浓度(单位: ),得下表:
(1)估计事件“该市一天空气中 浓度不超过 ,且 浓度不超过 ”的概率;
(2)根据所给数据,完成下面的 列联表:
(3)根据(2)中的列联表,判断是否有 的把握认为该市一天空气中 浓度与 浓度有关?附: ,
【答案】(1) ;(2)答案见解析;(3)有.
【解析】:(1)由表格可知,该市100天中,空气中的 浓度不超过75,且 浓度不超过150
的天数有 天,
所以该市一天中,空气中的 浓度不超过75,且 浓度不超过150的概率为 ;
(2)由所给数据,可得 列联表为:
合计
64 16 80
10 10 20
合计 74 26 100
(3)根据 列联表中的数据可得
,
因为根据临界值表可知,有 的把握认为该市一天空气中 浓度与 浓度有关.
【题目栏目】统计\相关关系、回归分析与独立性检验\独立性检验
4.(2021年高考全国甲卷文科·)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了
比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
一级品 二级品 合计
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99% 的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附:
0.050 0.010 0.001
k 3.841 6.635 10.828
【答案】(1)75%;60%;
(2)能.
解析:(1)甲机床生产的产品中的一级品的频率为 ,
乙机床生产的产品中的一级品的频率为 .
(2) ,
故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异.
5.(2020年高考数学课标Ⅲ卷文科·)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当
天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次
[0,200] (200,400] (400,600]
空气质量等级
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称
这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把
握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?人次≤400 人次>400
空气质量好
空气质量不好
附: ,
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
【答案】(1)该市一天的空气质量等级分别为 、 、 、 的概率分别为 、 、 、 ;
(2) ;(3)有,理由见解析.
【解析】(1)由频数分布表可知,该市一天的空气质量等级为 的概率为 ,等级为
的概率为 ,等级为 的概率为 ,等级为 的概率为
;
(2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为
(3) 列联表如下:
人次 人次
空气质量不好
空气质量好
,
因此,有 的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
6.(2019年高考数学课标Ⅰ卷文科·)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,
每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 不满意
男顾客 40 10女顾客 30 20
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有 的把握认为男、女顾客对该商场服务的评价有差异?
附: .
0.050 0.010 0.001
3.841 6.635 10.828
【答案】
【解析】(1)由调查数据,男顾客中对该商场服务满意的比率为 ,因此男顾客对该商场服务
满意的概率的估计值为0.8.女顾客中对该商场服务满意的比率为 ,因此女顾客对该商场服
务满意的概率的估计值为0.6.
(2) .
由于 ,故有95%的把握认为男、女顾客对该商场服务的评价有差异.