文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考II 卷专用)
黄金卷03
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.已知,则( ).
A. B. C.2 D.1
【答案】C
【分析】先根据复数的乘法运算求出复数,再根据共轭复数的定义和复数的模的公司及即可得解.
【详解】由,得,
则,所以.
故选:C.
2.集合,集合,则集合中元素的个数为( )
A.2 B.3 C.4 D.5
【答案】B
【分析】根据给定条件,利用交集的意义求出即得.
【详解】集合,,则,
所以集合中元素的个数为3.
故选:B
3.已知等差数列的前n项和为,对任意的,均有成立,则的值的取值范围是( )
A. B.
C. D.
【答案】B
【分析】根据已知得出,公差,然后返和(即)分类计算.
【详解】由题意知是等差数列的前n项和中的最小值,必有,公差,
若,此时,,是等差数列的前n项和中的最小值,
此时,即,则;
若,,此时是等差数列的前n项和中的最小值,
此时,,即,
则,综上可得:的取值范围是,
故选:B.
4.为进一步在全市掀起全民健身热潮,兴义市于9月10日在万峰林举办半程马拉松比赛.已知本次比赛设
有4个服务点,现将6名志愿者分配到4个服务点,要求每位志愿者都要到一个服务点服务,每个服务点
都要安排志愿者,且最后一个服务点至少安排2名志愿者,有( )种分配方式
A.540 B.660 C.980 D.1200
【答案】B
【分析】按照最后一个服务区有2名志愿者和3名志愿者进行分配,即和,分别求出其方法种数,即可得
出答案.
【详解】由题知可按照最后一个服务区有2名志愿者和3名志愿者进行分配,
①,有;
②,有,
共有(种).
故选:B.
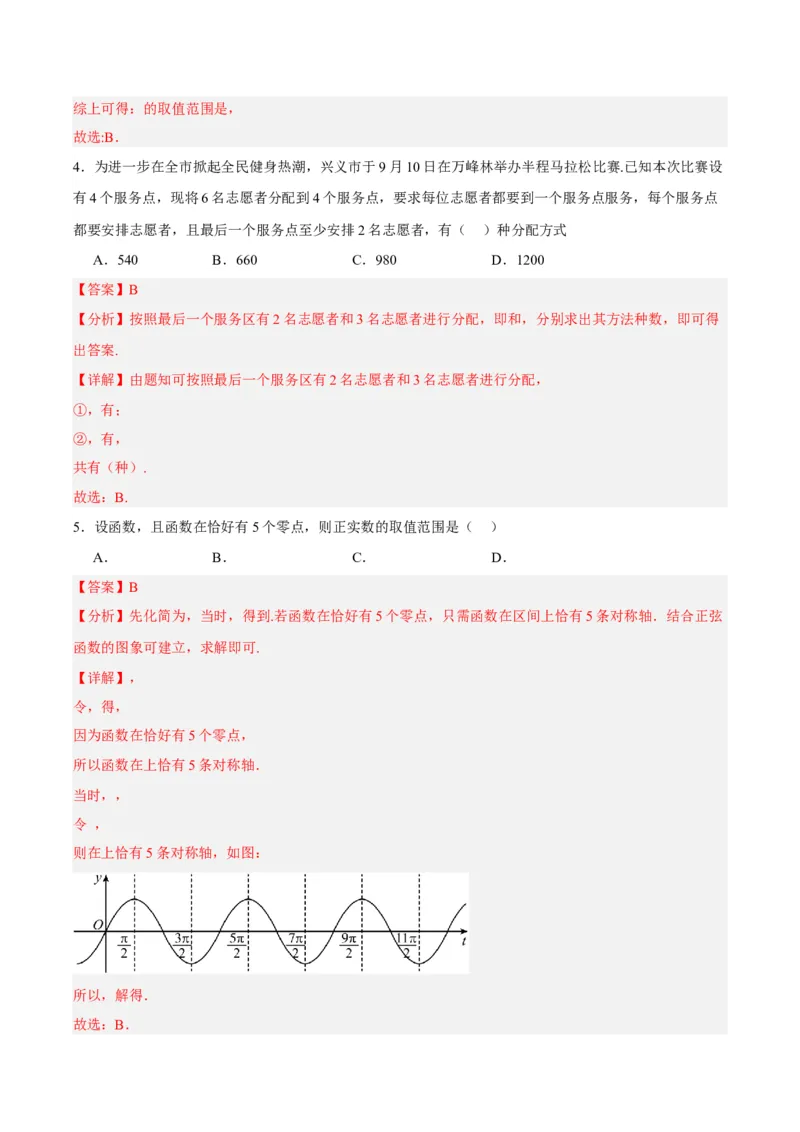
5.设函数,且函数在恰好有5个零点,则正实数的取值范围是( )
A. B. C. D.
【答案】B
【分析】先化简为,当时,得到.若函数在恰好有5个零点,只需函数在区间上恰有5条对称轴.结合正弦
函数的图象可建立,求解即可.
【详解】,
令,得,
因为函数在恰好有5个零点,
所以函数在上恰有5条对称轴.
当时,,
令 ,
则在上恰有5条对称轴,如图:
所以,解得.
故选:B.6.如图所示,是双曲线的左、右焦点,的右支上存在一点满足与双曲线左支的交点满足,则双曲线的离
心率为( )
A. B.2 C. D.
【答案】D
【分析】利用正弦定理及已知可得,令,由双曲线定义及,应用勾股定理列方程求得,进而求离心率.
【详解】中,中,
所以,,
又,则,又,
所以,令,则,,
而,由,则,,
可得,即 .
故选:D
7.已知函数,设,则,,的大小关系为( )
A. B. C. D.
【答案】A
【分析】首先判断函数的奇偶性和单调性,再判断自变量的大小,即可根据函数的单调性,比较大小.
【详解】依题意,得的定义域为,函数为偶函数,且在上为增函数,
而,
因为,所以,即,
因为在上为增函数,且,所以,
,
因为,所以,所以,
所以,所以,
故选:A.
8.设函数,直线是曲线的切线,则的最小值为( )
A. B.C. D.
【答案】C
【分析】先设切点写出切线方程,再求的解析式,最后通过求导判断单调性求出最小值.
【详解】令的切点为,因为,
所以过切点的切线方程为,
即,所以,
所以,
令,则,
所以当时恒成立,此时单调递减,
当时恒成立,此时单调递增,
所以,所以,
故选:C
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.在的展开式中,各项系数的和为1,则( )
A. B.展开式中的常数项为
C.展开式中的系数为160 D.展开式中无理项的系数之和为
【答案】BC
【分析】先根据各项系数和结赋值法得判断A,然后结合二项式展开式的通项公式求解常数项、含的系数
及无理项系数之和判断BCD.
【详解】根据题意令,得的展开式中各项系数和为,则,A错误;
则,
又的展开式的通项为,,
所以展开式中的常数项为,B正确;
含的项为,其系数为160,C正确;
展开式中无理项的系数之和为,D错误.
故选:BC.
10.如图,正三棱柱的底面边长为1,高为3,为棱的中点,分别在棱上,且满足取得最小值.记四棱锥、
三棱锥的体积分别为,则( )A. B. C. D.
【答案】ABD
【分析】根据三棱柱的体积公式即可判断A,根据平面展开图可得线段最短时,即可根据锥体体积公式判断
BCD.
【详解】正三棱柱的体积为,由图可知,所以,所以A正确;
沿着侧棱将棱柱展开得到一个矩形,连接,
因为取得最小值,即线段,
由于四边形为边长为3的正方形,所以,因为为的中点,所以
,,
,所以B正确,C不正确,D正确.
故选:ABD.
11.已知抛物线的准线为,焦点为F,过点F的直线与抛物线交于,两点,于,则下列说法正确的是(
)
A.若,则
B.以PQ为直径的圆与准线l相切
C.设,则
D.过点与抛物线C有且仅有一个公共点的直线至多有2条【答案】ABC
【分析】根据过焦点的直线与抛物线的相交的交点坐标关系、圆的几何性质逐项判断即可.
【详解】由题意,抛物线的准线为,所以,抛物线C的方程为,焦点为,
过作于,
则由抛物线的定义可得,故A正确;
,则以PQ为直径的圆的半径,
线段PQ的中点坐标为,
则线段PQ的中点到准线的距离为,
所以以PQ为直径的圆与准线l相切,故B正确;
抛物线的焦点为,,
当且仅当M,P,F三点共线时取等号,所以,故C正确;
对于D,当直线斜率不存在时,直线方程为,与抛物线只有一个交点,
当直线斜率存在时,设直线方程为,
联立消去x,并整理得,
当时,方程的解为,此时直线与抛物线只有一个交点,
当时,则,解得,
综上所述,过点与抛物线C有且仅有一个公共点的直线有3条,故D错误.
故选:ABC.
12.泰勒公式通俗的讲就是用一个多项式函数去逼近一个给定的函数,也叫泰勒展开式,下面给出两个泰
勒展开式
由此可以判断下列各式正确的是( ).
A.(i是虚数单位) B.(i是虚数单位)C. D.
【答案】ACD
【分析】对于A、B,将关于的泰勒展开式两边求导得的泰勒展开式,再验证结论是否正确;
对于C,由 ,再代入关于的泰勒展开式验证是否成立;
对于D,由,证明
即可.
【详解】对于A、B,由,
两边求导得,
,
,
又,
,
,故A正确,B错误;
对于C,已知,则.
因为 ,则,即成立,故C正确;
故C正确;
对于D,,,
,
当,;;;
,,
所以,所以成立,故D正确.
故选:ACD.
【点睛】利用泰勒公式证明不等式方法点睛:
应用泰勒公式时要选好,有时可能需要结合题目给出信息进行相关变形,再代入验证,利用展开项的特征
进行适当的放缩,证明不等式成立.
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.设向量在向量上的投影向量为,则 .
【答案】1
【分析】利用向量在向量上的投影向量计算公式建立方程,解出即可.
【详解】向量在向量上的投影向量为,则,解得.
故答案为:
14.四个面都为直角三角形的四面体称之为鳌臑.在鳌臑中,平面,,,鳌臑的四个顶点都在同一个球面
上,则该球的表面积是 .
【答案】
【分析】根据题意,把鳌臑补成一个长方体,则长方体的外接球即是鳌臑的外接球,从而求出鳌臑的外接
球半径为,再利用球的体积公式即可求出结果.
【详解】把鳌臑补成一个长方体,如图所示:
则长方体的外接球即是鳌臑的外接球,
又,,
长方体的外接球半径,
鳌臑的外接球半径为,
则该球的表面积是,
故答案为:.
15.已知圆,过点的直线交圆于两点,且,请写出一条满足上述条件的直线的方程 .
【答案】(答案不唯一,也满足)
【分析】分别讨论直线l斜率存在、不存在的情况,设C到直线的距离为d,由得,结合点线距离公式即
可求解判断.【详解】由题意得,半径,,
故在圆外,设O到直线的距离为d,
由得,即,
解得,
当直线l斜率不存在时,即,此时,符合题意;
当直线l斜率存在时,设为,即,
则, 即,解得,故直线为.
故答案为:(答案不唯一,也满足)
16.已知函数及其导函数的定义域均为,记,若为偶函数,,且,则 .
【答案】6
【分析】根据为偶函数,可得,两边求导后可得,令,得,令,得;由,可得的周期为6,进而得,从而
可得答案.
【详解】因为为偶函数,所以,
两边同时求导得,即,
所以,即,
令,得,
令,得,又因为,所以,
由,所以,
所以的周期为6,则,
而,所以,
所以.
故答案为:6.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.在(1);(2);(3)这三个条件中任选一个,补充在下面的问题中,并解答问题.在中,内角的对
边分别为,且满足
(1)求角;
(2)若的外接圆周长为,求边上的中线长.
【答案】(1)所选条件见解析,;
(2).
【分析】(1)根据所选条件,应用正弦边角关系、三角形面积公式、向量数量积定义、三角恒等变换化
简条件求角;(2)由已知易得为顶角为的等腰三角形,是中点,则,利用向量数量积的运算律求中线长度.
【详解】(1)选(1),则,
所以,而,则,
所以 ;
选(2),则,
所以,而,则;
选(3),则,,
所以,
所以,则,
而,则.
(2)由,则,故,,即,
结合(1)易知:为顶角为的等腰三角形,如下图,是中点,
的外接圆周长为,若外接圆半径为,则,
所以,而,
所以,
则 ,即求边上的中线长为.
18.若数列的前项和满足.
(1)证明:数列是等比数列;
(2)设,记数列的前项和为,证明:对任意的正整数,都有.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)根据递推式关系再写一项做差,之后利用等比数列定义证明;
(2)先求出的表达式,之后进行裂项求和即可.
【详解】(1)证明:由,当时,可得;
当时,,所以,
∴时,,
∴数列是以为首项,为公比的等比数列;
∴,∴.(2)证明:由(1)知,,∴,
∴,
∴,
因为,所以,所以即成立.
所以对任意的正整数,都有得证.
19.2023年9月8日,第19届亚运会火炬传递启动仪式在杭州西湖景区涌金公园广场成功举行.火炬传递
首日传递从杭州西湖涌金公园广场出发,沿南山路—湖滨路—环城西路—北山街—西泠桥—孤山路传递,
在“西湖十景”之一的平湖秋月收火.杭州亚运会火炬首日传递共有106棒火炬手参与.
(1)组委会从全省火炬手中随机抽取了100名火炬手进行信息分析,得到如下表格:
年龄
性别 总计
满50周岁 未满50周岁
男 15 45 60
女 5 35 40
总计 20 80 100
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
根据小概率值的独立性检验,试判断全省火炬手的性别与年龄满或未满50周岁是否有关联;
(2)在全省的火炬手中,男性占比72%,女性占比28%,且50%的男性火炬手和25%的女性火炬手喜欢观看
足球比赛.某电视台随机选取一位喜欢足球比赛的火炬手做访谈,请问这位火炬手是男性的概率为多少?
【答案】(1)全省火炬手性别与年龄满或未满50周岁相互独立(没有关联)
(2)
【分析】(1)根据列联表中的数据,求得的值,结合附表,即可得到结论;
(2)设表示火炬手为男性,表示火炬手喜欢足球,结合条件概率和全概率公式,即可求解.
【详解】(1)解:零假设为::全省火炬手性别与年龄满或未满50周岁相互独立(没有关联),
根据列联表中的数据,计算得,
所以根据小概率值的独立性检验,没有充分证据推断不成立,
因此可以认定为成立,
全省火炬手性别与年龄满或未满50周岁相互独立(没有关联).(2)解:设表示火炬手为男性,表示火炬手喜欢足球,
则,
所以这位火炬手是男性的概率约为.
20.如图,在直三棱柱中,,,D为的中点.
(1)证明:;
(2)若点到平面的距离为,求平面与平面的夹角的正弦值.
【答案】(1)证明见解析
(2).
【分析】(1)由平面平面,得平面,得,
又因得平面,进而可证;
(2)由向量法先根据到平面的距离为,求出的坐标,再由向量法求平面与平面的夹角.
【详解】(1)
连接,
因为四边形为正方形,所以.
在直三棱柱中,平面平面,
由得,又平面平面,
所以平面,又平面,所以,又,平面,平面,
所以平面,又平面,
所以.
(2)以为原点,,,所在直线分别为,,轴建立如图所示的空间直角坐标系,
设,则,,,,
,,.
设为平面ABD的一个法向量,
则,即,得,令,则,
故,
由题意,,解得,
所以,.
设为平面BCD的一个法向量,
则,即,
令,则,,即,
平面ABC的一个法向量为,
设平面和平面的夹角为,
则,
所以,
所以平面和平面的夹角的正弦值为.
21.已知双曲线,直线过双曲线的右焦点且交右支于两点,点为线段的中点,点在轴上,.
(1)求双曲线的渐近线方程;
(2)若,求直线的方程.
【答案】(1)
(2)或或【分析】(1)根据等轴双曲线方程即可求解渐近线方程,
(2)联立直线与双曲线方程得韦达定理,即可根据向量数量积的几何意义将其转化为,由坐标运算即可
求解.
【详解】(1)由题知,,所以双曲线的渐近线方程为.
(2)双曲线的右焦点坐标为,
由题知,直线AB的斜率不为0,设直线方程为,代入双曲线中,
化简可得:,
设,则.
则
∴线段中点的坐标为,
直线方程为.
(i)当时,点恰好为焦点,此时存在点或,使得.
此时直线方程为.
(ii)当时,令可得,可得点的坐标为,
由于所以,
由,即,也即:.
化简可得,解出,
由于直线要交双曲线右支于两点,所以,即,故舍去.
可得直线的方程为.
综上:直线方程为或或.
22.已知函数.
(1)若函数在点处的切线与函数的图象有公共点,求实数的取值范围;
(2)若函数和函数的图象没有公共点,求实数的取值范围.
【答案】(1)
(2)【分析】(1)求导,即可根据点斜式求解切线方程,联立方程转化为一元二次方程,利用判别式即可求
解,
(2)将问题转化为没有实数根,求导,利用导数确定函数的单调性,分类讨论,进而结合零点存在性定理
即可求解.
【详解】(1)因为,所以,
则在点处的切线斜率为,
所以切线方程为,即.
由得,即.
因为函数定义域为,所以方程有非零实数根,
当时,,符合题意,当时,则,即,且,
所以实数a的取值范围是.
(2)因为函数和函数的图象没有公共点,所以,即无实根,
所以当时,无实根,
因为,即是偶函数,所以在上无实根.
,
记则,.
①当时,,又,则,所以,满足在上无实根.
②当时,在上有实根,不合题意,舍去.
③当时,,所以在单调递增,
则,所以在上单调递增,
所以,满足在上无实根.
④当时,因为在单调递增,且,,
则存在唯一的,使,列表得
- 0 +
↘ 极小值 ↗
所以当时,,则在单调递减,则,
又因为,且在上连续,
所以在上有实根,不合题意.
综上可知,实数的取值范围是.【点睛】方法点睛:
1. 导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.
注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问
题处理.
2.利用导数解决含参函数的单调性问题时,一般将其转化为不等式恒成立问题,解题过程中要注意分类讨
论和数形结合思想的应用.
3.证明不等式,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这
种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.