文档内容
专题5.1 导数的概念及其意义
知识储备
1.导数的概念
一般地,函数y=f(x)在x=x 处的瞬时变化率 为函数y=f(x)在x
0
=x 处的导数,记作f′(x)或y′ 即f′x= .
0 0 0
称函数f′(x)= 为f(x)的导函数.
2.导数的几何意义
函数f(x)在点x 处的导数f′(x)的几何意义是在曲线y=f(x)上点P(x ,f(x))处的切线的斜率.相应
0 0 0 0
地,切线方程为 y - f ( x ) = f ′ ( x )( x - x ) .
0 0 0
能力检测
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字
笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、单选题
1.(2020·全国高二课时练习)甲、乙两厂污水的排放量W与时间 的关系如图所示,则治污效果
较好的是( )
A.甲厂 B.乙厂 C.两厂一样 D.不确定
【答案】B
【解析】在 处,虽然有 ,但 ,
所以在相同时间 内,甲厂比乙厂的平均治污率小,所以乙厂治污效果较好.故选:B.
2.(2020·全国高二课时练习)已知函数 和 在区间 上的图象如图所示,则下列说法正确的是( )
A. 在a到b之间的平均变化率大于 在a到b之间的平均变化率
B. 在a到b之间的平均变化率小于 在a到b之间的平均变化率
C.对于任意 ,函数 在 处的瞬时变化率总大于函数 在 处的瞬时
变化率
D.存在 ,使得函数 在 处的瞬时变化率小于函数 在 处的瞬时变
化率
【答案】D
【解析】∵ 在a到b之间的平均变化率是 ,
在a到b之间的平均变化率是 ,
又 , ,
∴ ,
∴A、B错误;
易知函数 在 处的瞬时变化率是函数 在 处的导数,
即函数 在该点处的切线的斜率,
同理可得:函数 在 处的瞬时变化率是函数 在该点处的导数,即函数 在该点处的切线的斜率,由题中图象可知:
时,函数 在 处切线的斜率有可能大于 在 处切线的斜率,也有可
能小于 在 处切线的斜率,故C错误,D正确.故选:D.
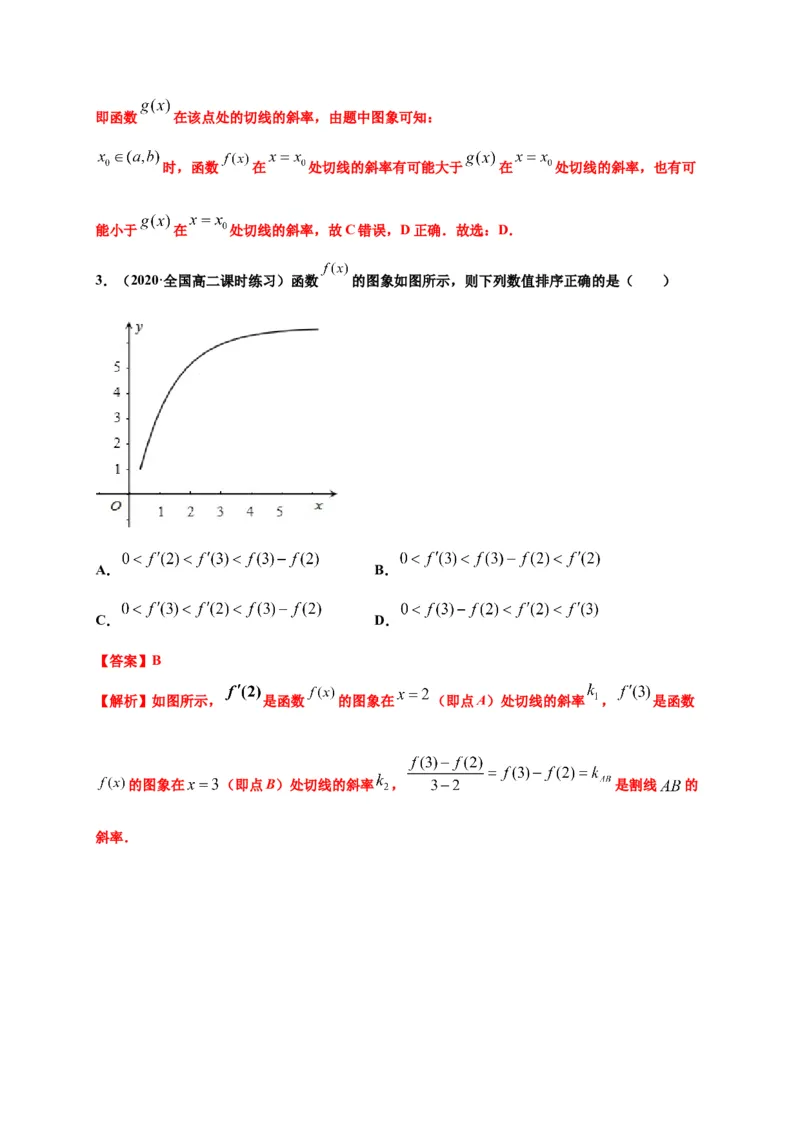
3.(2020·全国高二课时练习)函数 的图象如图所示,则下列数值排序正确的是( )
A. B.
C. D.
【答案】B
【解析】如图所示, 是函数 的图象在 (即点A)处切线的斜率 , 是函数
的图象在 (即点B)处切线的斜率 , 是割线 的
斜率.由图象知, ,即 .故选:B.
4.(2020·全国高二课时练习)函数 在 处的导数 的几何意义是( )
A.在点 处与 的图象只有一个交点的直线的斜率
B.过点 的切线的斜率
C.点 与点 的连线的斜率
D.函数 的图象在点 处的切线的斜率
【答案】D
【解析】 的几何意义是函数 的图象在点 处的切线的斜率.故选:D.
5.(2020·全国高二课时练习)某物体的运动方程为 (位移单位:m,时间单位:s),若
,则下列说法中正确的是( )
A. 是物体从开始到 这段时间内的平均速度
B. 是物体从 到 这段时间内的速度
C. 是物体在 这一时刻的瞬时速度D. 是物体从 到 这段时间内的平均速度
【答案】C
【解析】 是物体在 这一时刻的瞬时速度.故选:C.
6.(2020·全国高二课时练习)一质点的运动方程是 ,则在时间 内相应的平均
速度为( )
A. B. C. D.
【答案】D
【解析】 .故选:D.
7.(2020·全国高二课时练习)已知某质点的运动方程为 ,其中s的单位是m,t的单位
是s,则该质点在 末的瞬时速度为( )
A. B. C. D.
【答案】C
【解析】 ,
所以该质点在 末的瞬时速度为 .故选:C.
8.(2020·全国高二课时练习)某质点的运动规律为 ,则在时间 内,质点的位
移增量等于( )
A. B. C. D.
【答案】A
【解析】位移增量 .故选:A.二、多选题
9.(2020·全国高二课时练习)(多选)已知函数 的定义域为R,其导函数 的图象如图
所示,则对于任意 ,下列结论正确的是( )
A. B.
C. D.
【答案】AD
【解析】由题中图象可知,导函数 的图象在x轴下方,即 ,且其绝对值越来越小,
因此过函数 图象上任一点的切线的斜率为负,并且从左到右切线的倾斜角是越来越大的钝角,
由此可得 的大致图象 如图所示.
A选项表示 与 异号,即 图象的割线斜率 为负,故A正确;B选项表示 与 同号,即 图象的割线斜率 为正,故B
不正确; 表示 对应的函数值,即图中点B的纵坐标, 表示当
和 时所对应的函数值的平均值,即图中点A的纵坐标,显然有
,故C不正确,D正确.故选:AD.
10.(2020·全国高二课时练习)(多选)下列命题正确的是( )
A.若 ,则函数 在 处无切线
B.函数 的切线与函数的图象可以有两个公共点
C.曲线 在 处的切线方程为 ,则当 时,
D.若函数 的导数 ,且 ,则 的图象在 处的切线方程为
【答案】BD
【解析】若 ,则函数 在 处的切线斜率为0,故选项 错误;
函数 的切线与函数的图象可以有两个公共点,例如函数 ,在 处的切
线为 ,与函数的图象还有一个公共点 ,故选项 正确;
因为曲线 在 处的切线方程为 ,所以又 ,故选项 错误;
因为函数 的导数 ,所以 ,又 ,所以切点坐标为
,斜率为 ,所以切线方程为 ,化简得 ,故选项 正确.故选:
BD.
11.(2020·无锡市第一中学高三月考)为满足人民对美好生活的向往,环保部门要求相关企业加
强污水治理,排放未达标的企业要限期整改、设企业的污水排放量W与时间t的关系为 ,
用 的大小评价在 这段时间内企业污水治理能力的强弱,已知整改期内,甲、
乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论,其中正确结论为( )
A.在 这段时间内,甲企业的污水治理能力比乙企业强;
B.在 时刻,甲企业的污水治理能力比乙企业强;
C.在 时刻,甲、乙两企业的污水排放都已达标;
D.甲企业在 这三段时间中,在 的污水治理能力最强.
【答案】ABC
【解析】 表示区间端点连线斜率的负数,
在 这段时间内,甲的斜率比乙的小,所以甲的斜率的相反数比乙的大,因此甲企业的污水治理能力比乙企业强;A正确;
甲企业在 这三段时间中,甲企业在 这段时间内,甲的斜率最小,其相反
数最大,即在 的污水治理能力最强.D错误;
在 时刻,甲切线的斜率比乙的小,所以甲切线的斜率的相反数比乙的大,甲企业的污水治理能力
比乙企业强;B正确;
在 时刻,甲、乙两企业的污水排放量都在污水打标排放量以下,所以都已达标;C正确;
故选:ABC.
12.(2020·长沙市·湖南师大附中高二期末)若直线 与曲线 满足下列两个条件:①直线 在点
处与曲线 相切;②曲线 在点 附近位于直线 的两侧,则称直线 在点 处“切过”
曲线 .则下列结论正确的是( )
A.直线 在点 处“切过”曲线
B.直线 在点 处“切过”曲线
C.直线 在点 处“切过”曲线
D.直线 在点 处“切过”曲线
【答案】ACD
【解析】A项,因为 ,当 时, ,
所以 是曲线 在点 处的切线.
当 时, ;当 时, ,
所以曲线 在点 附近位于直线 的两侧,结论正确;B项, ,当 时, ,在 处的切线为 .
令 ,则 ,
当 时, ;当 时, ,
所以 .故 ,
即当 时,曲线 全部位于直线 的下侧(除切点外),结论错误;
C项, ,当 时, ,在 处的切线为 ,
由正弦函数图像可知,曲线 在点 附近位于直线 的两侧,结论正确;
D项, ,当 时, ,在 处的切线为 ,
由正切函数图像可知,曲线 在点 附近位于直线 的两侧,结论正确.故选:ACD.
三、填空题
13.(2020·全国高二课时练习)设函数 为可导函数,且满足 ,
则曲线 在点 处切线的倾斜角为_________.
【答案】120°
【解析】∵
,
∴ ,即 .
曲线在点 处切线的斜率 ,
所以倾斜角为120°.故答案为:120°.
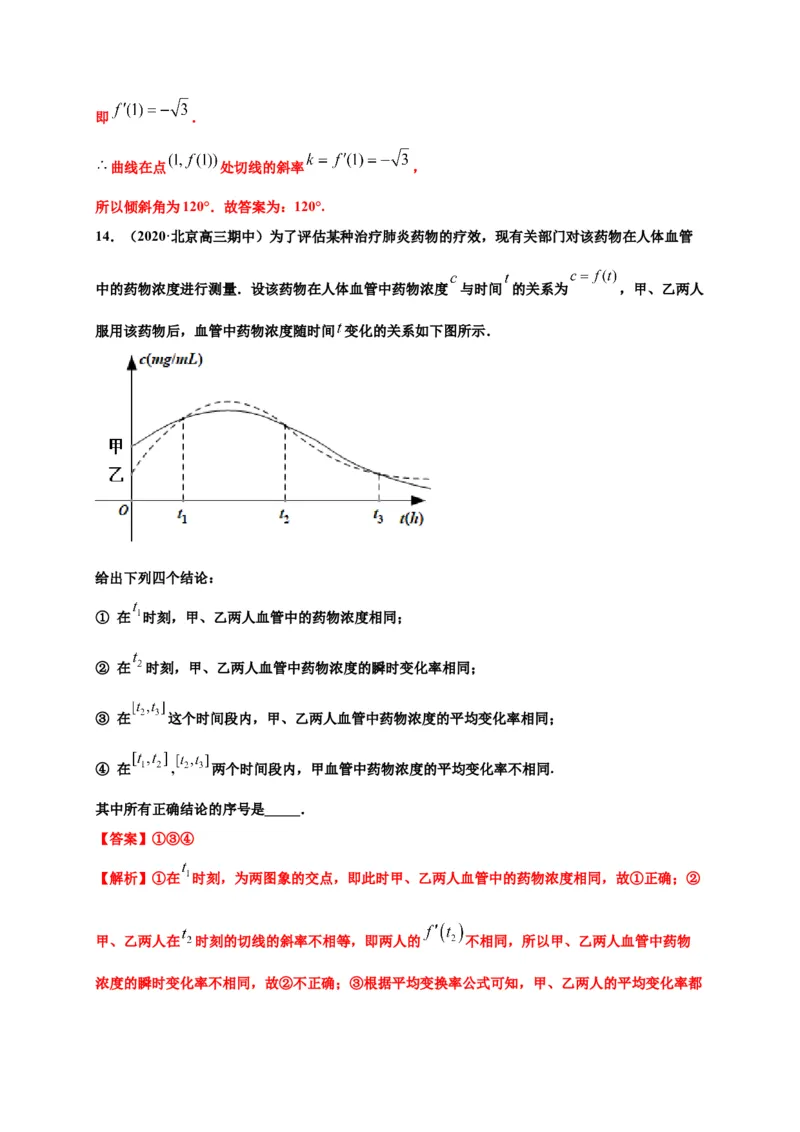
14.(2020·北京高三期中)为了评估某种治疗肺炎药物的疗效,现有关部门对该药物在人体血管
中的药物浓度进行测量.设该药物在人体血管中药物浓度 与时间 的关系为 ,甲、乙两人
服用该药物后,血管中药物浓度随时间 变化的关系如下图所示.
给出下列四个结论:
① 在 时刻,甲、乙两人血管中的药物浓度相同;
② 在 时刻,甲、乙两人血管中药物浓度的瞬时变化率相同;
③ 在 这个时间段内,甲、乙两人血管中药物浓度的平均变化率相同;
④ 在 , 两个时间段内,甲血管中药物浓度的平均变化率不相同.
其中所有正确结论的序号是_____.
【答案】①③④
【解析】①在 时刻,为两图象的交点,即此时甲、乙两人血管中的药物浓度相同,故①正确;②
甲、乙两人在 时刻的切线的斜率不相等,即两人的 不相同,所以甲、乙两人血管中药物
浓度的瞬时变化率不相同,故②不正确;③根据平均变换率公式可知,甲、乙两人的平均变化率都是 ,故③正确;④在 时间段,甲的平均变化率是 ,在 时
间段,甲的平均变化率是 ,显然不相等,故④正确.故答案为:①③④
15.(2020·全国高三月考)若曲线 在点 处的切线也是曲
线 的切线,则 ______.
【答案】
【解析】由已知得 ,所以 , ,所以切线方程为
.由 得 ,令 ,解得
.代入切线 ,求得切点为 , .
将切点坐标代入曲线 ,求得 .故答案为:
四、双空题
16.(2020·全国高二课时练习)过曲线 上两点 和 作曲线的割线,
当 时,割线的斜率为________;当 时,割线的斜率为________.
【答案】2.1 2.001
【解析】∵ ,∴ ,∴割线斜率为 ,当 时,割线 的斜率为 .
当 时,割线 的斜率为 .故答案为:2.1;2.001.