5.2三角函数的概念（解析版）_E015高中全科试卷_数学试题_必修1_02.同步练习_4.同步练习（第四套）_5.2三角函数的概念

5.2三角函数的概念 主要命题方向 1. 利用三角函数的定义求三角函数值；2. 三角函数在各象限内符号的应用；3. 诱导公式(一)的应用；4. 分类讨论思想的应用；5. 根据同角三角函数关系求值；6. 弦化切求值；7. 化简三角函数式； 8. 三角恒 等式的证明；9. sinθ±cosθ，sinθ·cosθ三者的关系及方程思想的运用. 配套提升训练 一、单选题 1．（2020·阜新市第二高级中学高一期末）已知角α终边过点P(1，-1)，则tan α的值为（ ） A．1 B．-1 C． D． 【答案】B 【解析】 ∵ 角α终边过点P(1，-1)， ∴ ， 故选：B. 2．（2020·阜新市第二高级中学高一期末）若 ，则 在（ ） A．第一、二象限 B．第一、三象限 C．第一、四象限 D．第二、四象限 【答案】B 【解析】 设 是 角终边上任意一点（异于原点）， ， 即 与 同号，则 在第一、三象限 故选：B3．（2020·辽宁大连�高一期末）若 ，则点 位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】C 【解析】 由 知： ∴ ， 故，P位于第三象限 故选：C 1 4．已知α是第三象限的角,若tanα= ,则cosα=（ ） 2 √5 2√5 √5 2√5 A. - B. - C. D. 5 5 5 5 【答案】B 1 sinα 1 2√5 【解析】tanα= , = ,cosα=2sinα ,sin2α+cos2α=1,解方程组得：cosα=- ，选B. 2 cosα 2 5 P3a,4aa 0  sin 5．若角 终边经过点 ,则 （ ） 3 4 3 4   A. 5 B. 5 C. 5 D. 5 【答案】D 4a 4 sin  r  9a2 16a2 5 a 5 a 5 【解析】 , ,选D. 6．（2020·四川武侯�成都七中高三其他（理））记 ，那么 （ ） A． B． C． D． 【答案】B 【解析】, ,从而 ， ， 那么 ， 故选B． 7．（2020·永州市第四中学高一月考）若一个 角的终边上有一点 且 ，则 的值为( ) A． B． C．－4 或 D． 【答案】C 【解析】 由已知，得 ，解得 或 ， 故选C． 1 sincos 8.已知2， 5，则tan等于（ ） 3 3 4 3 4 3    A. 4 B. 4 或 3 C. 4 或3 D. 5 【答案】A 【解析】 1 sincos ∵2， 5，1 12 12sincos sincos 0 ∴平方可得 25，即 25 ， ∴sin0，cos0， 2 1  4 3 ∵ 可得： cos  cos21 ，解得： cos ，或  （舍去）， sin2cos21 5  5 5 1 4 3 3 sin   tan ∴ 5 5 5，可得： 4 ． 故选：A． 9．（2020·永州市第四中学高一月考）点P从 点出发，沿单位圆 逆时针方向运动 弧长 到达Q点，则Q点坐标为（ ） A． B． C． D． 【答案】A 【解析】 由题意可知 ， 根据三角函数的定义可知 ， ， 所以点 的坐标是 . 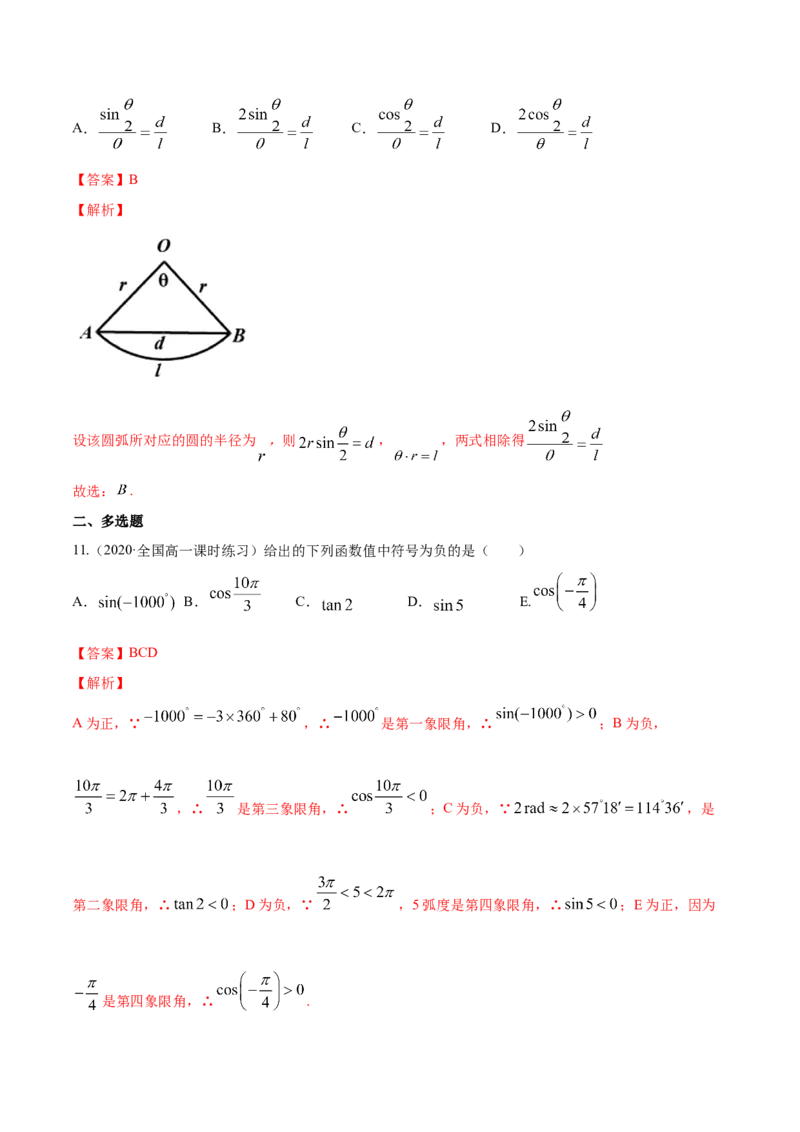故选：A 10．（2020·安徽高三月考（文））达芬奇的经典之作《蒙娜丽莎》举世闻名，画中女子神秘的微笑，数百 年来让无数观赏者入迷，现将画中女子的嘴唇近似的看作一个圆弧，设嘴角 、 间的圆弧长为 ，嘴角 间的距离为 ，圆弧所对的圆心角为 （ 为弧度角），则 、 和 所满足的恒等关系为（ ）A． B． C． D． 【答案】B 【解析】 设该圆弧所对应的圆的半径为 ，则 ， ，两式相除得 故选： . 二、多选题 11.（2020·全国高一课时练习）给出的下列函数值中符号为负的是（ ） A． B． C． D． E. 【答案】BCD 【解析】 A为正，∵ ，∴ 是第一象限角，∴ ；B为负， ，∴ 是第三象限角，∴ ；C为负，∵ ，是 第二象限角，∴ ；D为负，∵ ，5弧度是第四象限角，∴ ；E为正，因为 是第四象限角，∴ .故选：BCD. 12．（2020·山东临沂�高一期末）对于① ，② ，③ ，④ ，⑤ ，⑥ ，则 为第二象限角的充要条件为（ ） A．①③ B．①④ C．④⑥ D．②⑤ 【答案】BC 【解析】 若 为第二象限角，则 ， ， . 所以， 为第二象限角 或 或 . 故选：BC. 13．设角 的终边上一点P的坐标是 ，则 的值不可能为（ ）、 A． B． C． D． 【答案】ABC 【解析】 因为角 的终边上一点P的坐标是 ， 则 ， ， 所以角 第一象限角， 所以 ， 所以 ， ， 当 时， 为第一象限的角， 所以 的值可能为 ，和 不可能为 的值， 而 不是第一象限的角． 所以A，B，C都不能取到． 故选：ABC． 14．（2020·山东省微山县第一中学高一月考）已知 ， ，则下列结论正确的是 （ ） A． B． C． D． 【答案】ABD 【解析】 ① 即 ，② ①加②得 ①减②得 综上可得，正确的有 故选： 三、填空题 15．（2020·全国高一课时练习）若角α的终边上有一点P（－4，a），且sinα·cosα＝ ，则a的值为 ； 【答案】 或 【解析】 根据三角函数的定义， ， ，所以根据已知条件， ，所 以解得： 或 sin2cos 5 tan 16．若 ，则 ______. 1  【答案】 2 sin2cos 5 sin24sincos4cos25(sin2cos2) 【解析】将 两边平方可得 ,即1 tan  4sin24sincoscos20 ,即 4tan24tan10 ,故 (2tan1)2 0 ,即 2 , 故应选D. 2 sin2cos 17．已知  是第一象限角，若 5 ，则 sincos ______________. 7 【答案】5 2 2 8 21 sin2cos （2cos ）2 cos21 5cos2 cos 0 【解析】∵ 5 ，则 5 ，∴ 5 25 ，即  3 7 3 4  cos  5cos  0 cos sin  5 5 ，又∵  为第一象限的角，∴ 5 ， 5，从而 7 7 sincos 5 ，故答案为5 . 四、双空题 18．（2020·浙江衢州�高一期末）已知角 的终边过点 ，则 ________， ________. 【答案】 【解析】 角 的终边过点 ，则 ， ， ，故答案为： ； ． 19．（2018·浙江丽水�高一期末）在平面直角坐标系中，角 的顶点与原点重合，始边与 轴的非负半轴 重合，终边过点 ，则 _______； _______. 【答案】 【解析】 ∵角 终边过点 ， ， ∴ ， ， ， ∴ . 故答案为： ； . 20．（2020·浙江丽水�高一期中）已知点 是角 终边上的一点，则 =______， =_______. 【答案】 【解析】 根据题意知： ， . 故答案为：-2；4. 21．（2020·上海高一课时练习）若 ，则 ___________； __________.【答案】 【解析】 因为 ，所以 ，所以 ， . 故答案为： ； 五、解答题 22．（2020·内蒙古集宁一中高一期末（理））已知角 的终边经过点 ，且 ． （1）求 的值； （2）求 的值． 【答案】（1） ；（2） 【解析】 （ ）因为已知角 的终边经过点 ，且 ，所以有 ，求得 ； 1 （ ）由（ ）可得， ， 2 1 原式 ． = = = 23．（2020·浙江高一课时练习）若已知角 终边上一点 ，且 ，能否求出 的值？若能，求出其值；若不能，请说明理由．【答案】能，见解析 【解析】 能求出 ， 的值． 因为角 的终边过点 ， 所以 ． 因为 ，所以 或 ． ①当 时，点P的坐标为 ，角 为第一象限角， 此时 ； ②当 时，点P的坐标为 ，角 为第二象限角， 此时 ． 24.（甘肃省宁县第二中学2019年高一下期中） 1sincos2sincos  求证： 1sincos sinα+cosα． 【答案】见证明 【解析】 sincos2 证明：∵1+2sinα•cosα＝ ∵1+sinα+cosα≠0， 1sincos2sincos ∴左端 1sincos sincossincos2  1sincos sincos1sincos  1sincos＝sinα+cosα＝右端． 1sincos2sincos sincos ∴ 1sincos 25．（2020·山西应县一中高一期中（理））已知 ，求下列各式的值. （1） ； （2） . 【答案】（1） ；（2） ． 【解析】 由 ，解得 ． （1） ； （2） ． 26．（2020·全国高一课时练习）在平面直角坐标系中，角α的终边在直线3x＋4y＝0上，求sinα－3cosα＋ tanα的值. 【答案】－ 或 . 【解析】当角α的终边在射线y＝－ x(x>0)上时，取终边上一点P(4，－3)， 所以点P到坐标原点的距离r＝|OP|＝5， 所以sinα＝ ＝ ＝－ ，cosα＝ ＝ ， tanα＝ ＝－ . 所以sinα－3cosα＋tanα＝－ － － ＝－ . 当角α的终边在射线y＝－ x(x<0)上时，取终边上一点P′(－4，3)， 所以点P′到坐标原点的距离r＝|OP′|＝5， 所以sinα＝ ＝ ，cosα＝ ＝－ ， tanα＝ ＝－ . 所以sinα－3cosα＋tanα＝ －3× － ＝ ＋ － ＝ . 综上，sinα－3cosα＋tanα的值为－ 或 . 27．（2020·永州市第四中学高一月考）已知 .试用k表示 的值. 【答案】详见解析 【解析】， , 当 时， ，此时 ， 当 时， ，此时 .