东北三省三校（哈师大附中、东北师大附中、辽宁省实验中学）2023-2024学年高三下学期第一次联合模拟考数学试卷(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集

哈尔滨师大附中 东北师大附中 辽宁省实验中学 2024 年高三第一次联合模拟考试 数学 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上． 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑动，用橡 皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，定在．本试卷上 无效． 3．考试结束后，将本试卷和答题卡一并交回． 一、单项选择题：本大题共 8小题，每小题 5分，共 40分．在每小题给出的四选项中，只有 一项是符合题目要求的． 1．已知集合M ={ 1,2 }，N = { x∈R log ( 2x−1 )≤2 } ，则M N =（ ） 2 A．{ 1 } B．{ 2 } C．{ 1,2 } D．∅ 2．已知复数z的共轭复数是z，若z⋅i=1−i，则z =（ ） A．−1+i B．−1−i C．1−i D．1+i a 3．已知函数y = f ( x )是定义在R上的奇函数，且当x<0时， f ( x )= x2 + ，若 f ( 3 )=−8，则a= x （ ） 1 1 A．−3 B．3 C． D．− 3 3 x2 y2 4．已知平面直角坐标系xOy中，椭圆C： + =1（a>b>0）的左顶点和上顶点分别为A，B，过 a2 b2   左焦点F 且平行于直线AB的直线交y轴于点D，若OD=2DB，则椭圆C的离心率为（ ） 1 3 1 2 A． B． C． D． 2 2 3 3  2x 5．1−  ( x− y )5的展开式中x3y2的系数为（ ）  y  A．55 B．−70 C．30 D．−25 64 6．已知正四棱锥P−ABCD各顶点都在同一球面上，且正四棱锥底面边长为4，体积为 ，则该球表面积 3 为（ ） 4π A．9π B．36π C．4π D． 3 学科网（北京）股份有限公司7．已知函数 f ( x )=e2x −e−2x −ax，若x≥0时，恒有 f ( x )≥0，则a的取值范围是（ ） A．(−∞,2 ] B．(−∞,4 ] C．[ 2,+∞) D．[ 4,+∞) 10 11 ln2.2 8．设a =e33，b=ln ，c= ，则（ ） 10 10 A．a0，则下列命题正确的是（ ） n 1 A．若a +a =4，则S =18 3 7 9 B．若S >0，S <0，则a2 >a2 15 16 8 9 C．若a +a =1，a +a =9，则a +a =25 1 2 3 4 7 8 D．若a =S ，则S >0，S <0 8 10 9 10 10．在平面直角坐标系xOy中，抛物线C：y2 =4x的焦点为F ，点P在抛物线C上，点Q在抛物线C的 准线上，则以下命题正确的是（ ） A． PQ + PF 的最小值是2 B． PQ ≥ PF   C．当点P的纵坐标为4时，存在点Q，使得QF =3FP D．若△PQF是等边三角形，则点P的橫坐标是3 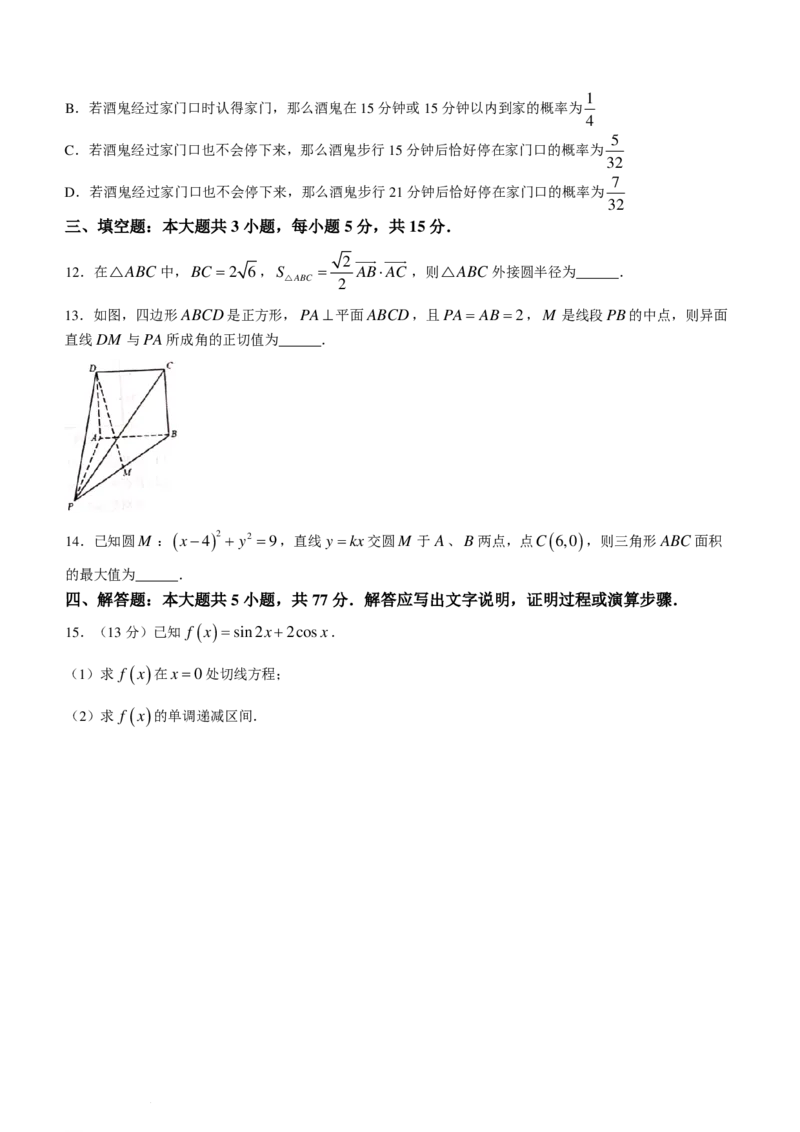11．在一个只有一条环形道路的小镇上，有2家酒馆A，一个酒鬼家住在D，其相对位置关系如图所示．小 镇的环形道路可以视为8段小路，每段小路需要步行3分钟时间．某天晚上酒鬼从酒馆喝完酒后离开，因为 醉酒，所以酒鬼在每段小路的起点都等可能的选择顺时针或者逆时针的走完这段小路。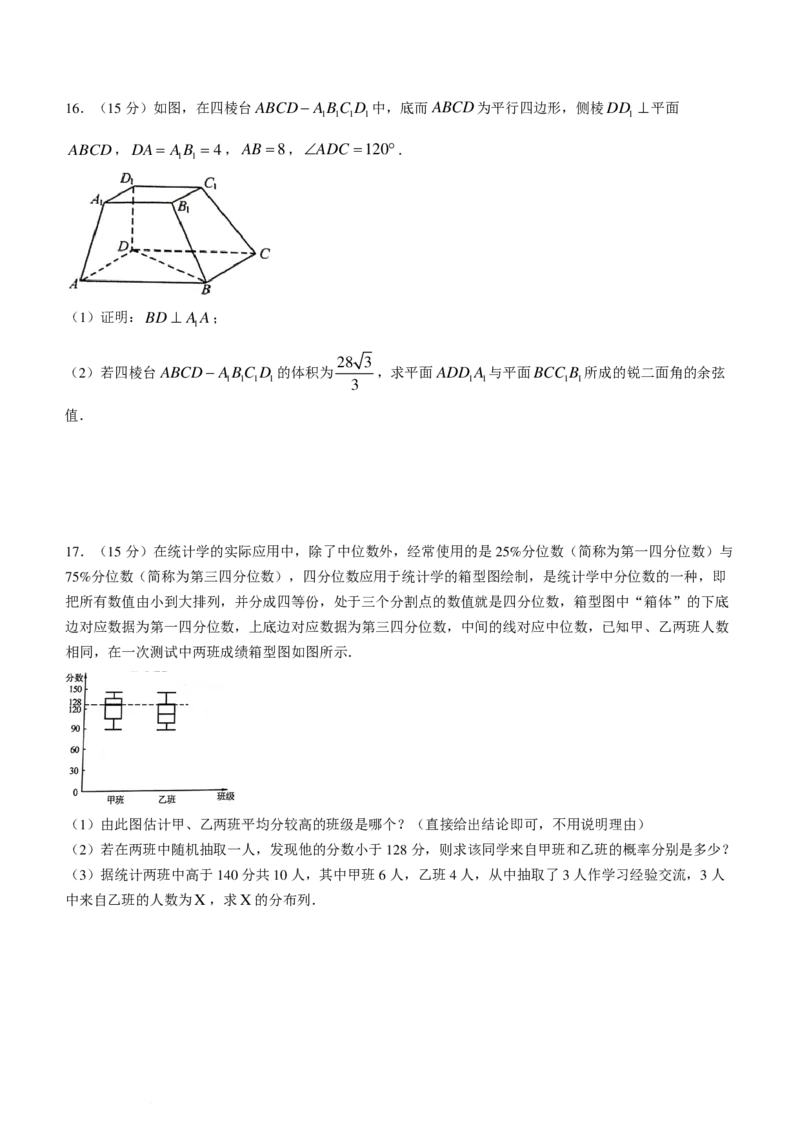下述结论正确的是 （ ） 1 A．若酒鬼经过家门口时认得家门，那么酒鬼在10分钟或10分钟以内到家的概率为 8 学科网（北京）股份有限公司1 B．若酒鬼经过家门口时认得家门，那么酒鬼在15分钟或15分钟以内到家的概率为 4 5 C．若酒鬼经过家门口也不会停下来，那么酒鬼步行15分钟后恰好停在家门口的概率为 32 7 D．若酒鬼经过家门口也不会停下来，那么酒鬼步行21分钟后恰好停在家门口的概率为 32 三、填空题：本大题共 3小题，每小题 5分，共 15分．   2 12．在△ABC中，BC =2 6，S = AB⋅AC ，则△ABC外接圆半径为______． △ABC 2 13．如图，四边形ABCD是正方形，PA⊥平面ABCD，且PA= AB=2，M 是线段PB的中点，则异面 直线DM 与PA所成角的正切值为______． 14．已知圆M ：( x−4 )2 + y2 =9，直线y =kx交圆M 于A、B两点，点C ( 6,0 )，则三角形ABC面积 的最大值为______． 四、解答题：本大题共 5小题，共 77分．解答应写出文字说明，证明过程或演算步骤． 15．（13分）已知 f ( x )=sin2x+2cosx． （1）求 f ( x )在x=0处切线方程； （2）求 f ( x )的单调递减区间． 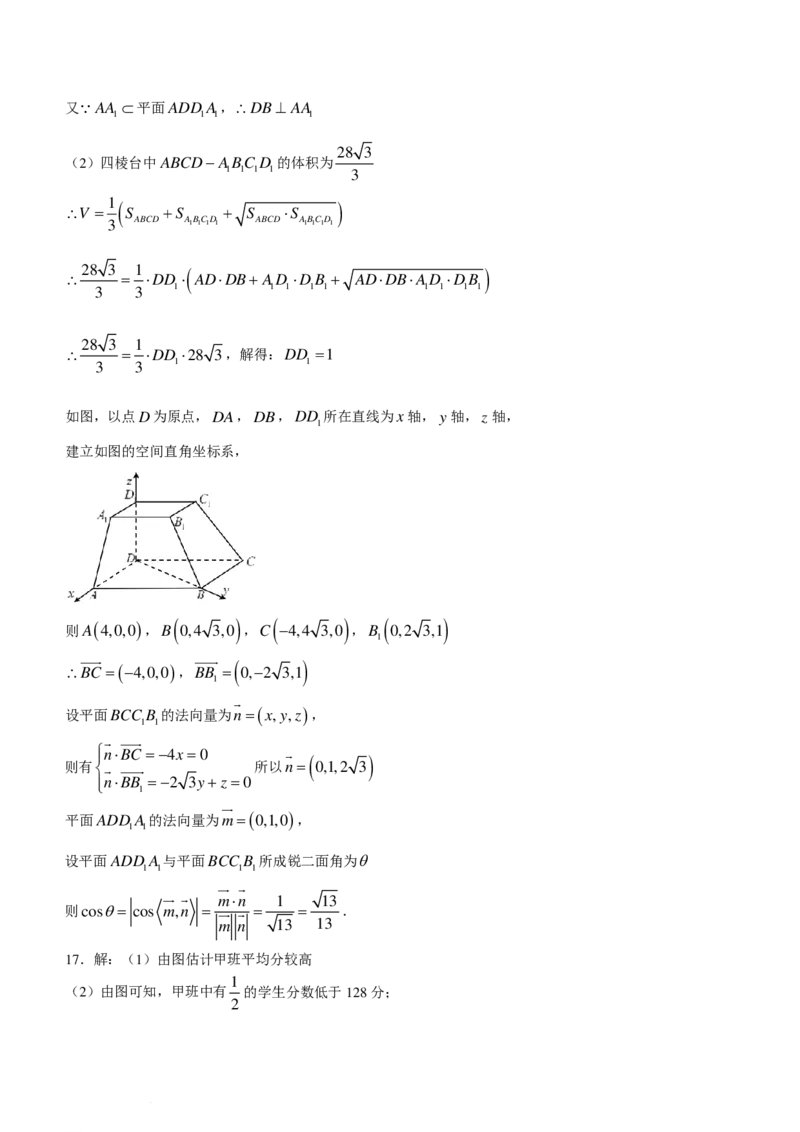学科网（北京）股份有限公司16．（15分）如图，在四棱台ABCD−ABC D 中，底而ABCD为平行四边形，侧棱DD ⊥平面 1 1 1 1 1 ABCD，DA= AB =4，AB=8，∠ADC =120°． 1 1 （1）证明：BD⊥ AA； 1 28 3 （2）若四棱台ABCD−ABC D 的体积为 ，求平面ADD A与平面BCC B 所成的锐二面角的余弦 1 1 1 1 3 1 1 1 1 值． 17．（15分）在统计学的实际应用中，除了中位数外，经常使用的是25%分位数（简称为第一四分位数）与 75%分位数（简称为第三四分位数），四分位数应用于统计学的箱型图绘制，是统计学中分位数的一种，即 把所有数值由小到大排列，并分成四等份，处于三个分割点的数值就是四分位数，箱型图中“箱体”的下底 边对应数据为第一四分位数，上底边对应数据为第三四分位数，中间的线对应中位数，已知甲、乙两班人数 相同，在一次测试中两班成绩箱型图如图所示． （1）由此图估计甲、乙两班平均分较高的班级是哪个？（直接给出结论即可，不用说明理由） （2）若在两班中随机抽取一人，发现他的分数小于128分，则求该同学来自甲班和乙班的概率分别是多少？ （3）据统计两班中高于140分共10人，其中甲班6人，乙班4人，从中抽取了3人作学习经验交流，3人 中来自乙班的人数为X，求X的分布列． 学科网（北京）股份有限公司x2 y2 18．（17分）已知双曲线C： − =1（a>0，b>0）的右顶点E ( 1,0 )，斜率为1的直线交C于 a2 b2 M 、N 两点，且MN 中点Q ( 1,3 )． （1）求双曲线C的方程； （2）证明：△MEN为直角三角形； （3）若过曲线C上一点P作直线与两条渐近线相交，交点为A，B，且分别在第一象限和第四象限，若   1  AP=λPB，λ∈ ,2 ，求△AOB面积的取值范围．   3  19．（17分）十七世纪至十八世纪的德国数学家莱布尼兹是世界上第一个提出二进制记数法的人，用二进制 记数只需数字0和1，对于整数可理解为逢二进一，例如：自然数1在二进制中就表示为( 1 ) ，2表示为 2 ( 10 ) ，3表示为( 11 ) ，5表示为( 101 ) ，发现若n∈N 可表示为二进制表达式( a aa ⋅⋅⋅a a ) ，则 2 2 2 + 0 1 2 k−1 k 2 n=a ⋅2k +a ⋅2k−1+⋅⋅⋅+a ⋅21+a ，其中a =1，a =0或1（i =1,2,⋅⋅⋅k）． 0 1 k−1 k 0 i （1）记S ( n )=a +a +⋅⋅⋅+a +a ，求证S ( 8n+3 )=S ( 4n+3 )； 0 1 k−1 k （2）记I ( n )为整数n的二进制表达式中的0的个数，如I ( 2 )=1，I ( 3 )=0． （ⅰ）求I ( 60 )； 511 （ⅱ）求∑2I(n) （用数字作答）． n=1 学科网（北京）股份有限公司2024 年高三第一次联合模拟考试数学 参考答案 一、单项选择题 1-4 CABD 5-8 CBBB 二、多项选择题 9．ACD 10．ABD 11．ABD 三、填空题 27 12．3 13． 5 14． 4 四、解答题 15．解：（1） f′( x )=2cos2x−2sinx f′( 0 )=2， f ( 0 )=2 ∴ f ( x )在x=0处的切线方程为y−2=2 ( x−0 )，即y =2x+2 （2） f′( x )=2cos2x−2sinx=2 ( 1−sin2 x ) −2sinx=−2 ( 2sin2 x+sinx−1 ) f′( x )<0则−2 ( 2sin2 x+sinx−1 ) <0 即−2 ( 2sinx−1 )( sinx+1 )<0 1  π 5π 即sinx> 解得x∈ 2kπ+ ,2kπ+  ，k∈Z 2  6 6   π 5π 故 f ( x )的单调递减区间为 2kπ+ ,2kπ+  ，k∈Z  6 6  16．解：（1）底面ABCD为平行四边形， ∠ADC =120°，∴∠DAB=60°． DA=4，AB=8 由余弦定理可得：DB2 = AB2 + AD2 −2AB×ADcos60°=48，∴DB=4 3 则DA2 +DB2 = AB2，∴DA⊥ DB 侧棱DD ⊥平面ABCD，DB⊂平面ABCD，∴DD ⊥ DB 1 1 又DA⊂平面ADD A，DD ⊂平面ADD A，且DADD = D 1 1 1 1 1 1 ∴DB ⊥平面ADD A 1 1 学科网（北京）股份有限公司又AA ⊂平面ADD A，∴DB⊥ AA 1 1 1 1 28 3 （2）四棱台中ABCD−ABC D 的体积为 1 1 1 1 3 1( ) ∴V = S +S + S ⋅S 3 ABCD A 1 B 1 C 1 D 1 ABCD A 1 B 1 C 1 D 1 28 3 1 ( ) ∴ = ⋅DD ⋅ AD⋅DB+ AD ⋅DB + AD⋅DB⋅AD ⋅DB 3 3 1 1 1 1 1 1 1 1 1 28 3 1 ∴ = ⋅DD ⋅28 3，解得：DD =1 3 3 1 1 如图，以点D为原点，DA，DB，DD 所在直线为x轴，y轴，z轴， 1 建立如图的空间直角坐标系， 则A ( 4,0,0 )，B ( 0,4 3,0 ) ，C ( −4,4 3,0 ) ，B ( 0,2 3,1 ) 1   ( ) ∴BC =(−4,0,0 )，BB = 0,−2 3,1 1  设平面BCC B 的法向量为n=( x,y,z )， 1 1    n⋅BC =−4x=0  ( ) 则有  所以n= 0,1,2 3 n⋅BB =−2 3y+z =0 1  平面ADD A的法向量为m=( 0,1,0 )， 1 1 设平面ADD A与平面BCC B 所成锐二面角为θ 1 1 1 1     m⋅n 1 13 则cosθ= cos m,n =   = = ． m n 13 13 17．解：（1）由图估计甲班平均分较高 1 （2）由图可知，甲班中有 的学生分数低于128分； 2 学科网（北京）股份有限公司3 乙班中有 的学生分数低于128分 4 设从两班中随机抽取一人， “该同学来自甲班为事件A”，“该同学分数低于128分为事件B”， 则P ( A )= 1 ，P ( A ) = 1 ，P ( B A ) = 1 ，P ( B A ) = 3 ， 2 2 2 4 ∴P ( B )= P ( AB )+P ( AB ) = P ( B A ) ⋅P ( A )+P ( B A ) ⋅P ( A ) = 1 × 1 + 3 × 1 = 5 2 2 4 2 8 1 1 P ( AB ) P ( A ) P ( B A ) × 2 ( ) 2 2 P A B = = = = P ( B ) P ( B ) 5 5 8 P ( AB ) P ( A ) P ( B A ) 1 × 3 ( ) 2 4 3 P A B = = = = P ( B ) P ( B ) 5 5 8 2 3 所以，该同学来自甲乙两班的概率分别为 ， 5 5 （3）依题X 的所有可能取值为0，1，2，3 C3C0 1 C2C1 1 P ( X =0 )= 6 4 = ，P ( X =1 )= 6 4 = C3 6 C3 2 10 10 C1C2 3 C0C3 1 P ( X =2 )= 6 4 = ，P ( X =4 )= 6 4 = C3 10 C3 30 10 10 所以X 的分布列为： X 0 1 2 3 1 1 3 1 P 6 2 10 30 18．解：（1）设M ( x ,y )，N ( x ,y )，则x +x =2，y + y =6 1 1 2 2 1 2 1 2 M ，N 两点在双曲线C上 x2 y2  1 − 1 =1① a2 b2 x2 −x 2 y2 − y 2 ∴ ，由①－②得 1 2 − 1 2 =0 x 2 y 2 a2 b2 2 − 2 =1② a2 b2 y2 − y 2 b2 ( y + y )( y − y ) b2 即 1 2 = ，∴ 1 2 1 2 = x2 −x 2 a2 ( x +x )( x −x ) a2 1 2 1 2 1 2 b2 b2 ∴k ⋅k = ，即∴1⋅3= ，∴b2 =3a2 OQ MN a2 a2 学科网（北京）股份有限公司y2 又a =1，∴b2 =3，∴双曲线C的方程为：x2 − =1 3 （2）由已知可得，直线MN 的方程为：y−3=1⋅( x−1 )，即y = x+2 y = x+2 联立 ⇒2x2 −4x−7=0，∆=16+56=72>0 3x2 − y2 −3=0 7 则x +x =2，x x =− 1 2 1 2 2   EM ⋅EN =( x −1,y )⋅( x −1,y )=( x −1 )( x −1 )+ y y 1 1 2 2 1 2 1 2 =( x −1 )( x −1 )+( x +2 )( x +2 )=2x x +( x +x )+5 1 2 1 2 1 2 1 2  7 =2×  −  +2+5=0  2 ∴EM ⊥ EN，∴△EMN 为直角三角形 （3）由题意可知，若直线AB有斜率则斜率不为0， 故设直线AB方程为：x=my+n 设P ( x ,y )，A ( x ,y )，B ( x ,y ) 3 3 4 4 5 5   AP=λPB，∴( x −x ,y − y )=λ( x −x ,y − y ) 3 4 3 4 5 3 5 3   x +λx  x −x =λ( x −x )   x 3 = 4 1+λ 5 ∴ 3 4 5 3 ⇒ y − y =λ( y − y ) y +λy   3 4 5 3 y = 4 5   3 1+λ  x +λx  2  y +λy  2 4 5 4 5      1+λ   1+λ  点P在双曲线C上，∴ − =1 1 3 ∴3 ( x +λx )2 −( y +λy )2 =3 ( 1+λ)2 4 5 4 5 ∴ ( 3x2 − y2 ) +λ2 ( 3x2 − y2 ) +2λ( 3x x − y y )=3 ( 1+λ)2 ③ 4 4 5 5 4 5 4 5 又3x2 − y2 =0，3x2 − y2 =0， 4 4 5 5 3 ( 1+λ)2 ∴2λ( 3x x − y y )=3 ( 1+λ)2，∴3x x − y y = ④ 4 5 4 5 4 5 4 5 2λ 学科网（北京）股份有限公司3x2 − y2 =0 ( ) 联立 ⇒ 3m2 −1 y2 +6mny+3n2 =0 x=my+n  3m2 −1≠0 3  ⇒m≠± ( )  ∆=36m2n2 −12n2 3m2 −1 >0 3 −6mn 3n2 y + y = ⑤，y y = ⑥ 4 5 3m2 −1 4 5 3m2 −1 A，B分别在第一象限和第四象限，∴y y <0，∴3m2 −1<0 4 5 3 ( 1+λ)2 由④式得：3 ( my +n )( my +n )− y y = 4 5 4 5 2λ 3 ( 1+λ)2 ∴ ( 3m2 −1 ) y y +3mn ( y + y )+3n2 = ⑦ 4 5 4 5 2λ ( ) 3n2 −6mn 3 ( 1+λ)2 将⑤⑥代入⑦得：∴ 3m2 −1 +3mn +3n2 = 3m2 −1 3m2 −1 2λ −6n2 3 ( 1+λ)2 ∴ = 3m2 −1 2λ 1 3 2 3 2 3 ∴S = OA ⋅ OB ⋅sin∠AOB= ⋅ ⋅ y ⋅ ⋅ y △AOB 2 4 3 1 3 2 3 3 3n2 n2 = y y = =− 3⋅ 3 1 2 3 3m2 −1 3m2 −1 1 3 ( 1+λ)2 3  1  = ⋅ =  λ+ +2 2 3 2λ 4 3 λ  1 1  令h (λ)=λ+ ，λ∈ ,2   λ 3  1 (λ+1 )(λ−1 ) 1  h′(λ)=1− = ，λ∈ ,2   λ2 λ2 3  1  ∴λ∈  ,1 ，h′(λ)<0，h (λ)单调递减 3  λ∈( 1,2 ]，h′(λ)>0，h (λ)单调递增 学科网（北京）股份有限公司 10  4 3 ∴h (λ)∈   2, 3   ，∴S △AOB ∈  3, 3   19．（1）证明：8n+3=a ⋅2k+3 +a ⋅2k+2 +⋅⋅⋅+a ⋅23 +1⋅21+1 0 1 k ∴S ( 8n+3 )=a +a +⋅⋅⋅+a +1+1=S ( n )+2 0 1 k 4n+3=a ⋅2k+2 +a ⋅2k+1+⋅⋅⋅+a ⋅22 +1⋅21+1 0 1 k ∴S ( 4n+3 )=a +a +⋅⋅⋅+a +1+1=S ( n )+2 0 1 k ∴S ( 8n+3 )=S ( 4n+3 ) （2）（ⅰ）解：60=32+16+8+4=( 111100 ) ，∴I ( 60 )=2 2 （ⅱ）解：1=( 1 ) ，511=( 111111111 ) ，故从n=1到n=511中 2 2 I ( n )=0有9个， I ( n )=1有C1+C1+⋅⋅⋅C1 =C2个， 1 2 8 9 I ( n )=2有C2 +C2 +⋅⋅⋅C2 =C3个， 2 3 8 9 ……， I ( n )=9有C8 =C9 =1个， 8 9 511 ∑2I(n) =9×20 +C2×21+C3×22 +⋅⋅⋅C9×28 9 9 9 n=1 C1×21+C2×22 +C3×23 +⋅⋅⋅C9×29 = 9 9 9 9 2 C0×20 +C1×21+C2×22 +C3×23+⋅⋅⋅C9×29 −1 = 9 9 9 9 9 2 ( 1+2 )9 −1 = =9841 2 学科网（北京）股份有限公司