文档内容
5.2 导数的运算
【题组一 初等函数求导】
1.(2018·全国高二课时练习)求函数 在下列各点处的导数.
(1) ; (2) ; (3) .
【答案】(1) (2)-1 (3)
【解析】∵ ,∴ .
(1)当 时, .
(2)当 时, .
(3)当 时, .
2.求下列函数的导数:
(1) ;
(2) ;
(3) .
【答案】(1) ;(2) ;(3)
【解析】(1)y′=( )′=(2)∵y=cos =sin x,∴y′=(sin x)′=cos x.
(3)y′=[( )x]′=( )xln = .
3.(2020·海林市朝鲜族中学高二课时练习)求下列函数的导数:
(1) ;
(2) .
【答案】(1) ;(2)
【解析】(1)y′= ′= ′cos x+ (cos x)′= ′cos x- sin x=- x- cos x-
sin x=- - sin x=- .
(2)∵y=x =x3+1+ ,∴y′=3x2- .
4.(2020·海林市朝鲜族中学高二课时练习)求下列函数的导数.
(1) ;
(2)f(x)=(5x-4)cos x;
(3) .
【答案】(1) ;(2) ;(3)
【解析】(1)∵ ,∴ .
(2)∵f(x)=(5x-4)cos x,∴ .
(3)∵ ,∴ .
【题组二 复合函数求导】
1.(2020·宁县第二中学高二期中(理))求下列函数的导数:
(1)
(2)
【答案】(1) ;(2)
【解析】(1) , .
(2) ,
2.(2020·江苏徐州·高二月考)求下列函数的导数.
(1)
(2)
(3)
【答案】(1) ;(2) ;(3)
【解析】(1) ;
(2);
(3) .
3.(2020·江苏省如东高级中学高二期中)求下列函数的导函数.
(1)
(2)
【答案】(1) ;(2)
【解析】(1) ;
(2) , .
4.(2020·陕西泾阳·高二期中(理))求下列函数的导数:
(Ⅰ) ;
(Ⅱ) .
【答案】(Ⅰ) (Ⅱ)
【解析】(Ⅰ) .
(Ⅱ) .
5.(2020·长春兴华高中高二期末(文))求下列函数的导数:(1) ;
(2)y= ;
(3) ;
【答案】(1)y′=exsinx+excosx.(2)y′=3x2- .(3)y′=1- cosx.
【解析】(1)y′=(ex)′sinx+ex(sinx)′=exsinx+excosx..
(2)因为y=x3+ +1,所以y′=3x2- .
(3)因为y=x- sinx,所以y′=1- cosx.
6.(2020·江西南昌·高二期末(理))求出下列函数的导数.
(1)
(2)
(3)
(4)
(5)
【答案】(1) ;(2) ;(3) ;
(4) ;(5)【解析】(1)由 ,
则 ,
即
(2)由 ,则
(3)由 ,则 ,
(4)由 ,则 ,
(5)由 ,则 .
【题组三 求导数值】
1.(2020·四川高二期中(理))已知 ,则 ( )
A. B. C. D.
【答案】C
【解析】由 .故选:C.
2.(2020·江西高二期末(理))若函数 的导数 满足 ,则 (
)
A.e B.2 C.1 D.0
【答案】D
【解析】∵ ,∴ ,令 ,可得 ,解得 ,
因此 , ,故选:D
3.(2020·四川省南充市白塔中学高二开学考试(文))已知函数 的导函数为 ,且满足关系
式 ,则 的值等于( )
A. B. C. D.
【答案】D
【解析】依题意 ,令 得 , ,故
选D.
4.(2020·四川棠湖中学高二月考(文))若函数f(x)满足f(x)= x3-f′(1)·x2-x,则f′(1)的值为( )
A.1 B.2 C.0 D.-1
【答案】C
【解析】依题意 ,令 得 ,解得 ,故选C.
5.(2020·河南商丘·高二期末(理))已知函数 ,则 ( )
A.2 B.1 C.0 D.
【答案】D
【解析】因为 ,则 ,
所以 ,则 ,
所以 ,所以 .故选:D.6.(2020·江西高二期末(文))已知函数 的导函数为 ,且满足 ,则
______.
【答案】
【解析】因为 ,所以 ,
将 代入得 ,解得 ,故答案为: .
7.(2020·四川内江·高二期末(文))已知 ,则 ________.
【答案】
【解析】因为 ,所以 所以
所以 .故答案为: .
【题组四 求切线方程】
1.(2020·湖南高二期末)曲线 在点 处的切线方程为 ______.
【答案】
【解析】因为 ,所以切线斜率 ,
所以曲线 在点 处的切线方程为: .
故答案为:
2.(2020·江西高二期末(理))已知函数 为偶函数,则 在其图象上的点
处的切线的斜率为______.【答案】
【解析】 函数 为偶函数,
,即 ,解得 ,则 ,
在点 处的切线的斜率 .故答案为: .
3.(2020·陕西西安·高新一中高三期末(文))曲线 在点 处的切线方程为________.
【答案】
【解析】 ,所以切线方程为 .故答案为: .
4.(2020·重庆八中高三月考)已知函数 为奇函数,当 时, ,则曲线
在点 处的切线方程为________.
【答案】
【解析】∵函数 是奇函数, ,
当 时, ,不妨设 ,则 ,
故 ,故 时, ,
故 ,故 , ,
故切线方程是: ,整理得: ,故答案为: .
5.(2020·重庆高三期中(文))曲线 在点 处的切线与坐标轴围成的三角形的
面积为____________.【答案】
【解析】 , ,
, ,
切线方程为: 即 ,
当 ,时 ,当 ,时 ,
三角形面积为: .
故答案为: .
6.(2020·五华·云南师大附中高三月考(理))曲线 在 处的切线方程为______.
【答案】
【解析】 ,当 时,切线斜率 ,
故切线方程为 ,即 .
故答案为:
7.(2020·江西高三月考(理)) 的图像在 处的切线方程为________.
【答案】
【解析】 ,则 ,且
切线方程为 ,即故答案为:
8.(2020·五华·云南师大附中高三月考(文))过原点与曲线 相切的切线方程为______.
【答案】
【解析】设切点坐标为 ,切线方程为 ,
由 ,则 ,则 ,
则 ,即 ,即 ,解得 ,所以 ,
所以原点与曲线 相切的切线方程为 .
故答案为:
9.(2020·黑龙江萨尔图·大庆实验中学高二期末(文))已知 ,则曲线 过点
的切线方程是______.
【答案】 或
【解析】设切点为 ,
的导数为 ,可得切线的斜率为 ,
又 ,解得 或 ,
当 时, ; 时, ;
曲线 过点 的切线方程为 ,则切线的方程为 或 .
故答案为: 或 .
10.(2020·黑龙江道里·哈尔滨三中(文))过函数 上的点 的切线方程是
_________.
【答案】 或
【解析】因为
设切点为 ,则 ,
所以切线方程为: ,
因为 在切线方程上,
所以 ,解得: 或 .
当 时, ,此时切线方程为 ;
当 时, ,此时切线方程为 .
所以,切线方程为: 或 .
故答案为: 或 .
11.(2020·辽宁省本溪满族自治县高级中学高三其他(文))过点 作曲线 ( )
的切线,则切点坐标为________.
【答案】
【解析】由 ( ),则 ,化简得 ,
则 ,设切点为 ,显然 不在曲线上,则 ,得 ,则切点坐标为 .
故答案为: .
12.(2020·石嘴山市第三中学高二期末(理))过点 与曲线 相切的直线方程为
______________.
【答案】 .
【解析】设切点坐标为 ,
由 得 ,
切线方程为 ,
切线过点 ,
,即 ,
,
即所求切线方程为 .
故答案为: .
13.(2020·吉林净月高新技术产业开发区·东北师大附中高二月考(理))过点 作曲线 的切线,
则切线方程是______.
【答案】 和
【解析】设切点坐标为 ,对函数 求导得 ,则所求切线的斜率为 ,
所以,曲线 在点 处的切线方程为 ,由于该直线过点 ,即 ,整理得 ,解得 或 .
当 时,所求切线的方程为 ,即 ;
当 时,所求切线的方程为 ,即 .
故答案为: 和 .
【题组五 利用切线求参数】
1.(2020·辽宁高二期末)已知函数 ,若 ,则实数 的值为
( )
A.2 B.1 C. D.
【答案】A
【解析】根据题意,函数 ,
其导数 ,则 ,
又由 ,即 ,解可得 ;
故选:A.
2.(2020·湖北省天门中学高二月考)曲线 在 处的切线平行于直线 ,则
点的坐标为( )
A.(1, 0) B.(2, 8)
C.(1, 0)和(-1, -4) D.(2, 8)和(-1, -4)
【答案】C
【解析】依题意,令 ,解得故 点的坐标为(1, 0)和(-1, -4),
故选:C
3.(2020·甘肃城关·兰州一中高二期中(文)) 设函数f(x)= -aln x,若f′(2)=3,则实数a的值
为( )
A.4 B.-4
C.2 D.-2
【答案】B
【解析】f′(x)= - ,故f′(2)= - =3,因此a=-4.
4.(2020·唐山市第十一中学高二期末)设 ,若 ,则 =( )
A. B. C. D.
【答案】C
【解析】对 求导得
将 带入有 .
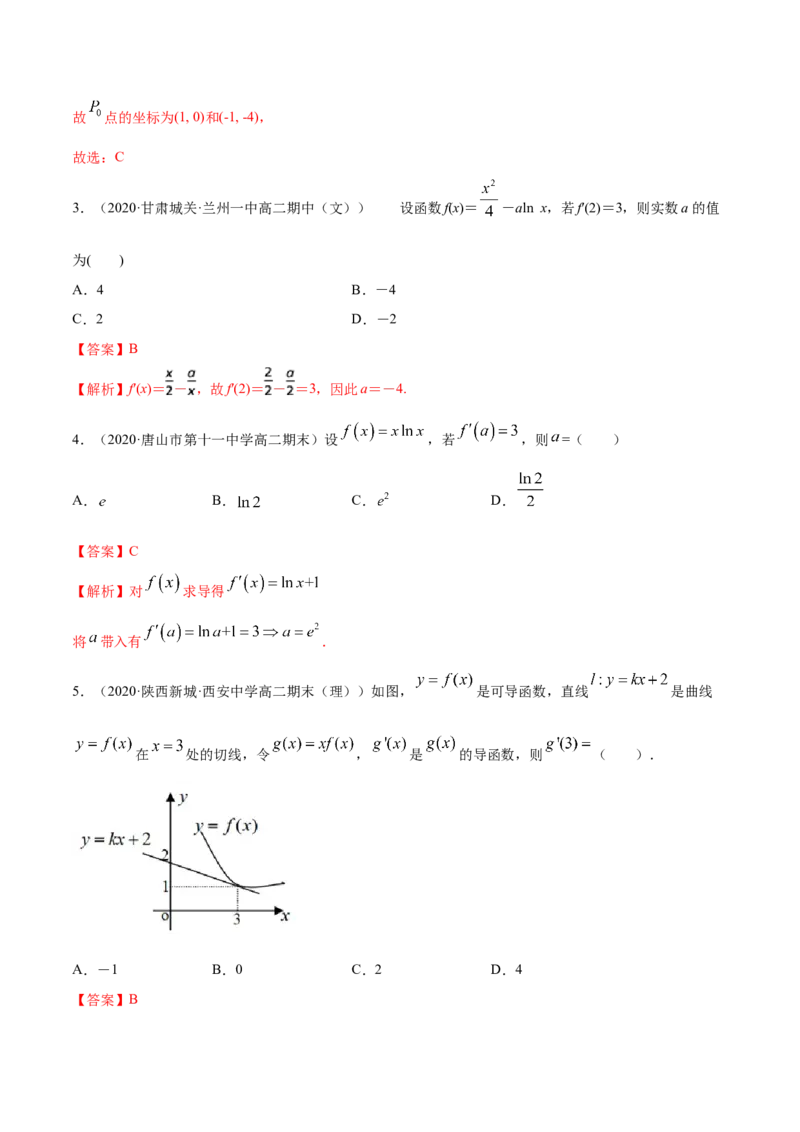
5.(2020·陕西新城·西安中学高二期末(理))如图, 是可导函数,直线 是曲线
在 处的切线,令 , 是 的导函数,则 ( ).
A.-1 B.0 C.2 D.4
【答案】B【解析】将点 代入直线 的方程得 ,得 ,所以, ,
由于点 在函数 的图象上,则 ,
对函数 求导得 ,
,故选B.