文档内容
5.3.1函数的单调性(1) -B提高练
一、选择题
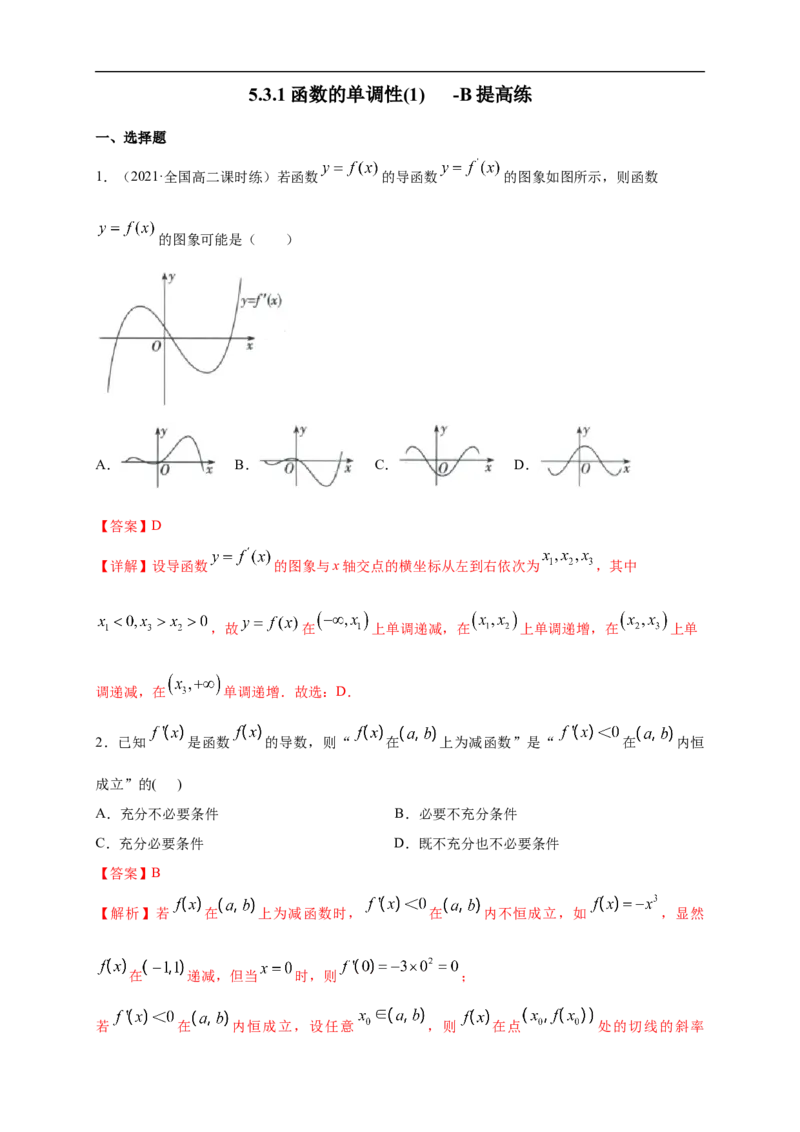
1.(2021·全国高二课时练)若函数 的导函数 的图象如图所示,则函数
的图象可能是( )
A. B. C. D.
【答案】D
【详解】设导函数 的图象与x轴交点的横坐标从左到右依次为 ,其中
,故 在 上单调递减,在 上单调递增,在 上单
调递减,在 单调递增.故选:D.
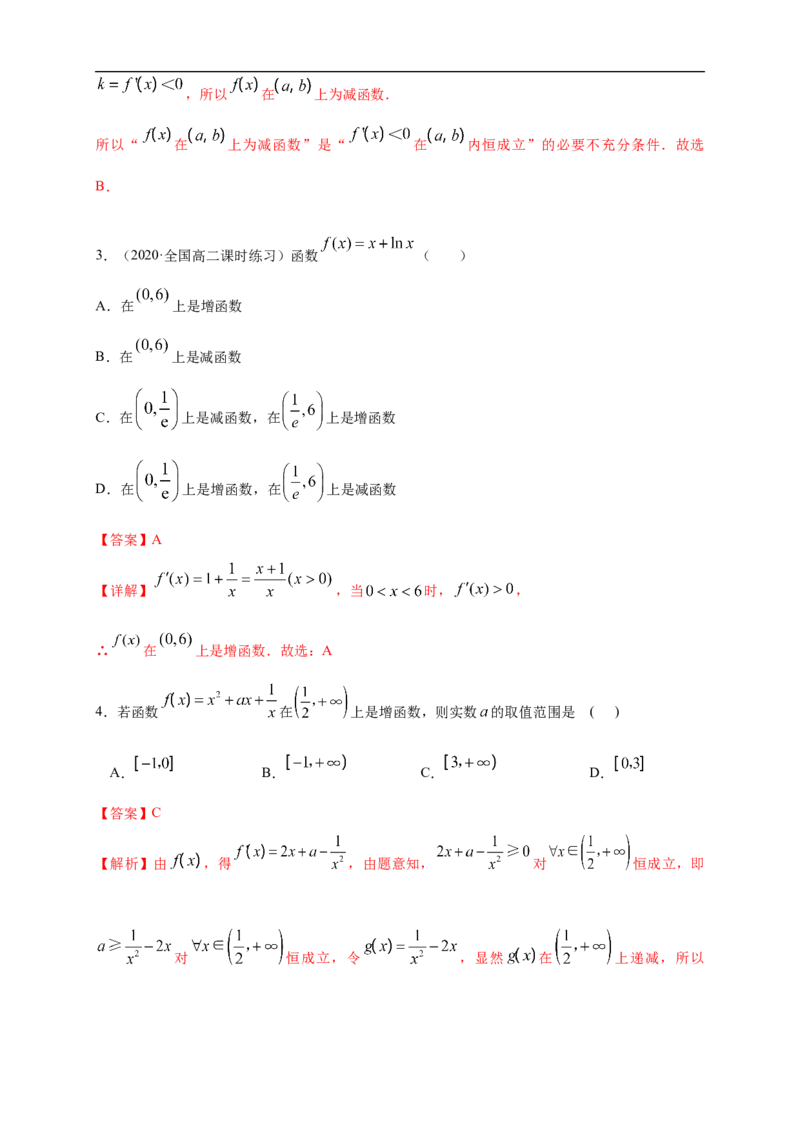
2.已知 是函数 的导数,则“ 在 上为减函数”是“ 在 内恒
成立”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】B
【解析】若 在 上为减函数时, 在 内不恒成立,如 ,显然
在 递减,但当 时,则 ;
若 在 内恒成立,设任意 ,则 在点 处的切线的斜率,所以 在 上为减函数.
所以“ 在 上为减函数”是“ 在 内恒成立”的必要不充分条件.故选
B.
3.(2020·全国高二课时练习)函数 ( )
A.在 上是增函数
B.在 上是减函数
C.在 上是减函数,在 上是增函数
D.在 上是增函数,在 上是减函数
【答案】A
【详解】 ,当 时, ,
∴ 在 上是增函数.故选:A
4.若函数 在 上是增函数,则实数 的取值范围是 ( )
A. B. C. D.
【答案】C
【解析】由 ,得 ,由题意知, 对 恒成立,即
对 恒成立,令 ,显然 在 上递减,所以,所以 .故选C.
5.(多选题)(2020·广东揭阳市高二期中)下列函数在其定义域上既是奇函数又是减函数的是(
)
A. B. C. D.
【答案】BCD
【详解】对于A, 既不是奇函数也不是偶函数,且单调递增,故A错误;
对于B, 的定义域为 ,且 , 是奇函
数,又 恒成立,故 是减函数,故B正确;
对于C, 的定义域为 ,且 , 是奇函数,
,故 是减函数,故C正确;
对于D, 的定义域为 ,且 , 是奇函数,又
是减函数,故D正确.故选:BCD.
6.(多选题)(2020·湖南师大附中高二月考)素数分布问题是研究素数性质的重要课题,德国数
学家高斯提出了一个猜想: ,其中 表示不大于x的素数的个数,即随着x的增大,
的值近似接近 的值.从猜想出发,下列推断正确的是( )
A.当x很大时,随着x的增大, 的增长速度变慢
B.当x很大时,随着x的增大, 减小C.当x很大时,在区间 (n是一个较大常数)内,素数的个数随x的增大而减少
D.因为 ,所以
【答案】AC
【详解】设函数 且 ,则 且 ,
且 ,当 时, ,
所以当x很大时,随着x的增大, 的增长速度变慢,故A正确;
函数 的图象如图所示:
由图象可得随着x的增大, 并不减小,故B错误;当x很大时,在区间 (n是一个
较大常数)内,函数增长得慢,素数的个数随x的增大而减少,故C正确; ,故D
错误.故选:AC.
二、填空题
7.(2021·山东菏泽三中高二期末)函数 的单调减区间是______ .
【答案】
【解析】函数的定义域为 , ,令 ,得 函数的单调递减区间是 ,故答案为 .
8.(2021·全国高二课时练)函数y=xsin x+cos x,x∈(-π,π)的单调增区间是__________.
【答案】
【解析】 ,当 时, , ;
当 时, ;
当 时, ;
当 时, ,
故函数的单调增区间是 和 .
9.(2021·全国高课二时练)若函数 在 上为减函数,则实数 的取值范围是
__________.
【答案】(-∞,-1]
【解析】因为 是R上的减函数,所以 恒成立,即 ,
即 恒成立,因为 ,所以 ,故答案为 .
10.(2021·全国高二课时练)若函数f(x)=ax3+x恰有3个单调区间,则a的取值范围为________.
【答案】(-∞,0)
【解析】由f(x)=ax3+x,得f′(x)=3ax2+1.
若a≥0,则f′(x)>0恒成立,此时f(x)在(-∞,+∞)上为增函数,不满足题意;
若a<0,由f′(x)>0得- ,
即故当a<0时,f(x)的单调递增区间为(- , ),单调递减区间为(-∞,- ), (,+∞),满足题意.答案为:(-∞,0).
三、解答题
11.已知函数 .
(1)若函数 在 上单调递增,求实数 的取值范围;
(2)若函数 的单调递减区间是 ,求实数 的值;
(3)若函数 在区间 上单调递减,求实数 的取值范围.
【解析】由 ,得 .
(1)因为 在 上单调递增,所以 对 恒成立,即 对 恒成立,
只需 ,而 ,所以 ,经检验,当 时,符合题意,故 的取值范
围是 .
(2)令 ,因为 的单调递减区间是 ,则不等式 的解集为 ,所
以 和 是方程 的两个实根,所以 ,得 .
(3)因为函数 在区间 上单调递减,所以 对 恒成立,即
对 恒成立,易得函数 的值域为 ,所以 ,即实数 的取值
范围是 .
12.(2021·甘肃武威市十八中高二课时练)已知a是实数,函数 .
(1)若 ,求a的值及曲线 在点 处的切线方程;
(2)讨论函数 在区间 上的单调性.【详解】(1) , ,
则 , , , ,
因此,曲线 在点 处的切线方程为 ,即 ;
(2) , ,
令 ,得 , .
①当 时,即当 时,对任意的 , ,
此时,函数 在区间 上单调递增.
②当 时,即当 时,
此时,当 ,则 ;
当 时, .
此时,函数 在区间 上单调递减,在区间 上单调递增;
③当 时,即当 时,对任意的 , .
此时,函数 在区间 上单调递减.
综上所述,当 时,函数 在区间 上单调递增;
当 时,函数 在区间 上单调递减,在区间 上单调递增;
当 时,函数 在区间 单调递减.