文档内容
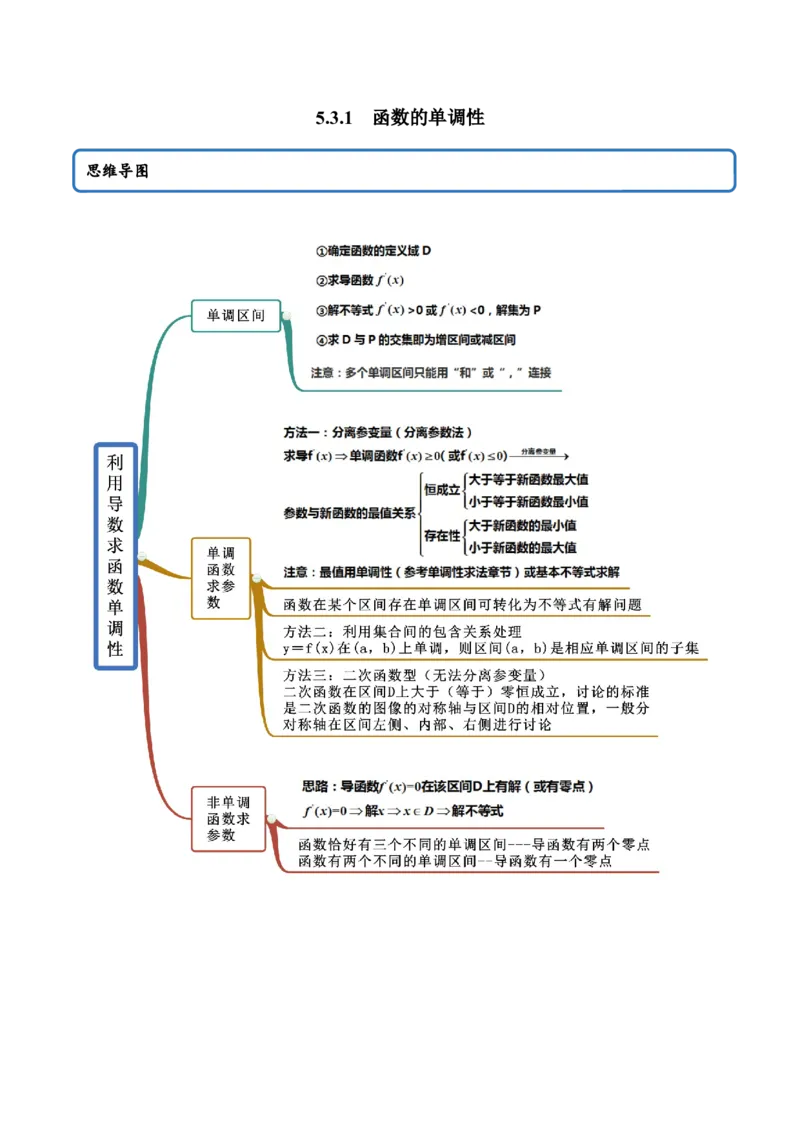
5.3.1 函数的单调性
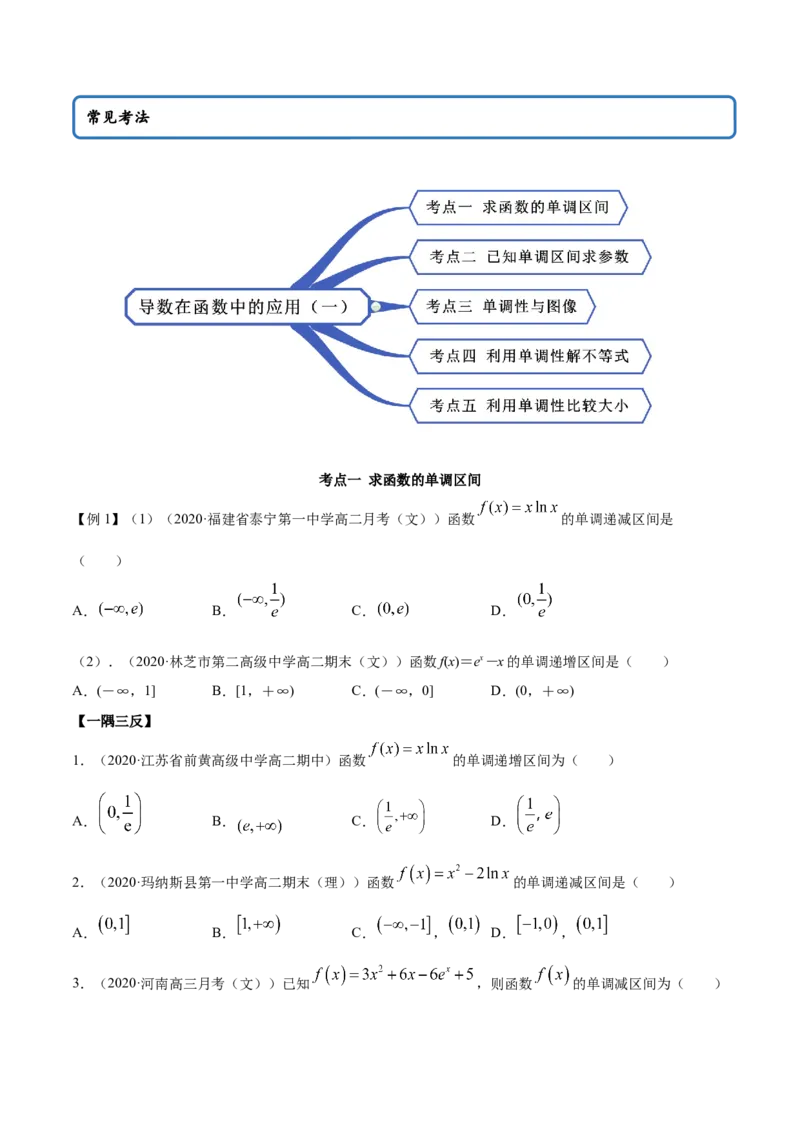
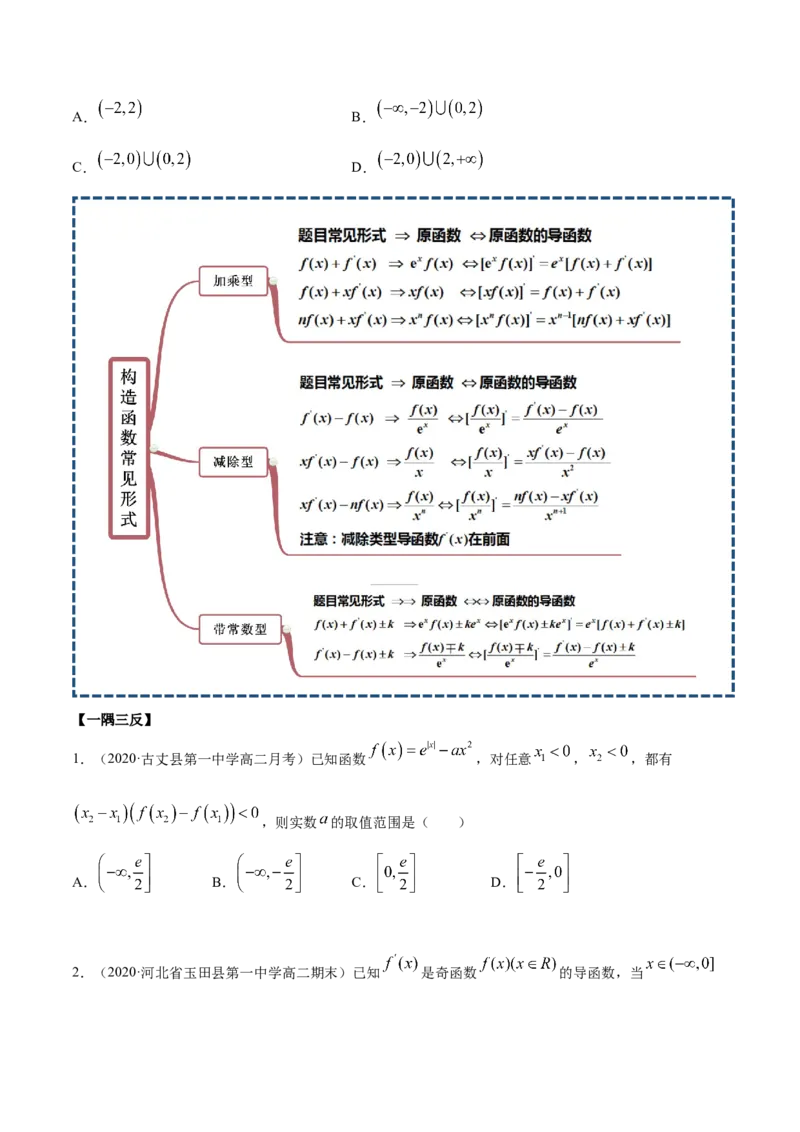
思维导图常见考法
考点一 求函数的单调区间
【例1】(1)(2020·福建省泰宁第一中学高二月考(文))函数 的单调递减区间是
( )
A. B. C. D.
(2).(2020·林芝市第二高级中学高二期末(文))函数f(x)=ex-x的单调递增区间是( )
A.(-∞,1] B.[1,+∞) C.(-∞,0] D.(0,+∞)
【一隅三反】
1.(2020·江苏省前黄高级中学高二期中)函数 的单调递增区间为( )
A. B. C. D.
2.(2020·玛纳斯县第一中学高二期末(理))函数 的单调递减区间是( )
A. B. C. , D. ,
3.(2020·河南高三月考(文))已知 ,则函数 的单调减区间为( )A. B. C. D.
考点二 已知单调性求参数
【例2】(1)(2020·北京高二期末)已知函数 在区间 上单调递增,则a的取值
范围是( )
A. B. C. D.
(2).(2020·山东德州·高二期末)若函数 在(0,1)上不单调,则 的取值范围
是( )
A. B.
C. D.
【一隅三反】
1.(2020·广东汕尾·高二期末)已知函数 在 上单调递增,则实数a的取值范
围是( )
A. B. C. D.
2.(2020·广东禅城·佛山一中高二月考)已知函数 在区间 上是增函数,
则实数m的取值范围为( )
A. B. C. D.
3.(2020·甘肃城关·兰州一中高二期中(理))若函数 在区间 内存在单调递
增区间,则实数 的取值范围是( )A. B. C. D.
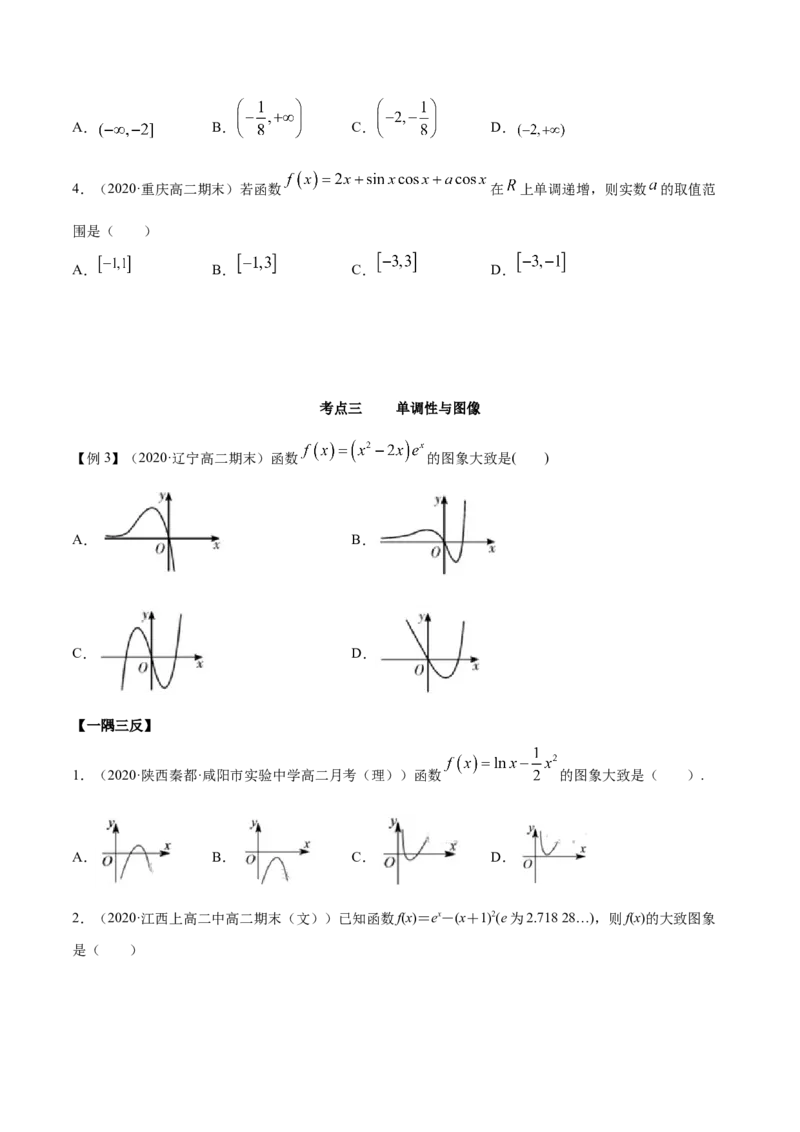
4.(2020·重庆高二期末)若函数 在 上单调递增,则实数 的取值范
围是( )
A. B. C. D.
考点三 单调性与图像
【例3】(2020·辽宁高二期末)函数 的图象大致是( )
A. B.
C. D.
【一隅三反】
1.(2020·陕西秦都·咸阳市实验中学高二月考(理))函数 的图象大致是( ).
A. B. C. D.
2.(2020·江西上高二中高二期末(文))已知函数f(x)=ex-(x+1)2(e为2.718 28…),则f(x)的大致图象
是( )A. B.
C. D.
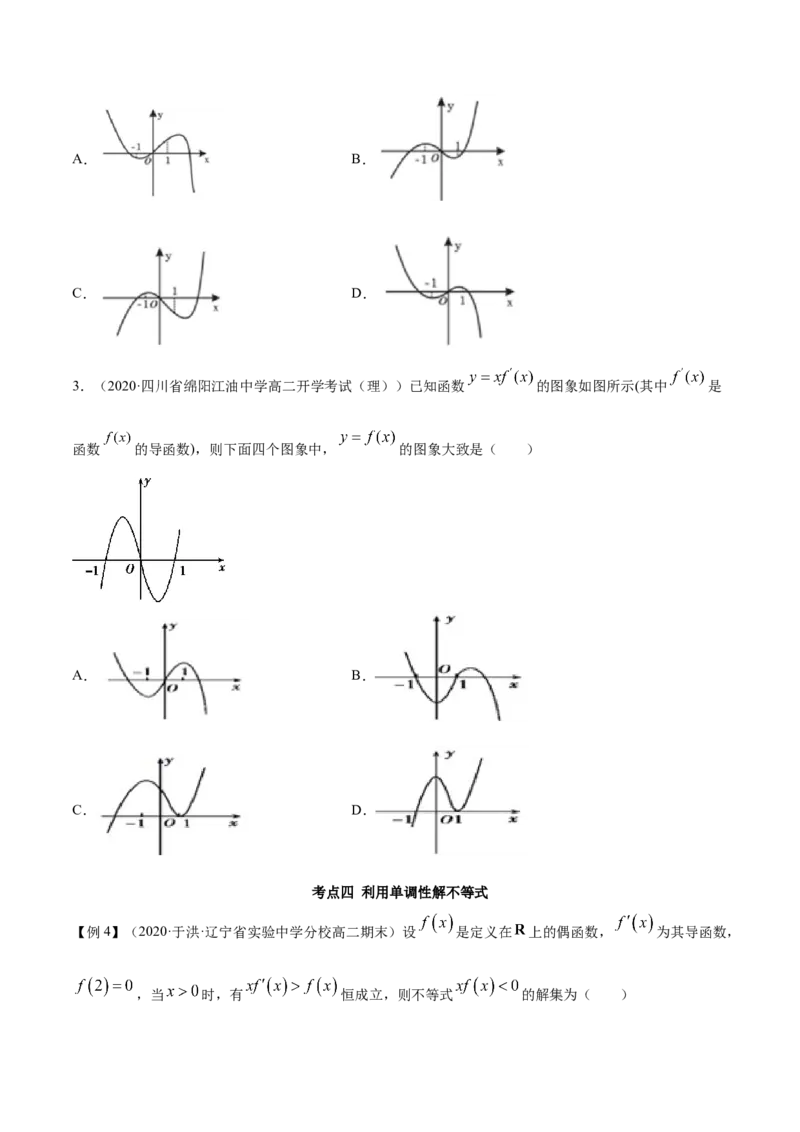
3.(2020·四川省绵阳江油中学高二开学考试(理))已知函数 的图象如图所示(其中 是
函数 的导函数),则下面四个图象中, 的图象大致是( )
A. B.
C. D.
考点四 利用单调性解不等式
【例4】(2020·于洪·辽宁省实验中学分校高二期末)设 是定义在 上的偶函数, 为其导函数,
,当 时,有 恒成立,则不等式 的解集为( )A. B.
C. D.
【一隅三反】
1.(2020·古丈县第一中学高二月考)已知函数 ,对任意 , ,都有
,则实数 的取值范围是( )
A. B. C. D.
2.(2020·河北省玉田县第一中学高二期末)已知 是奇函数 的导函数,当时, ,则不等式 的解集为
A. B. C. D.
3.(2020·青海高二期末(理))已知函数 满足 ,则实
数 的取值范围是( )
A. B. C. D.
考点五 利用单调性比较大小
【例5】.(2020·四川阆中中学高三开学考试(理))已知 ,则( )
A. B.
C. D.
【一隅三反】
1.(2020·黑龙江工农·鹤岗一中高二期末(理))对任意 ,不等式
恒成立,则下列不等式错误的是( )
A. B.
C. D.
2.(2020·陕西莲湖·西安一中高三月考(理))若 则( )
A. B.C. D.