文档内容
专题 02 二项式定理
一、单选题
1.(2020·吐鲁番市高昌区第二中学高二期末) 展开式中的常数项为( )
A.第5项 B.第5项或第6项 C.第6项 D.不存在
【答案】C
【详解】
解:根据题意, 展开式中的通项为 ,
令 ,可得 ;则其常数项为第 项;
故选 .
2.(2021·全国高二课时练习)在 的展开式中, 项的系数为( )
A. B. C.30 D.50
【答案】B
【详解】
表示5个因式 的乘积,在这5个因式中,
有2个因式都选 ,其余的3个因式都选1,相乘可得含 的项;
或者有3个因式选 ,有1个因式选 ,1个因式选1,相乘可得含 的项,
故 项的系数为 ,
故选B.
3.(2020·江苏高一期中)二项式 的展开式中含有非零常数项,则正整数 的最小值为()
A. B. C. D.
【答案】B
【详解】
由 得:
展开式的通项为 ,
令 ,
据题意此方程有解,
,
当 时,
最小为 ,
故选:B.
4.(2021·山东济宁市·高三一模)若 的展开式中 的系数是80,则实数
( )
A. B. C.1 D.2
【答案】A
【详解】
二项式展开式的通项为 ,
令 ,得 ,
则 ,所以 ,解得 .
故选:A5.(2020·山东枣庄市·高二期末)若 展开式的常数项等于 ,则 ( )
A. B. C.2 D.3
【答案】C
【详解】
解: 展开式的通项公式为: ,
所以当 时, 项的系数为: ,
的展开式无常数项,
所以 展开式的常数项为: ,解得:
故选:C.
6.(2021·贵州高三开学考试(理))已知二项式 的展开式中,第二项和第四项的二项式系数相
等,则 ( )
A.6 B.5 C.4 D.3
【答案】C
【详解】
因为二项式展开式中第二项和第四项的二项式系数相等,
所以 ,
所以 ,
故选:C
7.(2021·湖北黄冈市·高二期末)已知二项式 的展开式中仅有第4项的二项式系数最大,则展开式中 项的系数为( )
A.-80 B.80 C.-160 D.-120
【答案】C
【详解】
解:因为二项式 的展开式中仅有第4项的二项式系数最大,所以 ,所以 的展开式的
通项为 ,令 ,得 ,故 ,故展开式中
的系数为
故选:C
8.(2020·安徽省太和第一中学高二月考(理))已知
,则 ( )
A. B.0 C.14 D.
【答案】B
【详解】
解:由题知, ,
且 ,
则 ,
,
所以 .
故选:B.
9.(多选)(2021·全国高三其他模拟)已知 ,则( )
A.B.
C.
D.
【答案】ABC
【详解】
因为
令 ,得 ,故选项A正确;
令 ,得 ,
所以 ,故选项C正确;
易知该二项展开式的通项 ,所以 ,故选项B正确;
对 两边同时求导,得 ,
令 ,得 ,故选项D错误.
故选::ABC
10.(多选)(2021·全国高二课时练习)(多选题)若二项式 展开式中的常数项为15,则实数m
的值可能为( )
A.1 B.-1
C.2 D.-2
【答案】AB
【详解】
二项式 展开式的通项为,,
令 ,得 ,
常数项为 ,
,得 ,故答案为 .
故选:AB
11.(多选)(2020·江苏宿迁市·宿迁中学高二期中)对于 展开式的二项式系数下列结论
正确的是( )
A. B.
C.当 为偶数时, D.
【答案】ABCD
【详解】
解:选项A:由组合数的运算直接可得 ,故选项A正确;
选项B:由杨辉三角直接可得 ,故选项B正确;
选项C:二项式展开式中,令 ,不论 为奇数还是偶数,都可得 ,故
选项C正确;
选项D:由选项C可知 ,故选项D正确.
故选:ABCD
12.(多选)(2021·江苏省天一中学高三二模)已知 的展开式中各项系数的和为2,则
下列结论正确的有( )
A.
B.展开式中常数项为160C.展开式系数的绝对值的和1458
D.若 为偶数,则展开式中 和 的系数相等
【答案】ACD
【详解】
对于A,
令二项式中的 为1得到展开式的各项系数和为 ,
,故A正确;
对于B,
,
展开式的通项为 ,
当 展开式是中常数项为:令 ,得
可得展开式中常数项为: ,
当 展开式是中常数项为:
令 ,得 (舍去)
故 的展开式中常数项为 .故B错误;对于C,求其展开式系数的绝对值的和与 展开式系数的绝对值的和相等
,令 ,可得:
展开式系数的绝对值的和为: .故C正确;
对于D,
展开式的通项为 ,
当 为偶数,保证展开式中 和 的系数相等
① 和 的系数相等,
展开式系数中 系数为:
展开式系数中 系数为:
此时 和 的系数相等,
② 和 的系数相等,
展开式系数中 系数为:
展开式系数中 系数为:
此时 和 的系数相等,③ 和 的系数相等,
展开式系数中 系数为:
展开式系数中 系数为:
此时 和 的系数相等,
故D正确;
综上所在,正确的是:ACD
故选:ACD.
二、填空题
13.(2020·全国高二课时练习)在如图所示的三角形数阵中,从第3行开始,每一行除1以外,其他每一
个数字都是其上一行的左、右两个数字之和.若在此数阵中存在某一行,满足该行中有三个相邻的数字之比
为 ,则这一行是第______行(填行数).
第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
【答案】98
【详解】
三角形数阵中,第n行的数由二项式系数 组成,
如果第n行中有 , ,
那么 ,解得 ,
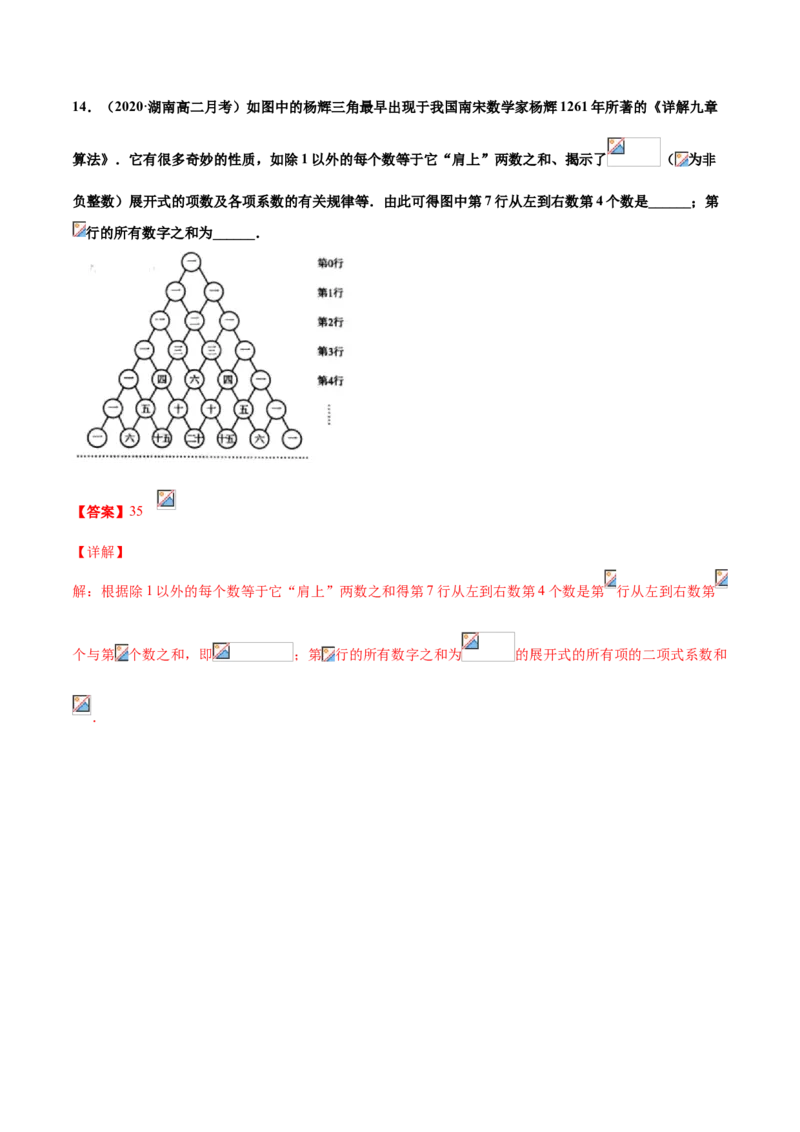
故答案为:98.14.(2020·湖南高二月考)如图中的杨辉三角最早出现于我国南宋数学家杨辉1261年所著的《详解九章
算法》.它有很多奇妙的性质,如除1以外的每个数等于它“肩上”两数之和、揭示了 ( 为非
负整数)展开式的项数及各项系数的有关规律等.由此可得图中第7行从左到右数第4个数是______;第
行的所有数字之和为______.
【答案】35
【详解】
解:根据除1以外的每个数等于它“肩上”两数之和得第7行从左到右数第4个数是第 行从左到右数第
个与第 个数之和,即 ;第 行的所有数字之和为 的展开式的所有项的二项式系数和
.