文档内容
专题 2.2 基本不等式
知识点 ① 基本不等式
1.基本不等式:≤
2.基本不等式成立的条件:a>0,b>0.
3.等号成立的条件:当且仅当a=b时,等号成立.
4.其中叫做正数a,b的算术平均数,叫做正数a,b的几何平均数.
知识点 ② 几个重要的不等式
1.a2+b2≥2ab(a,b∈R).
2.+≥2(a,b同号).
(a+b) 2
2
3.ab≤ (a,b∈R).
(a+b) 2
2
4.≥ (a,b∈R).
以上不等式等号成立的条件均为a=b.
知识点 ③ 利用基本不等式求最值
1.已知x,y都是正数,如果积xy等于定值P,那么当x=y时,和x+y有最小值2.
2.已知x,y都是正数,如果和x+y等于定值S,那么当x=y时,积xy有最大值S2.
注意:利用不等式求最值应满足三个条件“一正、二定、三相等”.
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大
值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则
这个定值就不是所求的最值,这也是最容易发生错误的地方.
题型一
解法突破:两种常数处理方法 .
例1 求 的最小值( ).
解: 因为 所以令 解得 (舍)
例2 求 的最小值( ).
解: 因为 所以
令 解得
(舍)
1.以分式分母为主进行配凑使其定积
2.注意变量范围,是否满足一正和三相等
题型二
解法突破: “1”的代换
例1已知 , 求 的最小值
解:
例2 已知 求 的最小值
解 : ,
【审题要津和评注】此类题型主要核心是“1”的等价代换,以及以分式分母为依据构造倒数形式,注意例
5,例6两个题目
题型三 消元法
解法突破:此类题目特点是有多个变量,且变量间满足等式关系
例1已知 求 的最小
解: ,
题型四 换元法:一般求谁最值换谁为t
例1已知 求 的最小
解 :
令 则 或 (舍)即 的最小是6
【审题要津和评注】
1.题型二的例三和题型三题型四比较类似注意区分
2.若一个题目在连用多个基本不等式时需注意取等时自变量取值是否相同
题型五 基本不等式的使用条件
解法突破:使用基本不等式前要注意验证使用条件是否满足
例1已知 求 的最大值,
解:
一、单选题
1.下列说法正确的为( )
A.
B.函数 的最小值为4
C.若 则 最大值为1
D.已知 时, ,当且仅当 即 时, 取得
最小值8
2.函数 有( )
A.最大值 B.最小值 C.最大值2 D.最小值2
3.已知 ,则 的最小值是( )
A.5 B.4 C.8 D.6
4.已知 ,且 ,则 的最小值是( )
A.6 B.8 C.14 D.165.设 , ,且 ,则 的最大值为( ).
A. B. C. D.
6.下列不等式恒成立的是( )
A. B.
C. D.
7.已知正实数a、b满足 ,则 的最小值为( )
A. B.4 C. D.
8.已知 x,y>0,当x+y=2时,求 的最小值( )
A. B. C. D.
9.已知 为正实数,且 ,则 的最小值为( )
A. B. C. D.
10.已知x,y都是正数,若 ,则 的最小值为( )
A. B. C. D.1
11.已知 , ,且 ,则 的最小值为( )
A.8 B. C.9 D.
12.已知正实数a、b满足 ,若 的最小值为4,则实数m的取
值范围是( )
A. B. C. D.
13.若 ,且 ,则下列不等式中成立的是( )A. B.
C. D.
14.已知实数 ,则 的最小值是( )
A.1 B. C.2 D.
15.已知a,b为正实数,且 ,则 的最小值为( )
A.1 B.6 C.7 D.
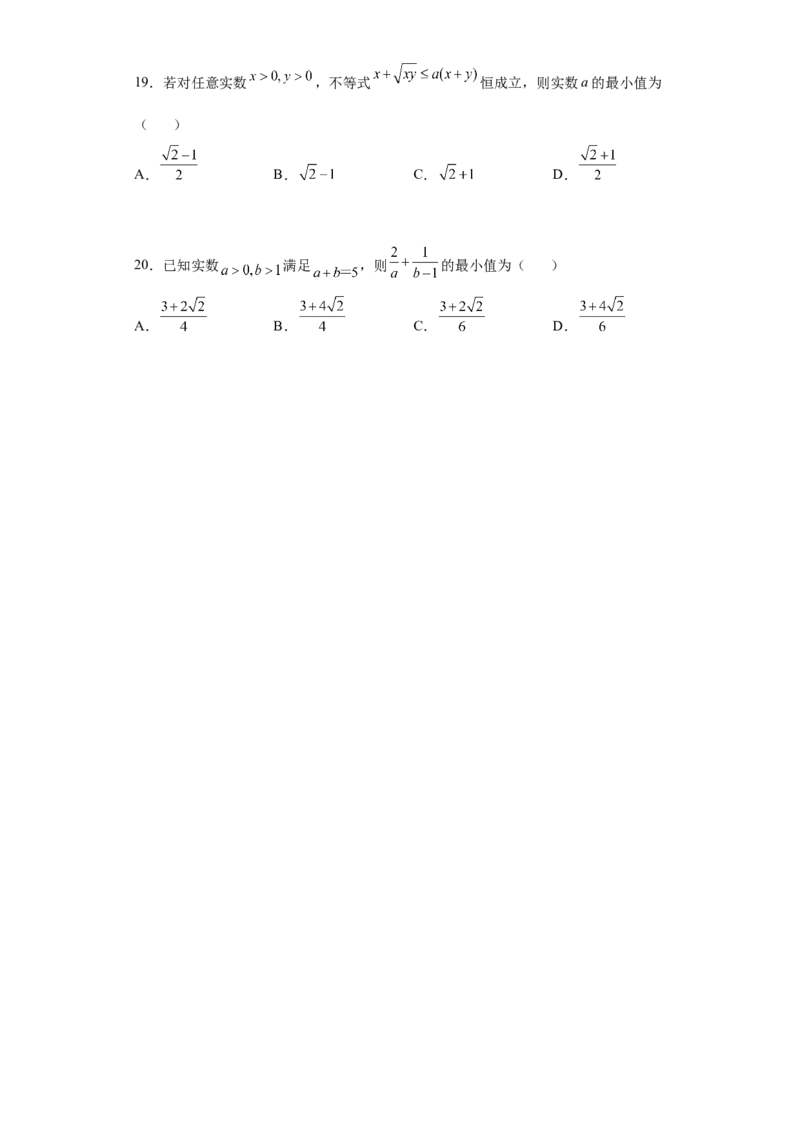
16.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学
家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实
现证明,也称之为无字证明.现有如图所示图形,点 在半圆 上,点 在直径
上,且 ,设 , ,则该图形可以完成的无字证明为( )
A. B.
C. D.
17.若 , ,则 的最小值是( )
A.16 B.18 C.20 D.22
18.已知实数 , 满足 ,则 的最小值为( )
A. B.
C. D.19.若对任意实数 ,不等式 恒成立,则实数a的最小值为
( )
A. B. C. D.
20.已知实数 满足 ,则 的最小值为( )
A. B. C. D.