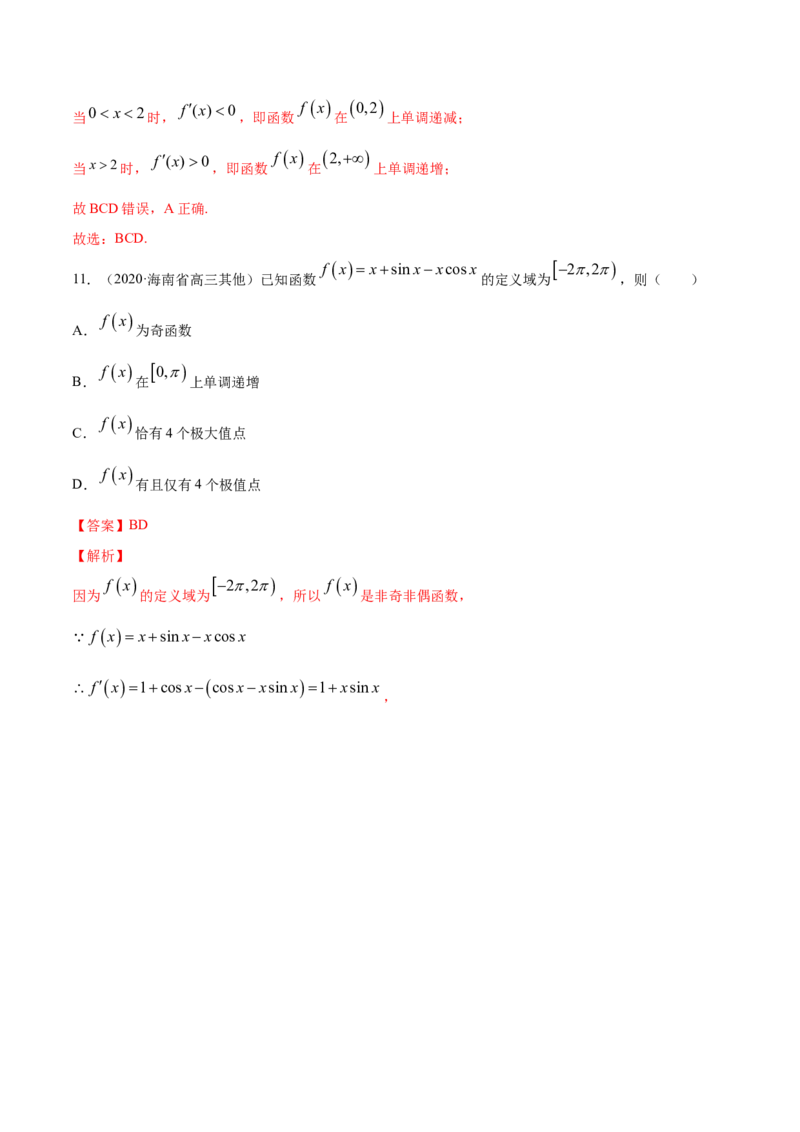专题23导数在研究函数中的应用（1）（解析版）_E015高中全科试卷_数学试题_选修2_06.专项练习_专题23导数在研究函数中的应用（1）-高中数学新教材人教A版选择性必修配套提升训练

专题23 导数在研究函数中的应用（1） 一、单选题 f x a,b f x a,b 1．（2020·江西省奉新县第一中学高二月考（理））函数 的定义域为 ，导函数 在 f x a,b 内的图象如图所示．则函数 在 内有几个极小值点（ ） A．1 B．2 C．3 D．4 【答案】A 【解析】 因为极小值点两侧函数的单调性是先减后增，对应导函数值是先负后正， 由图得：导函数值先负后正的点只有一个， f x a,b 故函数 在 内极小值点的个数是1. 故选：A y  f(x) y  f(x) 2．（2020·江西省奉新县第一中学高二月考（理））将 和 的图象画在同一个直角坐标 系中，不可能正确的是( ) A． B． C． D． 【答案】D 【解析】fx0 f x fx0 f x 根据 ，则 单调递增； ， 单调递减， A,B,C 容易判断 正确； 对选项D：取 fx 与 x 轴的两个交点的横坐标为 m,n x,n fx0 数形结合可知当 时， ， f x 故此时函数 应该在此区间单调递减， f x 但从图象上看 不是单调递减函数，故该选项错误. 故选：D. y  f x y  fx 3．（2020·蚌埠田家炳中学高二开学考试（理））如图是函数 的导函数 的图象，下列 y  f x 关于函数 的极值和单调性的说法中，正确的个数是（ ） x x x y  f x ① 2， 3， 4都是函数 的极值点； x x y  f x ② 3， 5都是函数 的极值点； y  f(x) (x x ) ③函数 在区间 1， 3 上是单调的；y  f(x) (x x ) ④函数 在区间上 3， 5 上是单调的． A．1 B．2 C．3 D．4 【答案】C 【解析】 f(x) (,x ) (x x ) (x ) 由图象得： 在 3 递增，在 3， 5 递减，在 5， 递增， x x y  f(x) 故 3， 5都是函数 的极值点， 故②③④正确， 故选：C． y  f x y  f 'x 4．（2020·鸡泽县第一中学高二开学考试）如图是函数 的导数 的图象，则下面判断正 确的是（ ） 3,1 f x A．在 内 是增函数 f x x1 B．在 时 取得极大值 4,5 f x C．在 内 是增函数 f x x2 D．在 时 取得极小值 【答案】C 【解析】 y  f(x) (3,1)  (3,1) 对A，由导函数 的图象可知，在区间 内函数先减后增， 在 不单调，故A错误； x1 f '(1)0 f(1) 对B，当 时， ，此时 不是极大值，故B错误；(4,5) f(x)0 对C，在 内 ，此时函数单调递增，故C正确． x2 f '(2)0 f(2) 对D，当 时， ，但此时 不是极小值，而是极大值，故D错误； 故选：C． f x xxc2 5．（2020·黄冈中学第五师分校高二期中（理））已知函数 在x2处取得极大值，则c 的值为（ ） A．2 B．6 C．4 D．4 【答案】B 【解析】 fxxc2 2xxc 由题意得： ， f22c2 222c0 由 ，解得：c6或c2. fxx63x6 当c6时， ， x,2 fx0 f x x2,6 fx0 f x 当 时， ， 单调递增；当 时， ， 单调递减； f x  在 x2 处取得极大值，符合题意； fxx23x2 c2 当 时， ， 3  x ,2  当  2  时， fx0， f x 单调递减；当x2, 时， fx0， f x 单调递增； f x  在 x2 处取得极小值，不合题意； 综上所述：c6. 故选：B. f(x) x3ax2 bx x1 6．（2020·蚌埠田家炳中学高二开学考试（理））已知函数 在 处有极值10，则 f(2) 等于( ) A．1 B．2 C．—2 D．—1【答案】B 【解析】 f x x3ax2 bx  ，  f 'x3x2 2axb ， f x x3ax2 bx x1 函数 在 处有极值为10， 32ab0 a 12   1ab10 ，解得 b21 ． a12, b21 经检验知， 符合题意．  f x x312x2 21x ，  f 2231222 2122 ．选B． 点睛： 由于导函数的零点是函数极值点的必要不充分条件，故在求出导函数的零点后还要判断在该零点两侧导函 x 数的值的符号是否发生变化，然后才能作出判断．同样在已知函数的极值点 0求参数的值时，根据 f(x )0 0 求得参数的值后应要进行检验，判断所求参数是否符合题意，最终作出取舍．   a  f log 3 7．（2020·江西省石城中学高二月考（文））已知函数 f x xsinx， ，若 1 ， xR   2   b f   log 1 2  ，c f  22则 a,b,c 的大小为（ ） 3 abc bca cba bac A． B． C． D． 【答案】C 【解析】f xxsinx f'x1cosx0 ，所以 f x 是R上的增函数. log 3log 3log 21,0log 2log 2log 31,22 0  1 2 2 1 3 3 ， 2 3     c f  22 b f log 2a f log 3 所以 1 1 ，故本题选C.     3 2 1 f(x)lnxax [1,) 8.（2020·蚌埠田家炳中学高二开学考试（理））若函数 x 在 上是单调函数， 则a的取值范围是（ ） 1   1 (,0]  , [0,)     A． 4  B． 4  1   ,0   C． 4  D．(,1] 【答案】B 【解析】 1 1  a 由题意得，f′（x） x x2 ， 1 f xlnxax 因为 x 在[1，+∞）上是单调函数， 所以f′（x）≥0或f′（x）≤0在[1，+∞）上恒成立， 1 1 a 0 ①当f′（x）≥0时，则 x x2 在[1，+∞）上恒成立， 1 1 1 1 1 1 1     (  )2  即a x2 x ，设g（x） x2 x x 2 4 ， 1 因为x∈[1，+∞），所以 x ∈（0，1]，1  当 x 1时，g（x）取到最大值是：0， 所以a≥0， 1 1 a 0 ②当f′（x）≤0时，则 x x2 在[1，+∞）上恒成立， 1 1 1 1 1 1 1     (  )2  即a x2 x ，设g（x） x2 x x 2 4 ， 1 因为x∈[1，+∞），所以 x ∈（0，1]， 1 1 1   当 x 2 时，g（x）取到最大值是： 4 ， 1  所以a 4， 1  综上可得，a 4或a≥0， 1  所以数a的取值范围是（﹣∞， 4 ]∪[0，+∞）， 故选：B． 二、多选题 y  f x 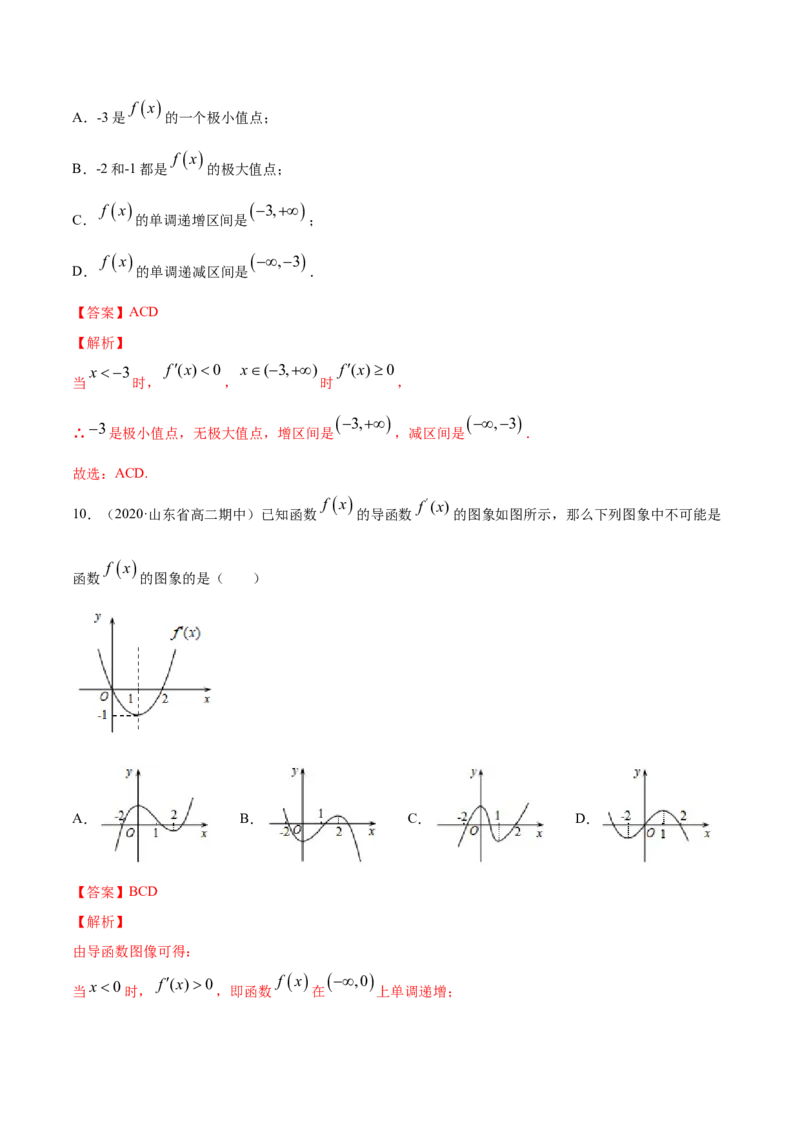9．（2020·江苏省扬州中学高二期中）定义在R上的可导函数 的导函数的图象如图所示，以下 结论正确的是（ ）f x A．-3是 的一个极小值点； f x B．-2和-1都是 的极大值点； f x 3, C． 的单调递增区间是 ； f x ,3 D． 的单调递减区间是 ． 【答案】ACD 【解析】 x3 f(x)0 x(3,) f(x)0 当 时， ， 时 ， 3, ,3 3 ∴ 是极小值点，无极大值点，增区间是 ，减区间是 ． 故选：ACD. f x f(x) 10．（2020·山东省高二期中）已知函数 的导函数 的图象如图所示，那么下列图象中不可能是 f x 函数 的图象的是（ ） A． B． C． D． 【答案】BCD 【解析】 由导函数图像可得： x0 f(x)0 f x ,0 当 时， ，即函数 在 上单调递增；0 x2 f(x)0 f x 0,2 当 时， ，即函数 在 上单调递减； f(x)0 f x 2, 当x2时， ，即函数 在 上单调递增； 故BCD错误，A正确. 故选：BCD. 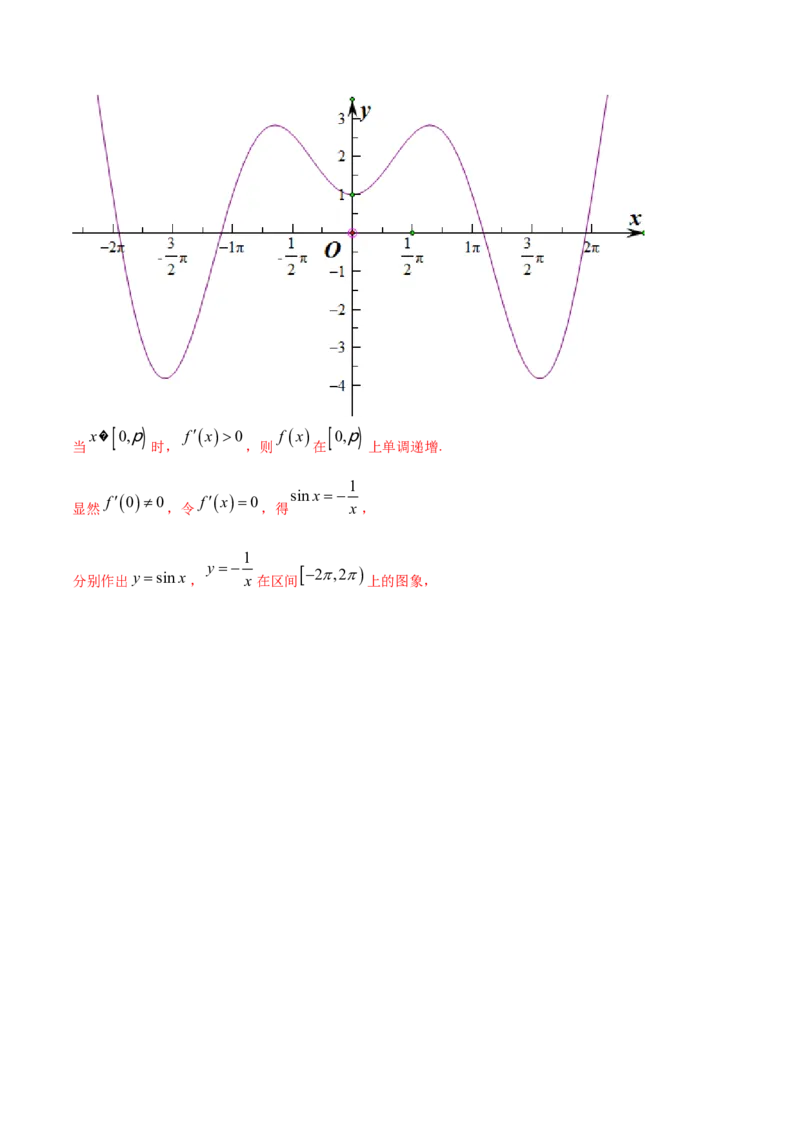f x xsinxxcosx 2,2 11．（2020·海南省高三其他）已知函数 的定义域为 ，则（ ） f x A． 为奇函数 f x 0, B． 在 上单调递增 f x C． 恰有4个极大值点 f x D． 有且仅有4个极值点 【答案】BD 【解析】 f x 2,2 f x 因为 的定义域为 ，所以 是非奇非偶函数， f x xsinxxcosx   fx1cosxcosxxsinx1xsinx ，x�[0,p) fx0 f x [0,p) 当 时， ，则 在 上单调递增. 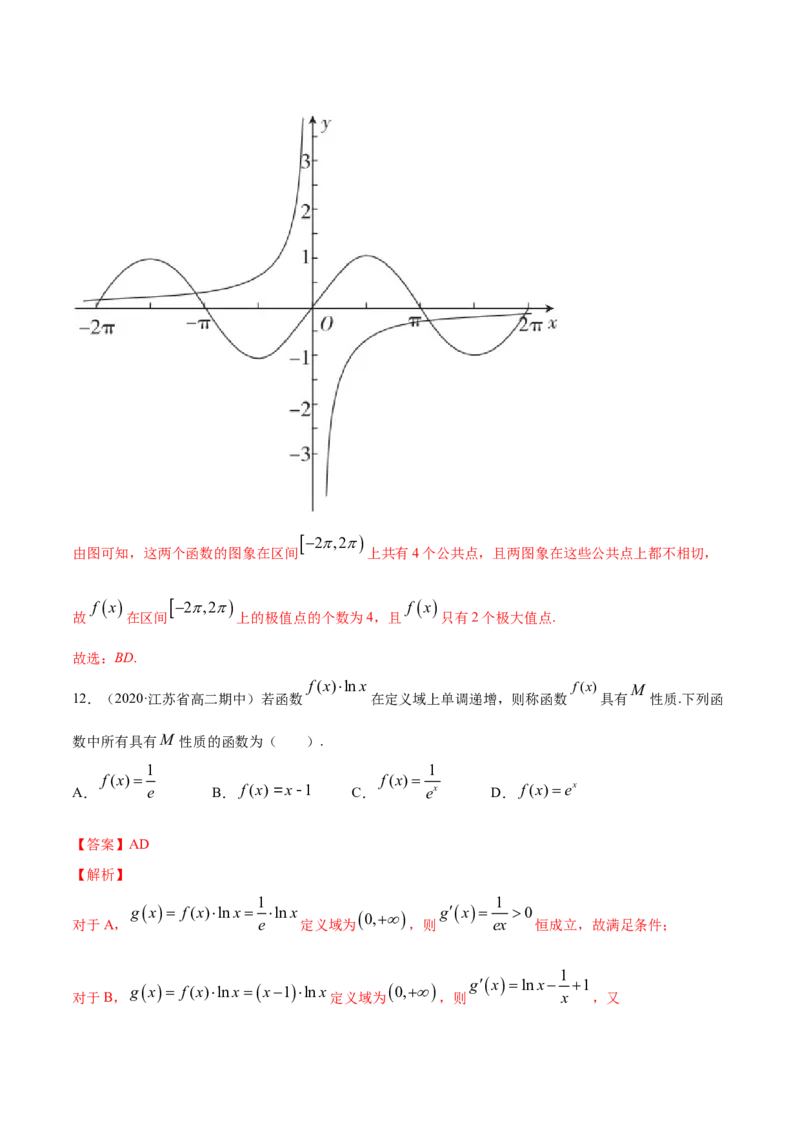1 f00 fx0 sinx 显然 ，令 ，得 x ， 1 分别作出y sinx， y  x 在区间 2,2 上的图象，2,2 由图可知，这两个函数的图象在区间 上共有4个公共点，且两图象在这些公共点上都不相切， f x 2,2 f x 故 在区间 上的极值点的个数为4，且 只有2个极大值点. 故选：BD. f(x)lnx f(x) M 12．（2020·江苏省高二期中）若函数 在定义域上单调递增，则称函数 具有 性质.下列函 数中所有具有M 性质的函数为（ ）. 1 1 f(x) f(x) A． e B． f(x)=x-1 C． ex D． f(x)ex 【答案】AD 【解析】 1 1 gx f(x)lnx lnx 0, gx 0 对于A， e 定义域为 ，则 ex 恒成立，故满足条件； 1 gx f(x)lnxx1lnx 0, gxlnx 1 对于B， 定义域为 ，则 x ，又  1  1 1 1   lnx x 1    x  x2 0 ，g1ln1 1 10，即当 0 x1 时 gx0 ，函数 gx在0,1上 x1 gx0 gx 1, 单调递减，当 时 ，函数 在 上单调递增，故不满足条件； 1 lnx 对于C， gx f(x)lnx 1 lnx 定义域为 0, ， gx x ，又 ex ex 1  1 1  1 1   x lnx    x2  x 0，即 gx 在定义域上单调递减，且 ge e ee 0 ，故不满足函数 gx 在 定义域上单调递增，故错误； 1  1 gxexlnx ex ex lnx 对于D，gx f(x)lnxexlnx定义域为 0, ， x   x  ，令 1 1 1 x1 hxlnx hx   x ， x x2 x2 ， x1 hx0 0 x1 hx0 hx 0,1 1, 则 时， ；当 时 ，即 在 上单调递减，在 上单调递增，  1 gxex lnx 0 在x1处取得极小值即最小值hx h110，所以   x   恒成立，即gx min 在定义域上单调递增，故D正确； 故选：AD 三、填空题 f(x) x33x2 5 13．（2020·江苏省邗江中学高一期中）函数 的极小值为_______________． 【答案】1 【解析】 f(x) x33x2 5 f'(x)3x2 6x 3xx2 ，故 ，f '(x)0 0 x2 0,2 取 得到 ，故函数在 上单调递减； 取 f '(x)0 得到x2或 x0 ，故函数在 ,0 和 2, 上单调递增. f(2)1 故极小值为 . 故答案为：1. 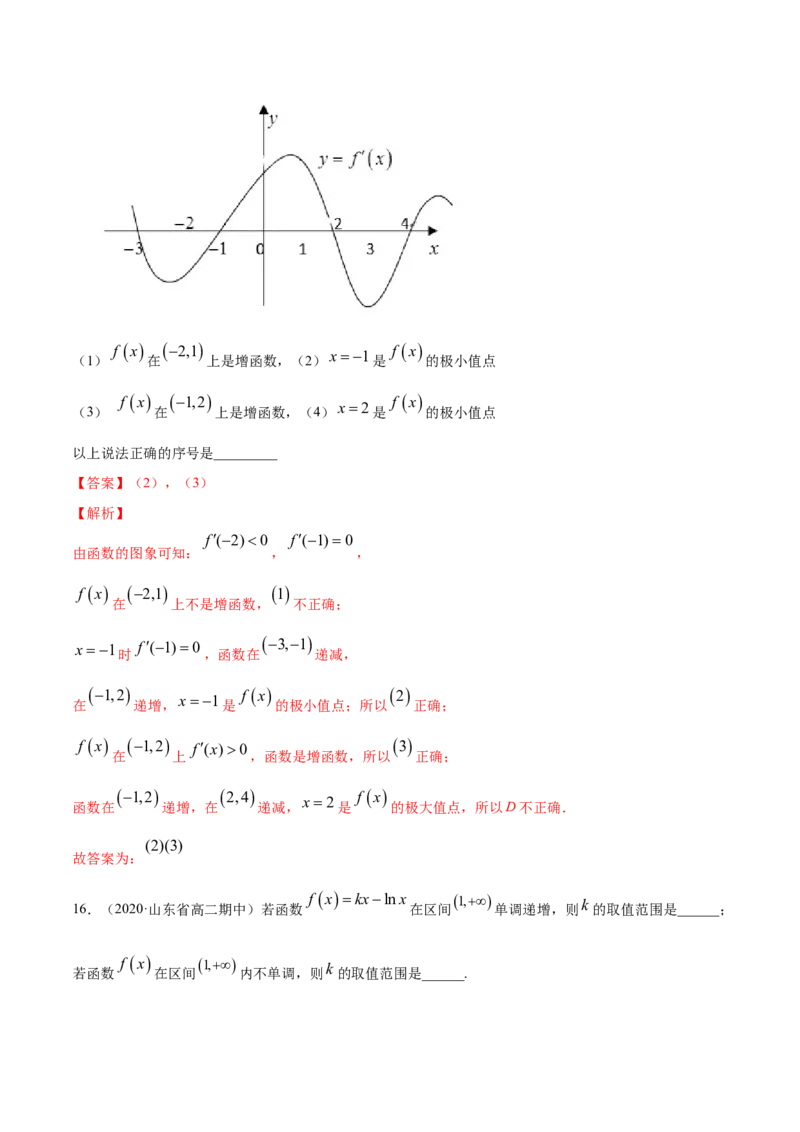y  f xxR 14．（2020·蚌埠田家炳中学高二开学考试（理））已知函数 的图象如图所示，则不等式 xf 'x0 的解集为______．  1  0，2，   【答案】 2 ． 【解析】 y  f x 由 图象特征可得， 1 1 f x (, ]  [2,) fx0 ( ,2) fx0 导数 ，在 2 上 ，在 2 上 ， x0 x0 1 所以xfx0等价于  fx0或  fx0，解得0 x 或 ，   2 x2 1 xfx0 [0, ][2,) 即不等式 的解集为 2 ． y  f x 15．（2020·周口市中英文学校高二月考（理））如图是 的导函数的图象，现有四种说法．f x 2,1 f x x1 （1） 在 上是增函数，（2） 是 的极小值点 f x 1,2 f x x2 （3） 在 上是增函数，（4） 是 的极小值点 以上说法正确的序号是_________ 【答案】（2），（3） 【解析】 f(2)0 f(1)0 由函数的图象可知： ， ， f x 2,1 1 在 上不是增函数， 不正确； x1 f(1)0 3,1 时 ，函数在 递减， 1,2 f x 2 x1 在 递增， 是 的极小值点；所以 正确； f x 1,2 f(x)0 3 在 上 ，函数是增函数，所以 正确； 1,2 2,4 f x x2 函数在 递增，在 递减， 是 的极大值点，所以D不正确． (2)(3) 故答案为： f xkxlnx 1, k 16．（2020·山东省高二期中）若函数 在区间 单调递增，则 的取值范围是______； f x 1, k 若函数 在区间 内不单调，则 的取值范围是______.1, 0,1 【答案】 【解析】 1 若 f xkxlnx 在区间 1, 单调递增，所以 fxk x 0 在 1, 上恒成立， 1 1 k  1 即 x 在 1, 上恒成立，又x1时， x ，所以k�1； 1 若函数 f x 在区间 1, 内不单调，则方程 fxk x 0 在区间 1, 有解， 1 0 1 因为x1时， x ，因此只需0k 1. 1, 0,1 故答案为： ； . 四、解答题 f(x) xex 17．（2020·横峰中学高二开学考试（文））已知函数 ． y  f(x) (1, f(1)) （1）求曲线 在点 处的切线方程； f(x) （2）求函数 的极值． 1  【答案】（1）2ex ye0；（2）极小值为 e，无极大值． 【解析】 f(x) xex f(1)e 1,e （1） ，则 ，切点坐标为 ． f(x) xex ex (x1)ex 由题意知， ， k  f(1)2e ye2e(x1) ，由直线的点斜式方程有： 2ex ye0 即 ．f(x)(x1)ex （2）由（1）知， ， f(x)0 x1 f(x)0 x1 令 ，得 ；令 ，得 ． f(x) (,1) (1,) 则 在 上单调递减，在 上单调递增， 1 f(1) 所以 f(x)的极小值为 e ，无极大值． f(x) x2 2(a1)x2alnx(a 0) 18．（2020·黄冈中学第五师分校高二期中（理））已知函数 . y  f(x) (1, f(1)) a1 （1）当 时，求曲线 在点 处的切线方程； f(x) （2）求 的单调区间； y 3 【答案】（1） （2）详见解析 【解析】 2  fx2x4  f x x2 4x2lnx （1） a1， ， x ，   f10 f 1143 ，又 ，  f x  1, f 1 y 3 在 处的切线方程为 . 2a 2x2 2a1x2a 2xax1 fx2x2a1   x0 （2） x x x ， fx0 x a x 1 令 ，解得： 1 ， 2 . 0a1 x0,a 1, fx0 xa,1 fx0 ①当 时，若 和 时， ；若 时， ；  f x 0,a 1, a,1 的单调递增区间为 ， ；单调递减区间为 ； fx0 0, ②当a1时， 在 上恒成立， f x 0, 的单调递增区间为 ，无单调递减区间； x0,1 a, fx0 x1,a fx0 ③当a1时，若 和 时， ；若 时， ；  f x 0,1 a, 1,a 的单调递增区间为 ， ；单调递减区间为 ； 0a1 f x 0,a 1, a,1 综上所述：当 时， 的单调递增区间为 ， ；单调递减区间为 ； f x 0, 当a1时， 的单调递增区间为 ，无单调递减区间； f x 0,1 a, 1,a 当a1时， 的单调递增区间为 ， ；单调递减区间为 . 1 f xax2 blnx 19．（2020·阳江市第三中学高二期中）已知函数 在x1处有极值2 ． （1）求a,b的值； f x （2）求 的单调区间． 1 a 0,1 1, 【答案】(1) 2,b1．(2) 单调减区间是 ,单调增区间是 ． 【解析】 b 1  f 'x2ax . f x （1） x 又 在x1处有极值2 ,  1  1 f 1 a   2  2 1 即 解得 , ．   f '10  2ab0 a  2 b1 1 f x x2 lnx 0, （2）由（1）可知 2 ,其定义域是 , 1 x1x1 f 'x x  x x ． f 'x0 f 'x0 0 x1 x1 由 ,得 ；由 ,得 ．y  f x 0,1 1, 函数 的单调减区间是 ,单调增区间是 ． 2 x 20．（2020·山东省高二期中）已知函数 f(x)ax3 x2 bx在 3与x1时都取得极值. a b （1）求 ， 的值；  2 f  （2）求函数 f x 的单调区间，并指出   3  与 f 1 是极大值还是极小值.  2 , 【答案】（1）a2， b4 .（2）函数 f x 的单调递增区间是   3  和1,，单调递减区间是  2   2  ,1 f       3 ，  3是极大值， f(1)是极小值 【解析】 f xax3 x2 bx f 'x3ax2 2xb （1）由 ，所以 .  2 f  0   由题意可知  3 ， f(1)0， 4 4  ab 0 3 3 整理列方程组  3ab20 a2 b4 解得 ， . fx6x2 2x423x2x1 （2）由（1）知 f 'x f x x 当 变化时， ､ 的变化情况如下表：  2 2  2  x  ,     ,1  1 1,  3 3  3  f 'x + 0 - 0 +f(x) 单调递增 极大值 单调递减 极小值 单调递增     2  2  ,  ,1 所以函数 f x 的单调递增区间是   3  和1,，单调递减区间是   3   2  2 44 x f     当 3时， f(x)有极大值  3 27 ； x1 f(x) f(1)3 当 时， 有极小值 . 21．（2020·江苏省扬州中学高二期中）已知函数f（x）＝ax3+bx2﹣3x在x＝﹣1和x＝3处取得极值. （1）求a，b的值 （2）求f（x）在[﹣4，4]内的最值. 1 76 5   【答案】（1）a 3，b＝﹣1（2）f（x） ＝ 3 ，f（x） ＝3 min max 【解析】 f '(x) （1） ＝3ax2+2bx﹣3， f '(x) 由题意可得 ＝3ax2+2bx﹣3＝0的两个根为﹣1和3，  2b 13   3a  则 1 ，  13  a 1  解可得a 3，b＝-1， f '(x)＝(x﹣3)(x1) （2）由（1） ， (-, -1) (3,) (1,3) 易得f（x）在 ， 单调递增，在 上单调递减， 76 5 20    又f（﹣4） 3 ，f（﹣1） 3，f（3）＝﹣9，f（4） 3 ，76 5   所以f（x） ＝f（﹣4） 3 ，f（x） ＝f（﹣1） 3. min max f x x2 8lnx 22．（2020·安徽省池州一中高二期中（文））已知函数 f x ; （1）求函数 的极值 1  ,e （2）求函数 f x 在区间  e  上的最值． 1 8 【答案】（1）极小值为48ln2；无极大值（2）最小值为48ln2，最大值为e2 ． 【解析】 8 2x2x2 （1）由题意得： f x 定义域为 0, ， fx2x x  x ， x0,2 fx0 x2, fx0 当 时， ；当 时， ，  f x 0,2 2, 在 上单调递减，在 上单调递增，  f x f 248ln2 的极小值为 ，无极大值； 1  ,2 （2）由（1）知： f x 在  e   上单调递减，在 2,e 上单调递增，  1   f x  f 248ln2， f x max max  f  e   , f e   ， min 1 1 1 1 1 f  8  f  f e  f x  f  8 又  e   e2 ， f ee2 8，  e   ， max  e   e2 .