文档内容
章末检测(五) 三角函数 能力卷
(时间:120分钟,满分:150分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选
项是符合题目要求的.
1.(2019·广东省高一月考)角 弧度,则 所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【解析】角 弧度, ,∴α在第三象限,故选:C.
2.(2020·北京高三二模)《九章算术》成书于公元一世纪,是中国古代乃至东方的第一部自成体
系的数学专著.书中记载这样一个问题“今有宛田,下周三十步,径十六步.问为田几何?”(一步
=1.5米)意思是现有扇形田,弧长为45米,直径为24米,那么扇形田的面积为( )
A.135平方米 B.270平方米 C.540平方米 D.1080平方米
【答案】B
【解析】根据扇形的面积公式,计算扇形田的面积为S lr 45 270(平方米).故选:
B.
3.(2020·辽宁省沈阳铁路实验中学高一期中)如果角 的终边过点 ,那
么 等于( )
A. B. C. D.
【答案】C【解析】由题意得 ,它与原点的距离为2,∴ .故选:C.
4.(2020·湖南省高一月考)设 ,则 的大小关系为(
)
A. B. C. D.
【答案】C
【解析】以 为圆心作单位圆,与 轴正半轴交于点 ,作 交单位圆第一象限于点 ,
做 轴,作 轴交 的延长线于点 ,如下图所示:
由三角函数线的定义知, , , ,因为 ,
∴ ∴ 故选:C
5.(2019·陕西省高三月考(理))定义运算: ,将函数的图像向左平移 个单位,所得图像对应的函数为偶函数,则 的
最小值是( )
A. B. C. D.
【答案】C
【解析】 ,将函数 化为
再向左平移 ( )个单位即为:
又为偶函数,由三角函数图象的性质可得,即 时函数值为最大或
最小值,即 或 ,所以 ,即
,又 ,所以 的最小值是 .
6.(2020·高唐县第一中学高一月考)已知 , ,则 的
值为( )A. B. C. D.
【答案】B
【解析】由 , ,
联立方程组,可得 ,
又由 .故选:B.
7.(2020·四川省高三三模(理))设函数 与函数
的对称轴完全相同,则 的值为( )
A. B. C. D.
【答案】C
【解析】由题意,求函数 的对称轴,令 ,
解得 函数 ,
令 ,解得 ,因为函数 与函数 的对称轴完全相
同,所以 ,故选:C.
8.(2019·云南省东川明月中学高一期中)函数 ,若对
于任意的 有 恒成立,则实数 的取值范围是( ).
A. B. C. D.
【答案】D
【解析】
, ,
最小值
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得5分,部分选对的得3分,有选错的得0分.
9.(2020·全国高一课时练习)(多选题)已知 ,则下列式子成立的是(
)A. B.
C. D.
【答案】CD
【解析】∵ , ,
整理得 ,
∴ ,
即 ,
即 ,∴C、D正确.故选:CD
10.(2019·全国高一课时练习)(多选)下列命题中,真命题的是( )
A. 的图象与 的图象关于 轴对称
B. 的图象与 的图象相同
C. 的图象与 的图象关于 轴对称
D. 的图象与 的图象相同
【答案】BD
【解析】对于A, 是偶函数,而 为奇函数,故 与 的图象不关
于 轴对称,故A错误;对于B, ,即其图象相同,故B正确;
对于C,当 时, ,即两图象相同,故C错误;
对于D, ,故这两个函数图象相同,故D正确,故选BD.
11.(2020·全国高一课时练习)定义:角 与 都是任意角,若满足 ,则称 与 “广
义互余”.已知 ,则下列角 中,可能与角 “广义互余”的是( )
A. B. C. D.
【答案】AC
【解析】∵ ,∴ ,若 ,则 .
A中, ,故A符合条件;
B中, ,故B不符合条件;
C中, ,即 ,
又 ,所以 ,故C符合条件;D中, ,即 ,
又 ,所以 ,故D不符合条件.故选:AC.
12.(2020·山东省高一期末)对于函数 ,下列四个结论正确的是(
)
A. 是以 为周期的函数
B.当且仅当 时, 取得最小值-1
C. 图象的对称轴为直线
D.当且仅当 时,
【答案】CD
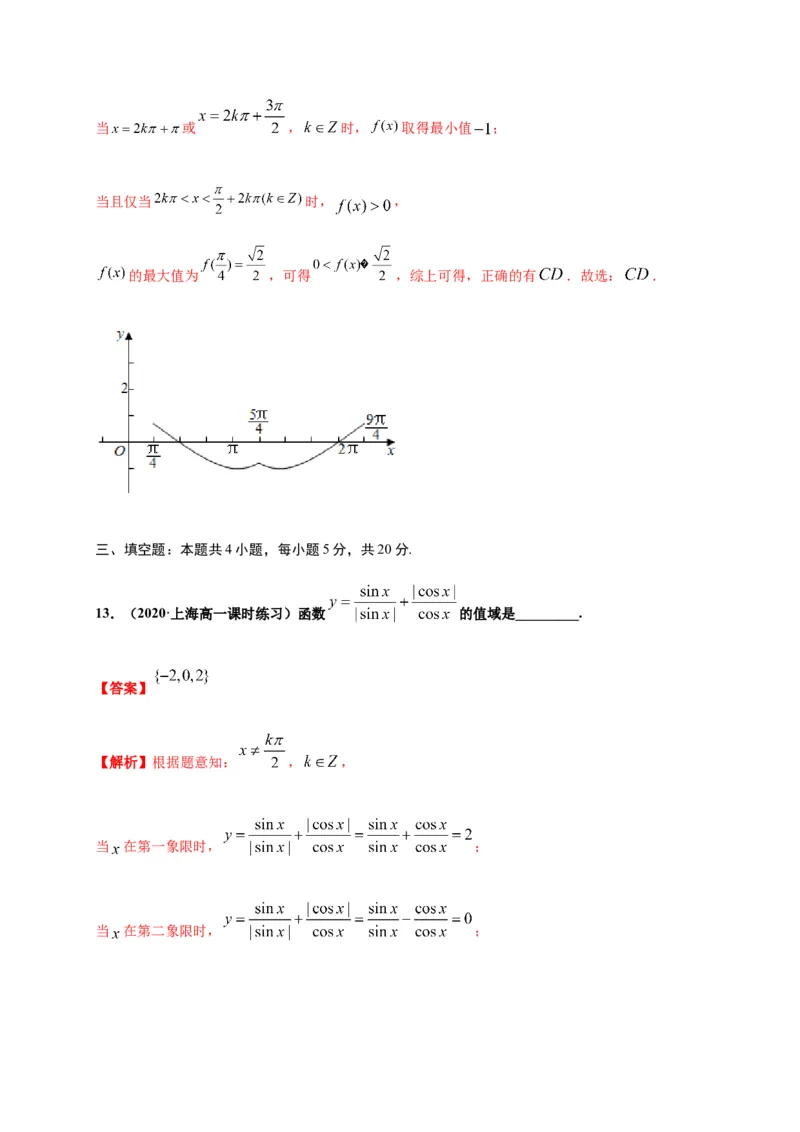
【解析】函数 的最小正周期为 ,画出 在一个周期内的图象,
可得当 , 时, ,
当 , 时, ,
可得 的对称轴方程为 , ,当 或 , 时, 取得最小值 ;
当且仅当 时, ,
的最大值为 ,可得 ,综上可得,正确的有 .故选: .
三、填空题:本题共4小题,每小题5分,共20分.
13.(2020·上海高一课时练习)函数 的值域是_________.
【答案】
【解析】根据题意知: , ,
当 在第一象限时, ;
当 在第二象限时, ;当 在第三象限时, ;
当 在第四象限时, ;
综上所述:值域为 .
14.(2020·上海高一课时练习)若函数 的最小值为1,则实数
__________.
【答案】5
【解析】 ,其中 ,且 终边过点
.所以 ,解得 .
15.(2020·江苏省高三其他)已知函数 ( ),且
( ),则 ______.
【答案】
【解析】解法一:∵函数 ( ), .
,( ),不妨假设 ,则 , ,
,
, , .
再根据
,
,或 ,则 (舍去)或 ,
解法二:∵函数 ( ), .
( ),
则由正弦函数的图象的对称性可得: ,即 ,
16.(2020·浙江省高三二模)已知函数 的图像关于点
对称,关于直线 对称,最小正周期 ,则 ______, 的单调递减区间是______.
【答案】
【解析】由于 的最小正周期 , ,所以 .
由于 图像关于点 对称,关于直线 对称,
所以 ,
两式相加得 ,
由于 , ,所以 .
则 ,结合 可得 ,
所以 .
所以 的最小正周期为 .
由 ,解得 ,所以 的减区间为.
故答案为:(1) ;(2)
五、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)17.(2020·甘肃省静宁县第一中学高一月考(理))已知
.
(1)求 的值
(2)求 的值.
【解析】(1)∵ .
∴ ,即
,
(2)由(1)知 <0,又∴
∴
18.(2019·瓦房店市实验高级中学高一月考)函数 的
一段图象如图所示
(1)求 的解析式;
(2)求 的单调增区间,并指出 的最大值及取到最大值时 的集合;
(3)把 的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.
【解析】(1)由函数的图象可得 ,解得 .
再根据五点法作图可得 ,由 ,则令
(2)令 ,求得 ,故函数的增区间为[
函数的最大值为3,此时, ,即 ,即 的最大值为
3,及取到最大值时 的集合为 .
(3)设把 的图象向左至少平移m个单位,才能使得到的图象对应的函数
为偶函数.
则由 ,求得 ,
把函数 的图象向左平移 个单位,
可得 的图象.
19.(2020·北京高三二模)已知函数 ,
,求 在 的值域.
从①若 的最小值为 ;② 两条相邻对称轴之间的距离为 ;③若 的最小值为 ,这三个条件中任选一个,补充在上面问题中并作答.
【解析】由于
.
所以①②③都可以得到 的半周期为 ,则 .
所以 .由于 , ,
所以 ,即 的值域为 .
20.(2020·广东省高一月考)已知函数 .
(1)求 的最小正周期;
(2)若 ,求 的值.
【解析】(1)
,
∴ .(2)∵ , , ,
∴ .
21.(2020·安徽省六安一中高一期末(理))已知函数 ,
其中 .
(1)求使得 的 的取值范围;
(2)若函数 ,且对任意的 ,当 时,均有
成立,求正实数 的最大值.
【解析】(1)由题意得,
令 ,得
即 ,故 的取值范围为
(2)由题意得,
令即 故 在区间 上为增函数
由 , 得出, ,
则函数 包含原点的单调递增区间为 即
故正实数 的最大值为 .
22.(2019·江苏省高二期末(文))某班级欲在半径为1米的圆形展板上做班级宣传,设计方案
如下:用四根不计宽度的铜条将圆形展板分成如图所示的形状,其中正方形ABCD的中心在展板圆
心,正方形内部用宣传画装饰,若铜条价格为10元/米,宣传画价格为20元/平方米,展板所需总
费用为铜条的费用与宣传画的费用之和.
(1)设 ,将展板所需总费用表示成 的函数;
(2)若班级预算为100元,试问上述设计方案是否会超出班级预算?
【解析】(1)过点O作 ,垂足为H,则 , ,正方形ABCD的中心在展板圆心, 铜条长为相等,每根铜条长 ,
, 展板所需总费用为 .
(2)
,当 时等号成立.
上述设计方案是不会超出班级预算.