专题23导数在研究函数中的应用（1）（原卷版）_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_高中数学新教材人教A版选择性必修配套提升训练(等10份资料)

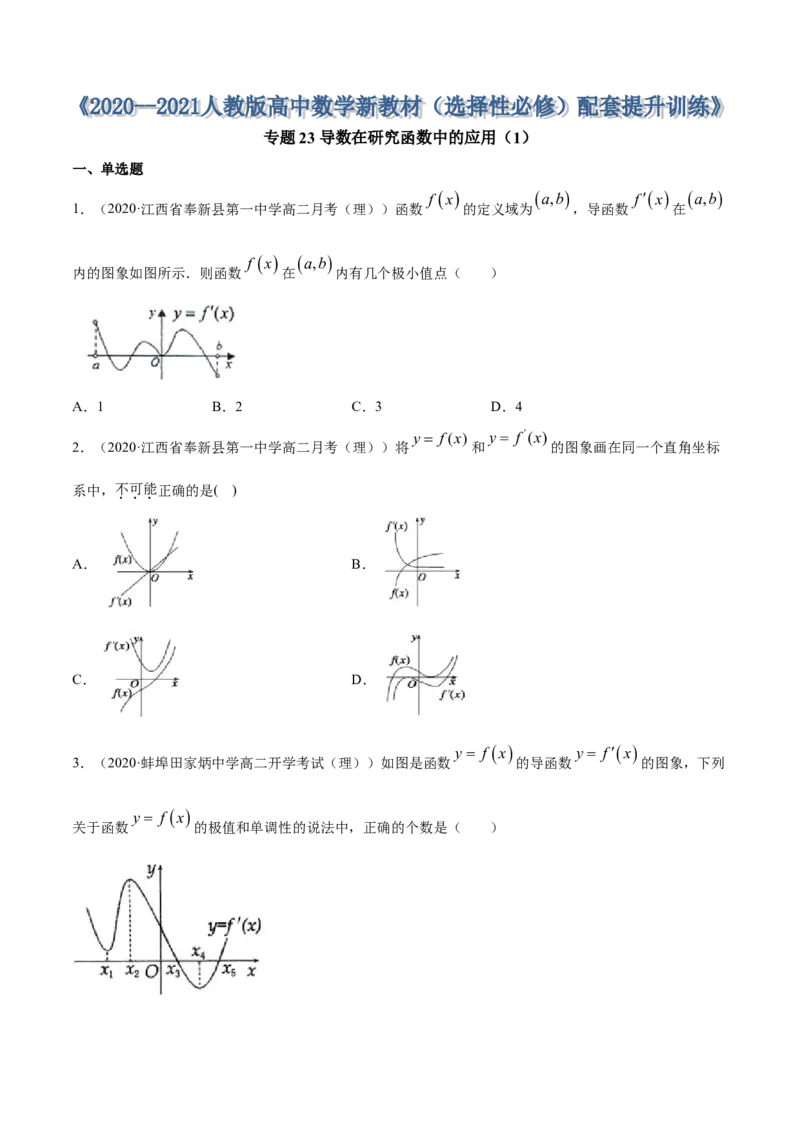
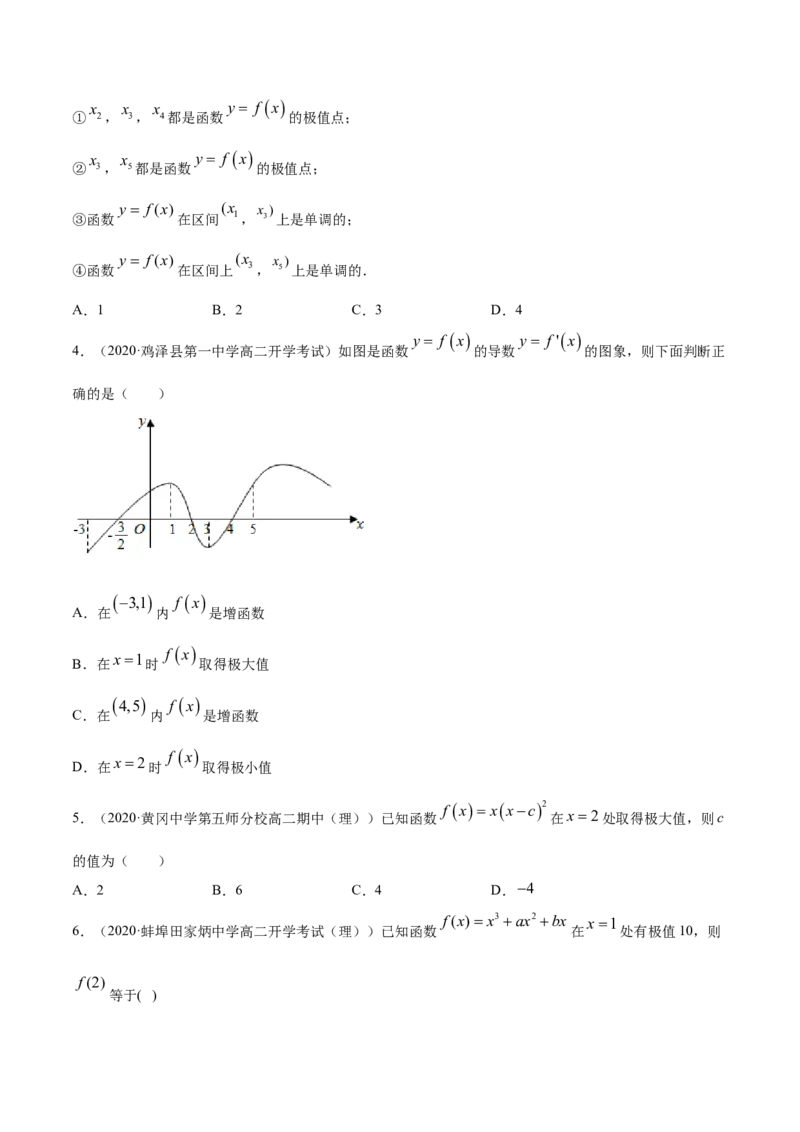
专题23 导数在研究函数中的应用（1） 一、单选题 f x a,b f x a,b 1．（2020·江西省奉新县第一中学高二月考（理））函数 的定义域为 ，导函数 在 f x a,b 内的图象如图所示．则函数 在 内有几个极小值点（ ） A．1 B．2 C．3 D．4 y  f(x) y  f(x) 2．（2020·江西省奉新县第一中学高二月考（理））将 和 的图象画在同一个直角坐标 系中，不可能正确的是( ) A． B． C． D． y  f x y  fx 3．（2020·蚌埠田家炳中学高二开学考试（理））如图是函数 的导函数 的图象，下列 y  f x 关于函数 的极值和单调性的说法中，正确的个数是（ ）x x x y  f x ① 2， 3， 4都是函数 的极值点； x x y  f x ② 3， 5都是函数 的极值点； y  f(x) (x x ) ③函数 在区间 1， 3 上是单调的； y  f(x) (x x ) ④函数 在区间上 3， 5 上是单调的． A．1 B．2 C．3 D．4 y  f x y  f 'x 4．（2020·鸡泽县第一中学高二开学考试）如图是函数 的导数 的图象，则下面判断正 确的是（ ） 3,1 f x A．在 内 是增函数 f x x1 B．在 时 取得极大值 4,5 f x C．在 内 是增函数 f x x2 D．在 时 取得极小值 f x xxc2 5．（2020·黄冈中学第五师分校高二期中（理））已知函数 在x2处取得极大值，则c 的值为（ ） A．2 B．6 C．4 D．4 f(x) x3ax2 bx x1 6．（2020·蚌埠田家炳中学高二开学考试（理））已知函数 在 处有极值10，则 f(2) 等于( )A．1 B．2 C．—2 D．—1   a f log 3 7．（2020·江西省石城中学高二月考（文））已知函数 f x xsinx， ，若 1 ， xR   2   b f log 1 2 ，c f  22则 的大小为（ ）   a,b,c 3 abc bca cba bac A． B． C． D． 1 f(x)lnxax 8.（2020·蚌埠田家炳中学高二开学考试（理））若函数 x 在[1,)上是单调函数，则a 的取值范围是（ ） 1   1 (,0]  , [0,)     A． 4  B． 4  1   ,0   C． 4  D．(,1] 二、多选题 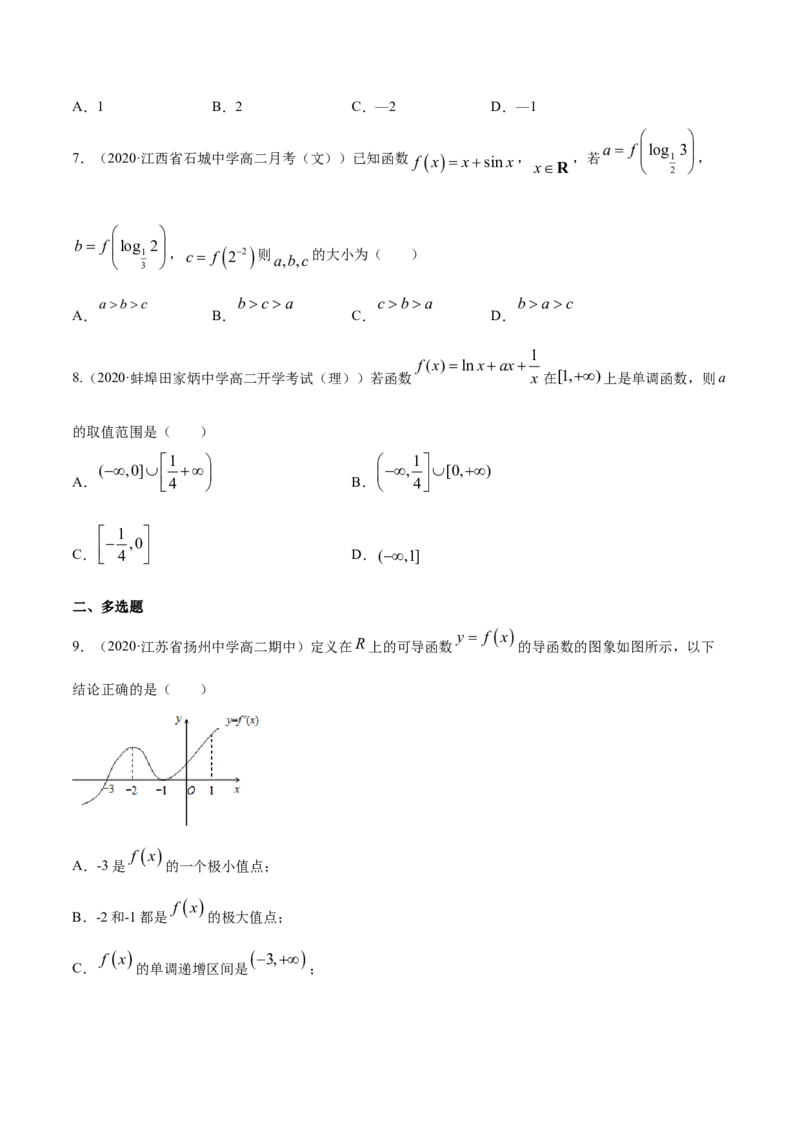y  f x 9．（2020·江苏省扬州中学高二期中）定义在R上的可导函数 的导函数的图象如图所示，以下 结论正确的是（ ） f x A．-3是 的一个极小值点； f x B．-2和-1都是 的极大值点； f x 3, C． 的单调递增区间是 ；f x ,3 D． 的单调递减区间是 ． 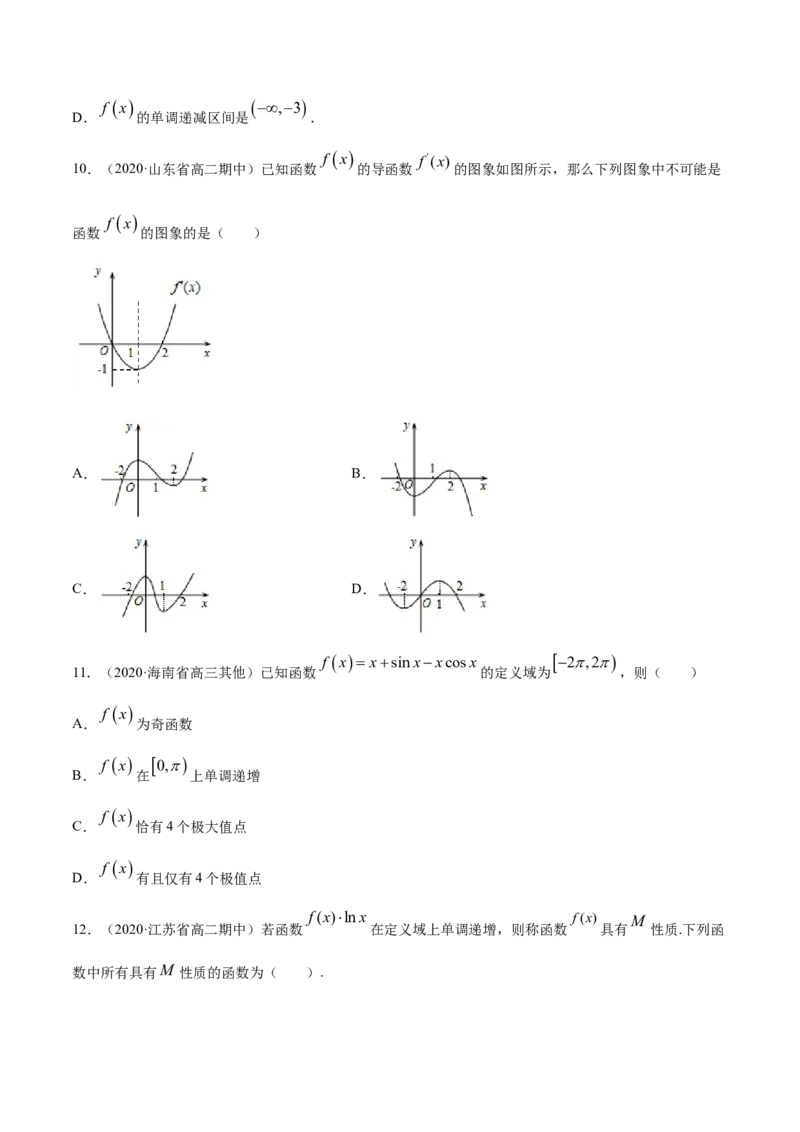f x f(x) 10．（2020·山东省高二期中）已知函数 的导函数 的图象如图所示，那么下列图象中不可能是 f x 函数 的图象的是（ ） A． B． C． D． f x xsinxxcosx 2,2 11．（2020·海南省高三其他）已知函数 的定义域为 ，则（ ） f x A． 为奇函数 f x 0, B． 在 上单调递增 f x C． 恰有4个极大值点 f x D． 有且仅有4个极值点 f(x)lnx f(x) M 12．（2020·江苏省高二期中）若函数 在定义域上单调递增，则称函数 具有 性质.下列函 数中所有具有M 性质的函数为（ ）.1 1 f(x) f(x) 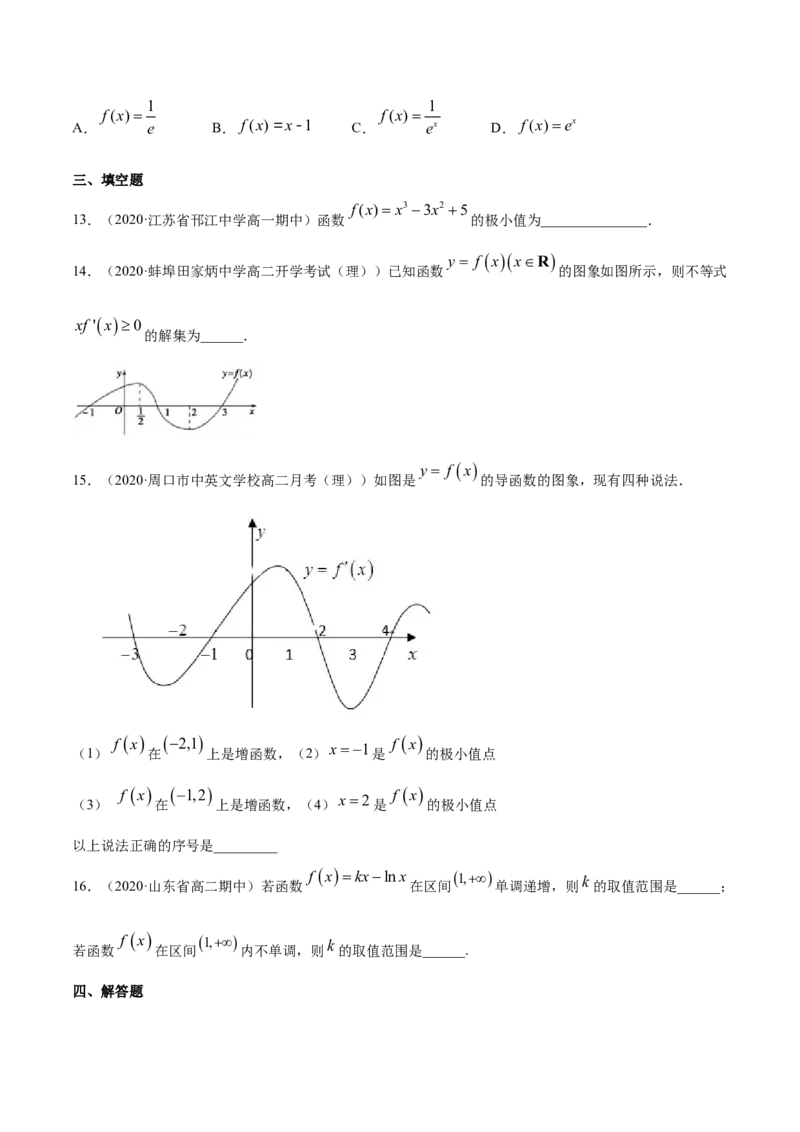A． e B． f(x)=x-1 C． ex D． f(x)ex 三、填空题 f(x) x33x2 5 13．（2020·江苏省邗江中学高一期中）函数 的极小值为_______________． y  f xxR 14．（2020·蚌埠田家炳中学高二开学考试（理））已知函数 的图象如图所示，则不等式 xf 'x0 的解集为______． y  f x 15．（2020·周口市中英文学校高二月考（理））如图是 的导函数的图象，现有四种说法． f x 2,1 f x x1 （1） 在 上是增函数，（2） 是 的极小值点 f x 1,2 f x x2 （3） 在 上是增函数，（4） 是 的极小值点 以上说法正确的序号是_________ f xkxlnx 1, k 16．（2020·山东省高二期中）若函数 在区间 单调递增，则 的取值范围是______； f x 1, k 若函数 在区间 内不单调，则 的取值范围是______. 四、解答题f(x) xex 17．（2020·横峰中学高二开学考试（文））已知函数 ． y  f(x) (1, f(1)) （1）求曲线 在点 处的切线方程； f(x) （2）求函数 的极值． f(x) x2 2(a1)x2alnx(a 0) 18．（2020·黄冈中学第五师分校高二期中（理））已知函数 . a1 y  f(x) (1, f(1)) （1）当 时，求曲线 在点 处的切线方程； f(x) （2）求 的单调区间； 1 f xax2 blnx 19．（2020·阳江市第三中学高二期中）已知函数 在x1处有极值2 ． （1）求a,b的值； f x （2）求 的单调区间． 2 x 20．（2020·山东省高二期中）已知函数 f(x)ax3 x2 bx在 3与x1时都取得极值. a b （1）求 ， 的值；  2 f  （2）求函数 f x 的单调区间，并指出   3  与 f 1 是极大值还是极小值. 21．（2020·江苏省扬州中学高二期中）已知函数f（x）＝ax3+bx2﹣3x在x＝﹣1和x＝3处取得极值. （1）求a，b的值 （2）求f（x）在[﹣4，4]内的最值. f x x2 8lnx 22．（2020·安徽省池州一中高二期中（文））已知函数 f x ; （1）求函数 的极值 1  ,e （2）求函数 f x 在区间  e  上的最值．