专题25一元函数的导数及其应用（单元测试卷）（原卷版）_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_高中数学新教材人教A版选择性必修配套提升训练(等10份资料)

专题25 《一元函数的导数及其应用》单元测试卷 一、单选题 f 1x f 1 1．（2020·夏津第一中学高二期中）设函数 f x x，则  l x i  m  x  （ ） A．0 B．1 C．2 D．－1 f(x) x32x2 x3 f(2) 2．（2019·辰溪县第一中学高二月考）已知函数 ，求 ( ) A．1 B．5 C．4 D．3 f x2xaex f '13e y  f x 3．（2020·黑山县黑山中学高二月考）已知函数 ，且 ，则曲线 在 x0处的切线方程为（ ） x y10 x y10 A． B． x3y10 x3y10 C． D． f x3xa2lnx 4．（2020·湖北省高二期中）若函数 不是单调函数，则实数a的取值范围是（ ）  1 , A．   2   B． 2, C． 0, D． ,2 5．（2020·湖南省高三一模（文））函数y=xlnx的图象大致是( ) A． B． C． D．f(x)2xf(e)lnx f e 6．（2020·四川省南充市白塔中学高二月考（理））已知函数 ，则 ( ) A．e B．e C．1 D．1 y  x3 3x4 7．（2020·夏津第一中学高二期中）函数 有（ ） A．极大值6，极小值2 B．极大值2，极小值6 C．极小值－1，极大值2 D．极小值2，极大值8 ln(x1)ax2,x0,  f(x) 1 8．（2020·福建省高三其他（文））若函数 x a,x0. 的最大值为 ，则实数   x f(1) a 的取值范围为（ ）  1 1   0,   ,  A．(,e] B． e C．e  D．[e,) 二、多选题 0,1 9．（2019·福建省莆田一中高二期末）（多选题）下列函数中，既是奇函数又在区间 上单调递增的是 （ ） y 2x34x y  xsinx y log x y 2x 2x A． B． C． 2 D． 1 10．（2020·江苏省高二期中）直线y xb能作为下列（ ）函数的图像的切线. 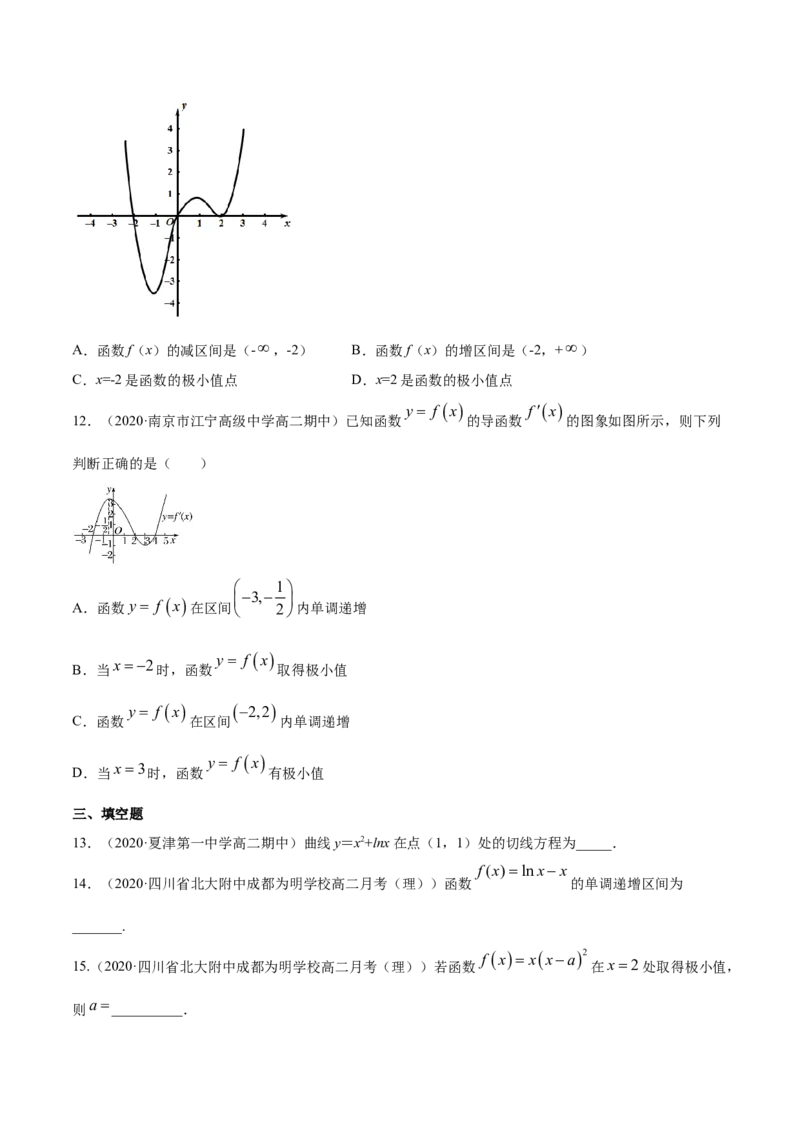2 1 f(x) A． x B． f(x) x4 C． f(x)sinx D． f(x)ex f x 11．（2020·山东省潍坊一中高二月考）已知函数f（x）的定义域为R且导函数为 ，如图是函数 y  xfx 的图像，则下列说法正确的有（ ）A．函数f（x）的减区间是（-，-2） B．函数f（x）的增区间是（-2，+） C．x=-2是函数的极小值点 D．x=2是函数的极小值点 y  f x f x 12．（2020·南京市江宁高级中学高二期中）已知函数 的导函数 的图象如图所示，则下列 判断正确的是（ ）  1 3, A．函数y  f x 在区间   2  内单调递增 y  f x x2 B．当 时，函数 取得极小值 y  f x 2,2 C．函数 在区间 内单调递增 y  f x x3 D．当 时，函数 有极小值 三、填空题 13．（2020·夏津第一中学高二期中）曲线y＝x2+lnx在点（1，1）处的切线方程为_____． f(x)lnxx 14．（2020·四川省北大附中成都为明学校高二月考（理））函数 的单调递增区间为 _______. f x xxa2 15.（2020·四川省北大附中成都为明学校高二月考（理））若函数 在x2处取得极小值， a 则 __________．1 f(x) xsinx,x[0,], 16．（2020·浙江省宁波诺丁汉附中高二期中）已知函数 2 则 f(x)的最小值为 ________，最大值为_______. 四、解答题 f(x)alnxx4 aR y  f x 17．（2018·营口市第二高级中学高二月考（文））设 ，（ ），曲线  1, f 1 y 在点 处的切线垂直于 轴. a （1）求 的值； y  f x （2）求函数 的单调区间. 1 18．（2020·福建省高二月考）已知函数 f xax2 blnx在 处有极值 . x1 2 a,b （1）求 的值； 1  ,2 （2）求函数 f x 在  2  上的最大值与最小值. 19．（2020·江西省新余一中高二月考（理））某同学大学毕业后，决定利用所学专业进行自主创业，经过 x C(x) 市场调查，生产一小型电子产品需投入固定成本2万元，每生产 万件，需另投入流动成本 万元，当 1 e3 C(x) x2 2x C(x)6xlnx 17 年产量小于7万件时， 3 （万元）；当年产量不小于7万件时， x （万元）.已知每件产品售价为6元，假若该同学生产的商品当年能全部售完. P(x) x （1）写出年利润 （万年）关于年产量 （万件）的函数解析式；（注：年利润=年销售收入-固定成 本-流动成本） （2）当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润是多少？ e3 20 （取 ）. C y  x33x2 2x 20．（2020·横峰中学高二开学考试（理））已知曲线 的方程是 ．x1 l （1）求曲线在 处的切线方程 1； l : y kx l C x ,y x 0 l （2）若 2 ，且直线 2与曲线 相切于点 0 0 0 ，求直线 2的方程及切点坐标． 1 f(x) x2 mlnx 21．（2020·天津大钟庄高中高二月考）已知函数 2 (mR) m2 （1）当 时， f x ①求函数 在x=1处的切线方程； f x [1,e] ②求函数 在 上的最大，最小值． 1  , （2）若函数 f x 在  2   上单调递增，求实数m的取值范围； f xlnxxm(mR) 22．（2020·黄冈中学第五师分校高二期中（理））已知函数 ． f x m （1）若函数 有两个零点，求 的取值范围； 1  ,1 （2）证明：当m3时，关于x的不等式 f xx2ex 0在  2  上恒成立．