专题24导数在研究函数中的应用（2）（原卷版）_E015高中全科试卷_数学试题_选修2_06.专项练习_专题24导数在研究函数中的应用（2）-高中数学新教材人教A版选择性必修配套提升训练

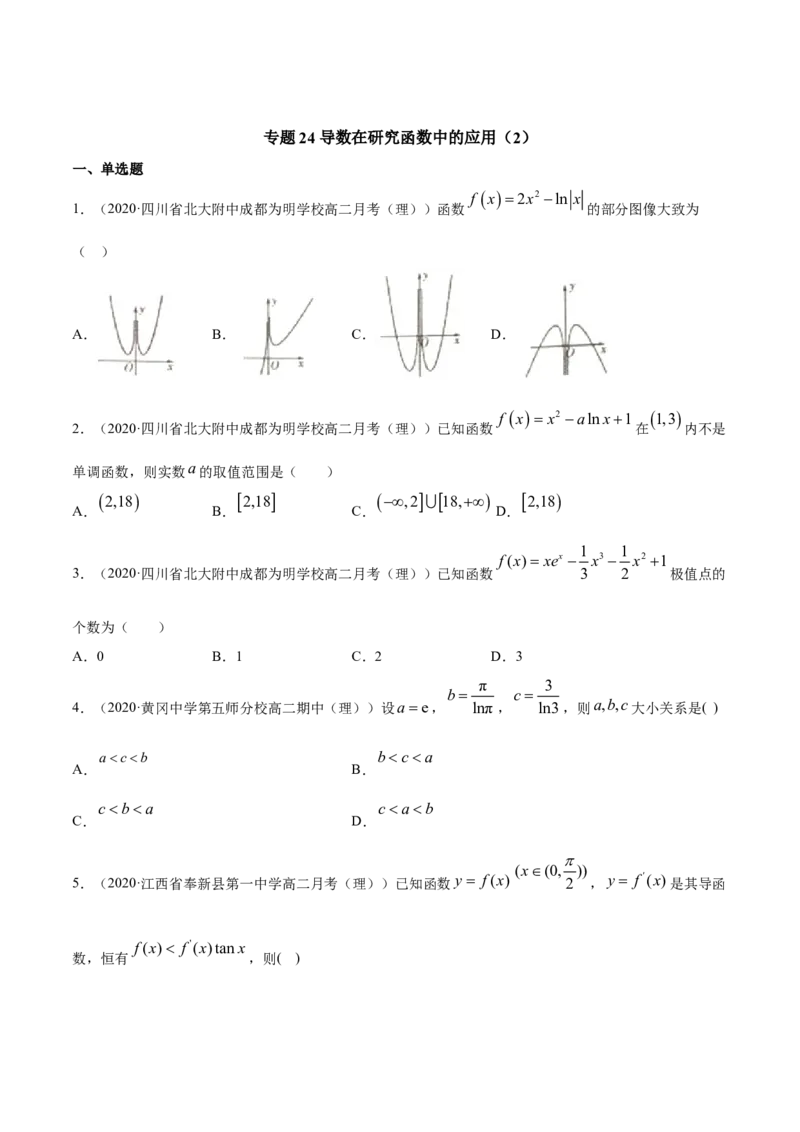
专题24 导数在研究函数中的应用（2） 一、单选题 f x2x2 ln x 1．（2020·四川省北大附中成都为明学校高二月考（理））函数 的部分图像大致为 （ ） A． B． C． D． f x x2 alnx1 1,3 2．（2020·四川省北大附中成都为明学校高二月考（理））已知函数 在 内不是 a 单调函数，则实数 的取值范围是（ ） 2,18 2,18 ,2 18, 2,18  A． B． C． D． 1 1 f(x) xex  x3 x2 1 3．（2020·四川省北大附中成都为明学校高二月考（理））已知函数 3 2 极值点的 个数为（ ） A．0 B．1 C．2 D．3 π 3 b c 4．（2020·黄冈中学第五师分校高二期中（理））设a e， lnπ ， ln3，则a,b,c大小关系是( ) acb bca A． B． cba cab C． D．  (x(0, )) 5．（2020·江西省奉新县第一中学高二月考（理））已知函数y  f(x) 2 ，y  f(x)是其导函 f(x) f '(x)tanx 数，恒有 ，则( )    3f( ) 2f( ) 3f( ) 2f( ) A． 4 3 B． 4 3    f(1)2f( )sin1 2f( ) f( ) C． 6 D． 6 4 0 x  x a 6．（2020·黄冈中学第五师分校高二期中（理））若对于任意的 1 2 ，都有 x lnx x lnx 2 1 1 2 1 x x ，则a的最大值为（ ） 1 2 1 A．2e B．e C．1 D．2 f x 0, 7．（2020·蚌埠田家炳中学高二开学考试（理））已知函数 的定义域为 ，且满足 f xxfx0 f x f x x1 f  x2 1   f x1 （ 是 的导函数），则不等式 的解集为 （ ） ,2 1, 1,2 1,2 A． B． C． D． ,00, f x 8．（2020·江西省石城中学高二月考（文））已知定义在 上的偶函数 的导函数为 f x 2f xxfx2 x2f x4f 2 x2 4 x ，对定义域内的任意 ，都有 成立，则使得 成立的 x 的取值范围为（ ）  x x0,2  2,0 0,2 A． B．  ,2 2, ,2 0,2   C． D． 二、多选题 a b1,e 9．（2020·山东省高二期中）已知 为自然对数的底数，则下列不等式一定成立的是（ ） aea beb alnbblna alna blnb bea aeb A． B． C． D．f xex asinx x, 10．（2020·江苏省扬州中学高二期中）关于函数 ， ，下列说法正确的是 （ ） f x  0, f 0 2x y10 A．当a1时， 在 处的切线方程为 f x 1 f x 0 B．当a1时， 存在唯一极小值点 x 0且 0 f x , a0 C．对任意 ， 在 上均存在零点 f x , D．存在a0， 在 上有且只有一个零点 f x xcosxsinx 11．（2020·山东省高二期中）已知函数 ，下列结论中正确的是（ ）  A．函数 f x在x 时，取得极小值 2 1 x0, f x0 B．对于 ， 恒成立 x sinx 1  1 C．若0 x  x ，则 x sinx 1 2 2 2 sinx   2 a  b x 0,   D．若 x ，对于  2恒成立，则a的最大值为，b的最小值为1 2 f x lnx 12．（2020·盐城市大丰区新丰中学高二期中）关于函数 x ，下列判断正确的是（ ） f x x2 A． 是 的极大值点 y=f ( x) - x B．函数 有且只有1个零点 f xkx k C．存在正实数 ，使得 成立 x x x  x f x  f x  x x 4 D．对任意两个正实数 1， 2，且 1 2，若 1 2 ，则 1 2 . 三、填空题 13．（2020·福建省南安市侨光中学高二月考）已知a为函数f(x)=x3-12x的极小值点,则a=____.a  eax 1  2  x 1 lnx   14．（2020·江苏省扬州中学高二期中）若对任意x＞0，恒有  x ，则实数a的取值 范围为_____. f(x)  exm ax  (lnxax) 15．（2020·宁夏回族自治区宁夏育才中学高二开学考试（理））设函数 ， a f(x)0 m 若存在实数 使得 恒成立，则 的取值范围是____________． 16．（2020·山东省实验中学高二期中）某商场销售某种商品，该商品的成本为3元/千克，每日的销售量 1 y  5(x6)2 y(单位：千克)与销售价格x(单位：元/千克)满足关系式 x3 ，其中3 x6，当销售价格 为_______元时，商场每日销售该商品所获得的最大利润为__________元. 四、解答题 f(x) x2 lnx 17．（2020·周口市中英文学校高二月考（理））已知函数 f(x) [1,e] （1）求函数 在 上的最大值和最小值； 2 1 g(x) x3  x2 （2）求证：当x(1,)时，函数 f(x)的图象在 3 2 的下方． f xex ax 18.（2020·广西壮族自治区高三其他（文））已知函数 ，其中e是自然对数的底数. a e f x0 （1）若 ，证明： ； x0, f x f x （2）若 时，都有 ，求实数a的取值范围. f(x)ex[x2 (2a5)x8a5](aR) 19．（2020·甘肃省高三二模（文））已知函数 ． a1 f(x) （1）当 时，求函数 的极值； x[0,2] f(x)2e2 a （2）当 时，若不等式 恒成立，求实数 的取值范围． f(x)aex bx 20．（2020·福建省高三二模（文））已知函数 ．a1 f(x) （1）当 时，求 的极值； 4 f(x)≥lnx （2）当a1时， 5 ，求整数b的最大值． （f x) 21．（2020·鸡泽县第一中学高二开学考试）已知函数 ae2x+(a﹣2) ex﹣x. f(x) （1）讨论 的单调性； f(x) （2）若 有两个零点，求a的取值范围. 22．（2020·湖南省高三一模（文））已知函数 f(x) ex 2(xlnx),a   x,ex ,b  (sinx,cosx),g(x)ab  x x0 f(x)0 （1）当 时，证明： ；   （2）当x[ , ]时，试判断 的零点个数. g(x) 2 2