专题29计数原理（单元测试卷）（原卷版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题29计数原理（单元测试卷）-高中数学新教材人教A版选择性必修配套提升训练

专题29 《计数原理》单元测试卷 一、单选题 5  1 1 1 1．（2020·四川省高三三模（理））  展开式中 项的系数为（ ）  x x3 10 5 A．10 B．5 C． D． (M x)5 M x2 2．（2020·横峰中学高二开学考试（理））二项式 （ 为常数）展开式中含 项的系数等于 10，则常数M （ ） A．2 B． C．-1 D．1 3．（2020·四川省高三三模（理））某中学高二学生会体育部共有5人，现需从体育部选派4人，分别担 任拔河比赛的裁判、记录结果、核查人数、维持纪律四项工作，每人只担任其中一项工作，其中甲没有担 任裁判工作，则不同的工作安排方式共有（ ） A．120种 B．48种 C．96种 D．60种 4．（2020·东营市第一中学高二期中）为做好社区新冠疫情防控工作，需将四名志愿者分配到甲、乙、丙 三个小区开展工作，每个小区至少分配一名志愿者，则不同的分配方案共有（ ）种 A．36 B．48 C．60 D．16 5．（2020·吉林省高三其他（理））树立劳动观念对人的健康成长至关重要，某实践小组共有4名男生，2 名女生，现从中选出4人参加校园植树活动，其中至少有一名女生的选法共有（ ） A．8种 B．9种 C．12种 D．14种 1.026 6．（2020·山东省高二期中） 的近似值（精确到0.01）为（ ） A．1.12 B．1.13 C．l.14 D．1.20 7．（2020·南昌市新建一中高二开学考试（理））已知 S C 2 1 7 C 2 2 7 C 2 3 7   C 2 2 7 7 ，则 S 除以9所得的 余数是 A．2 B．3 C．5 D．7 8．（2020·安徽省高三其他（理））北京2022年冬奥会和冬残奥会色彩系统的主色包括霞光红､迎春黄､天 霁蓝､长城灰､瑞雪白；间色包括天青､梅红､竹绿､冰蓝､吉柿；辅助色包括墨､金､银.若各赛事纪念品的色彩设计要求：主色至少一种､至多两种，间色两种､辅助色一种，则某个纪念品的色彩搭配中包含有瑞雪白､ 冰蓝､银色这三种颜色的概率为（ ） 8 2 1 2 A．225 B．45 C．15 D．15 二、多选题 ab11 9．（2020·山东省高二期中）关于 的说法，正确的是（ ） A．展开式中的二项式系数之和为2048 B．展开式中只有第6项的二项式系数最大 C．展开式中第6项和第7项的二项式系数最大 D．展开式中第6项的系数最大 10．（2020·江苏省扬州中学高二期中）将高二（1）班的四个同学分到语文、数学、英语三个兴趣小组， 每个兴趣小组至少有一名同学的分配方法有多少种？下列结论正确的有（ ） C1C1C1C1 C2A3 A． 3 2 1 3 B． 4 3 C1C2A2 C． 3 4 2 D．18 (2x1)10 a a xa x2  a x10,xR 11．（2020·江苏省高二期中）若 0 1 2  10 ，则（ ） a 1 a 0 A． 0 B． 0 a a a  a 310 a a a  a 3 C． 0 1 2  10 D． 0 1 2  10 6  1  2x 12．（2020·海南省高三其他）对于  x2   的展开式，下列说法正确的是（ ） A．展开式共有6项 B．展开式中的常数项是-240 C．展开式中各项系数之和为1 D．展开式中的二项式系数之和为64 三、填空题 13．（2020·四川省南充市白塔中学高二月考（理））安排3名志愿者完成4项工作，每人至少完成1项， 每项工作由1人完成，则不同的安排方式有_______.1 (2x2  )6 14．（2020·北京市鲁迅中学高二月考）二项式 x 的展开式中的常数项是_______.（用数字作答） 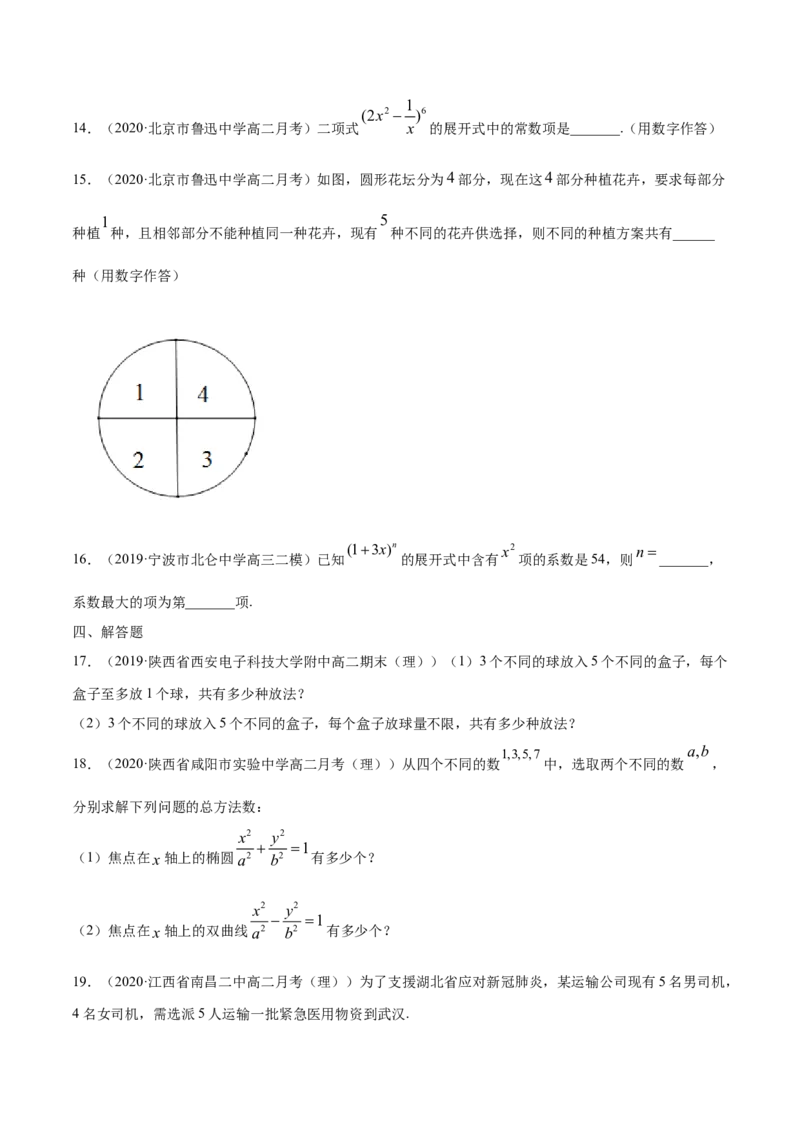15．（2020·北京市鲁迅中学高二月考）如图，圆形花坛分为4部分，现在这4部分种植花卉，要求每部分 1 5 种植 种，且相邻部分不能种植同一种花卉，现有 种不同的花卉供选择，则不同的种植方案共有______ 种（用数字作答） (13x)n x2 n 16．（2019·宁波市北仑中学高三二模）已知 的展开式中含有 项的系数是54，则 _______， 系数最大的项为第_______项. 四、解答题 17．（2019·陕西省西安电子科技大学附中高二期末（理））（1）3个不同的球放入5个不同的盒子，每个 盒子至多放1个球，共有多少种放法？ （2）3个不同的球放入5个不同的盒子，每个盒子放球量不限，共有多少种放法？ 1,3,5,7 a,b 18．（2020·陕西省咸阳市实验中学高二月考（理））从四个不同的数 中，选取两个不同的数 ， 分别求解下列问题的总方法数： x2 y2  1 （1）焦点在x轴上的椭圆a2 b2 有多少个？ x2 y2  1 （2）焦点在x轴上的双曲线a2 b2 有多少个？ 19．（2020·江西省南昌二中高二月考（理））为了支援湖北省应对新冠肺炎，某运输公司现有5名男司机， 4名女司机，需选派5人运输一批紧急医用物资到武汉.（1）如果派3名男司机、2名女司机，共有多少种不同的选派方法？ （2）至少有两名男司机，共有多少种不同的选派方法？ 20. （2020·江苏省邗江中学高二期中）有3名男生、4名女生，在下列不同条件下，求不同的排列方法总数. （1）选5人排成一排； （2）排成前后两排，前排4人，后排3人； （3）全体排成一排，甲不站排头也不站排尾； （4）全体排成一排，女生必须站在一起； （5）全体排成一排，男生互不相邻. n  1  2x 21．（2020·福建省南平市高级中学高二期中）已知  展开式前三项的二项式系数和为22.  x  （1）求展开式中的常数项； （2）求展开式中二项式系数最大的项. 22．（2020·扬州大学附属中学高二月考）已知8件不同的产品中有3件次品，现对它们一一进行测试，直 至找到所有次品． (1)若恰在第2次测试时，找到第一件次品，第6次测试时，才找到最后一件次品，则共有多少种不同的测 试方法？ (2)若至多测试5次就能找到所有次品，则共有多少种不同的测试方法？