文档内容
2.4.2 圆的一般方程(同步练习)
一、选择题
1.(多选)若a∈,方程x2+y2+2ax+2ay+2a2+a-1=0表示圆,则a的值可以
为( )
A.-2 B.0 C.1 D.
2.与圆C:x2+y2-2x+4y-1=0有相同圆心,且半径是圆C的半径的一半的圆
的方程为( )
A.x2+y2-2x+4y+2=0 B.x2+y2-2x+4y+1=0
C.x2+y2-2x+4y-=0 D.x2+y2-2x+4y+=0
3.圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为,则a=( )
A.0或-1 B.0 C.7 D.-1或7
4.如果圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)关于直线y=x对称,则有(
)
A.D+E=0 B.D=E C.D=F D.E=F
5.已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所
包围的图形的面积等于( )
A.π B.4π C.8π D.9π
6.已知圆x2+y2-2mx-(4m+2)y+4m2+4m+1=0(m≠0)的圆心在直线x+y-
7=0上,则该圆的面积为( )
A.4π B.2π C.π D.
7.已知圆C:x2+y2=4,则圆C关于直线l:x-y-3=0对称的圆的方程为(
)
A.x2+y2-6x+6y+14=0 B.x2+y2+6x-6y+14=0
C.x2+y2-4x+4y+4=0 D.x2+y2+4x-4y+4=0
二、填空题
8.如果x2+y2-2x+y+k=0是圆的方程,则实数k的取值范围是________
9.若直线 x+y+a=0 平分圆 x2+y2-2x+4y+1=0 的面积,则实数 a=
________
10.已知点 A(1,2)在圆 x2+y2+2x+3y+m=0 外部,则实数 m 的取值范围是
________
11.圆x2+y2+4x-6y+a=0关于直线y=x+b成轴对称图形,则a-b的取值范
围是________12.如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆的面积最大时,圆心坐标
为________
三、解答题
13.已知圆C:x2+y2+Dx+Ey+3=0,圆心在直线x+y-1=0上,且圆心在第
二象限,半径为,求圆的一般方程.
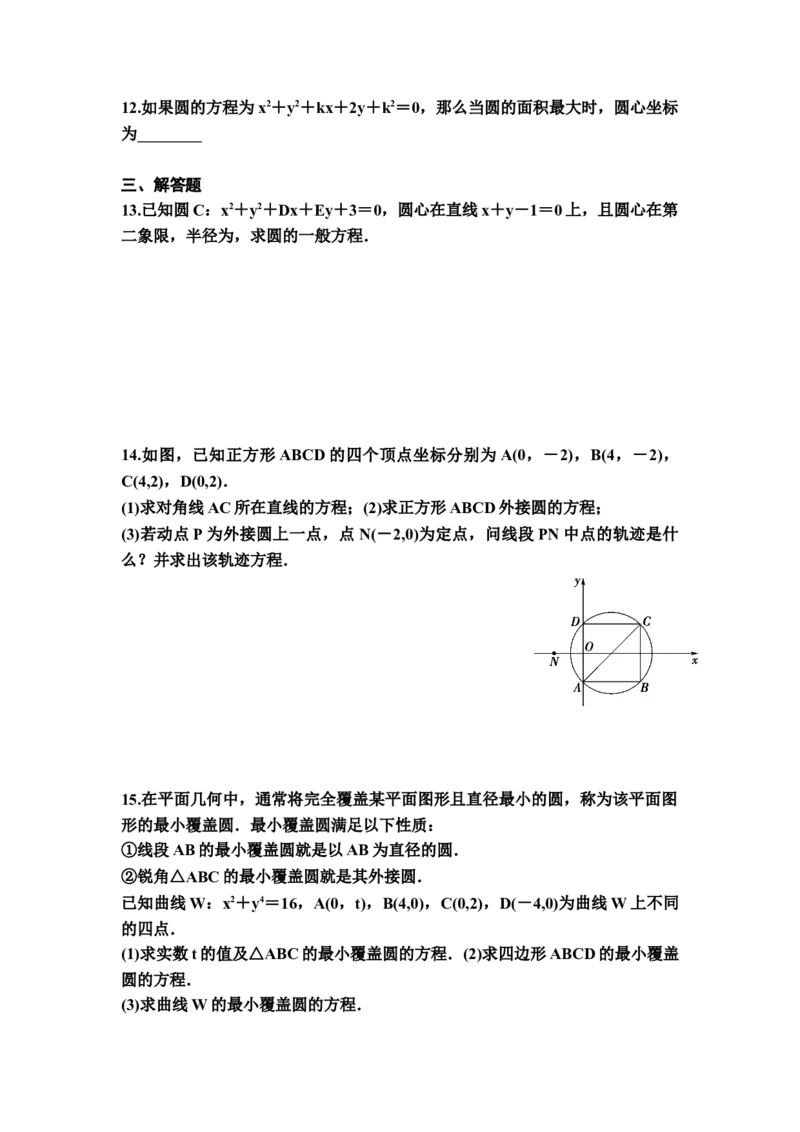
14.如图,已知正方形ABCD的四个顶点坐标分别为A(0,-2),B(4,-2),
C(4,2),D(0,2).
(1)求对角线AC所在直线的方程;(2)求正方形ABCD外接圆的方程;
(3)若动点P为外接圆上一点,点 N(-2,0)为定点,问线段 PN中点的轨迹是什
么?并求出该轨迹方程.
15.在平面几何中,通常将完全覆盖某平面图形且直径最小的圆,称为该平面图
形的最小覆盖圆.最小覆盖圆满足以下性质:
①线段AB的最小覆盖圆就是以AB为直径的圆.
②锐角△ABC的最小覆盖圆就是其外接圆.
已知曲线W:x2+y4=16,A(0,t),B(4,0),C(0,2),D(-4,0)为曲线W上不同
的四点.
(1)求实数t的值及△ABC的最小覆盖圆的方程.(2)求四边形ABCD的最小覆盖
圆的方程.
(3)求曲线W的最小覆盖圆的方程.参考答案:
一、选择题
1.ABD 2.D 3.D 4.B 5.B 6.A 7.A
二、填空题
8.答案: 9.答案:1 10.答案: 11.答案:(-∞,8) 12.答案:(0,-1)
三、解答题
13.解:圆心C,因为圆心在直线x+y-1=0上,所以---1=0,即D+E=-2,①
又r==,所以D2+E2=20,②
由①②可得或
又圆心在第二象限,所以-<0,即D>0,所以所以圆的一般方程为x2+y2+2x-4y+3=0.
14.解:(1)由两点式可知,对角线AC所在直线的方程为=,整理得x-y-2=0.
(2)设G为外接圆的圆心,则G为AC的中点,∴G,即(2,0),
设r为外接圆的半径,则r=|AC|,则|AC|==4,∴r=2.
∴外接圆方程为(x-2)2+y2=8.
(3)设点P坐标为(x ,y),线段PN中点M坐标为(x,y),则x=,y=,∴x =2x+2,y =
0 0 0 0
2y,①
∵点P为外接圆上一点,∴(x-2)2+y=8,
0
将①代入并整理,得x2+y2=2,∴该轨迹是以原点为圆心,为半径的圆,轨迹方程为x2+
y2=2.
15.解:(1)由题意,得t=-2,由于△ABC为锐角三角形,其外接圆就是△ABC的最小覆盖
圆.
设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,则解得
所以△ABC的最小覆盖圆的方程为x2+y2-3x-4=0.
(2)因为线段DB的最小覆盖圆就是以DB为直径的圆,所以线段DB的最小覆盖圆的方程为
x2+y2=16.
又因为|OA|=|OC|=2<4(O为坐标原点),所以点A,C都在圆内.
所以四边形ABCD的最小覆盖圆的方程为x2+y2=16.
(3)由题意知曲线W为中心对称图形.设P(x,y),则x+y=16.所以|OP|2=x+y(O为坐标原点),且-2≤y≤2.
0 0 0
故|OP|2=x+y=16-y+y=-+,
所以当y=时,|OP| =,所以曲线W的最小覆盖圆的方程为x2+y2=.
max