文档内容
第八章 立体几何初步 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共40分)
1、(4分)若圆台的上、下底面面积分别为4,16,则圆台的中截面的面积为( ).
A.10 B.8 C.9 D.
2、(4分)已知正三棱锥 的六条棱长均为6,S是 及其内部的点构成的集合,设集合
,则T表示的区域的面积为( )
A. B.π C. D.
3、(4分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体
积为( )
A.π B. C. D.
4、(4分)已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C.2 D.
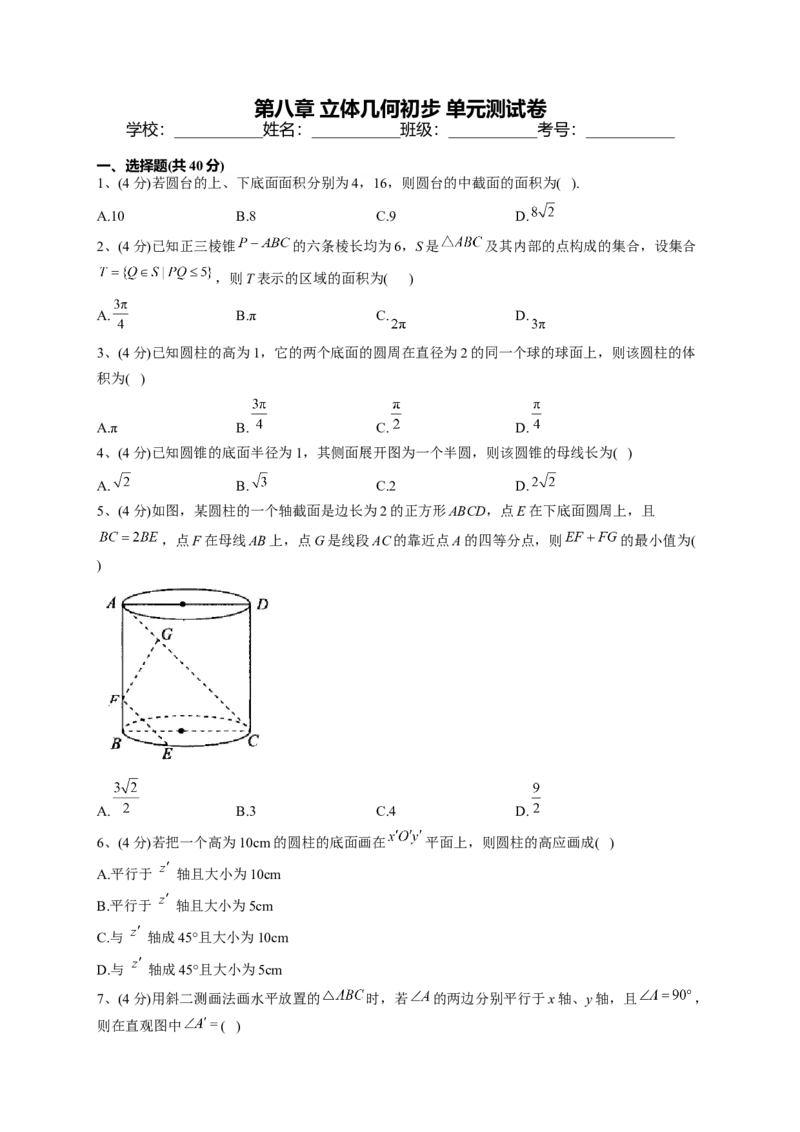
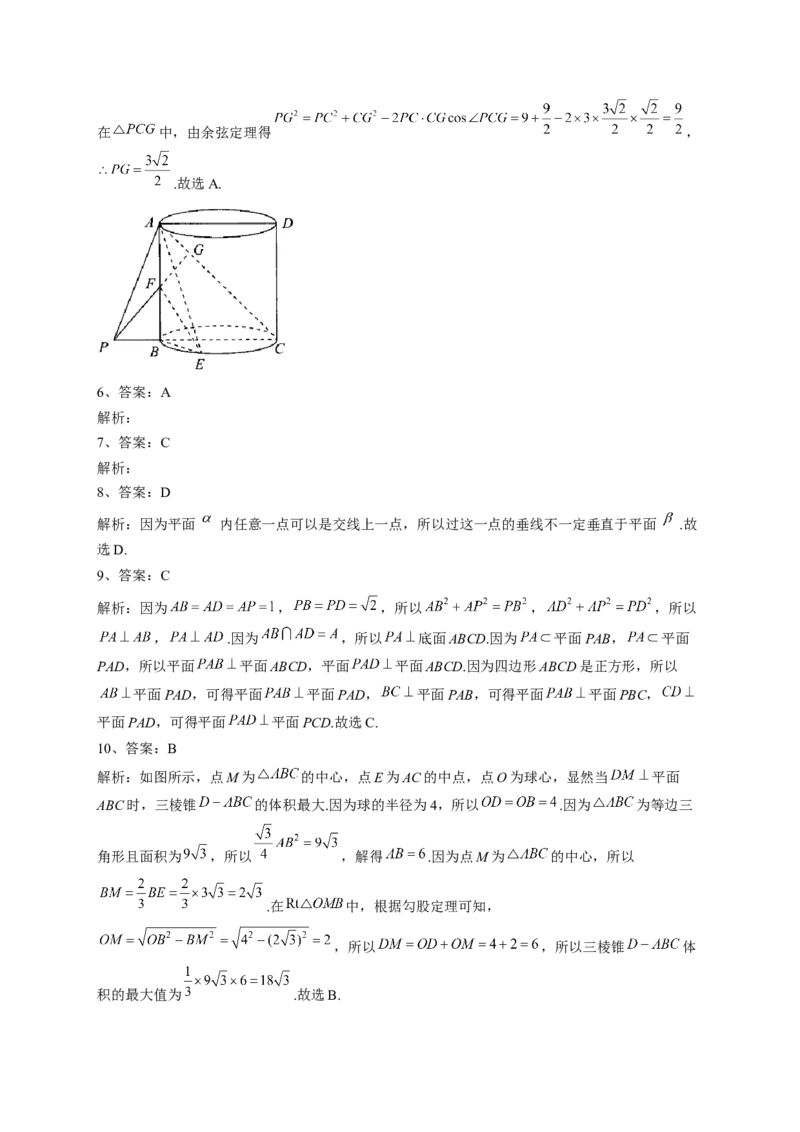
5、(4分)如图,某圆柱的一个轴截面是边长为2的正方形ABCD,点E在下底面圆周上,且
,点F在母线AB上,点G是线段AC的靠近点A的四等分点,则 的最小值为(
)
A. B.3 C.4 D.
6、(4分)若把一个高为10cm的圆柱的底面画在 平面上,则圆柱的高应画成( )
A.平行于 轴且大小为10cm
B.平行于 轴且大小为5cm
C.与 轴成45°且大小为10cm
D.与 轴成45°且大小为5cm
7、(4分)用斜二测画法画水平放置的 时,若 的两边分别平行于x轴、y轴,且 ,
则在直观图中 ( )A.45° B.135° C.45°或135° D.90°
8、(4分)下列命题中假命题是( )
A.如果平面 平面 ,平面 平面 , ,那么
B.如果平面 平面 ,那么平面 内一定存在直线平行于平面
C.如果平面 不垂直于平面 ,那么平面 内一定不存在直线垂直于平面
D.如果平面 平面 ,过 内任意一点作交线的垂线,那么此垂线必垂直于
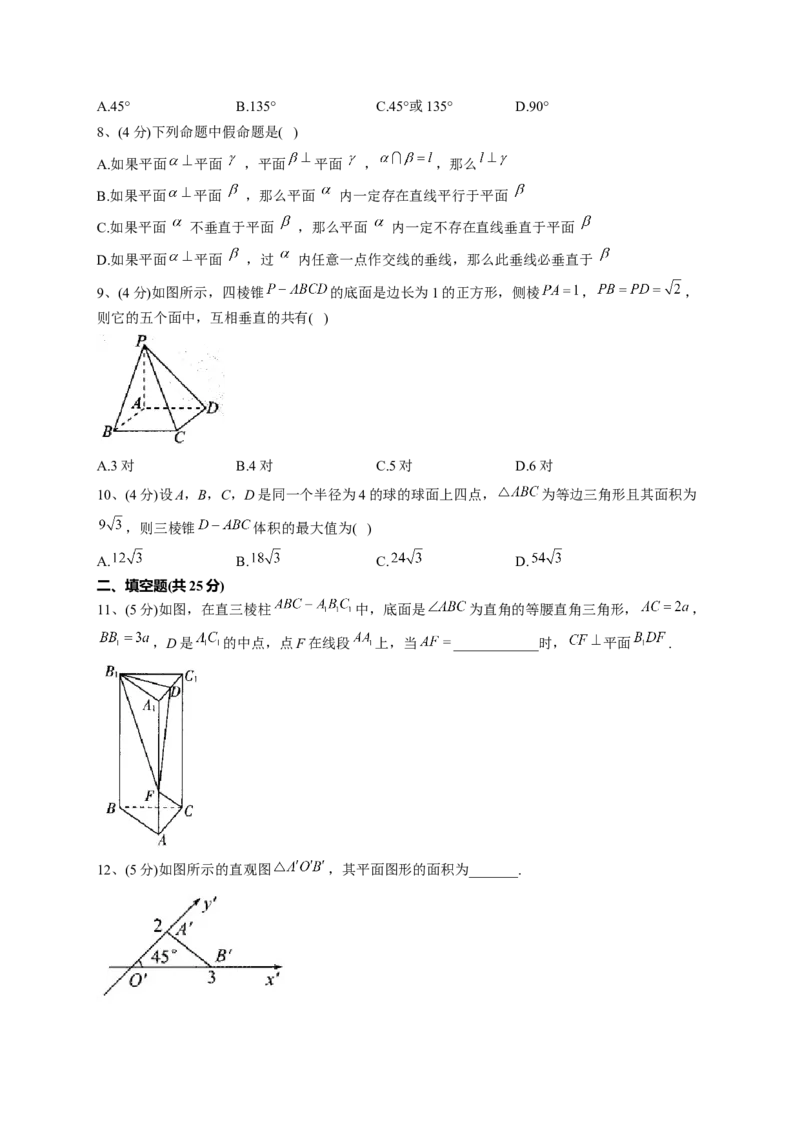
9、(4分)如图所示,四棱锥 的底面是边长为1的正方形,侧棱 , ,
则它的五个面中,互相垂直的共有( )
A.3对 B.4对 C.5对 D.6对
10、(4分)设A,B,C,D是同一个半径为4的球的球面上四点, 为等边三角形且其面积为
,则三棱锥 体积的最大值为( )
A. B. C. D.
二、填空题(共25分)
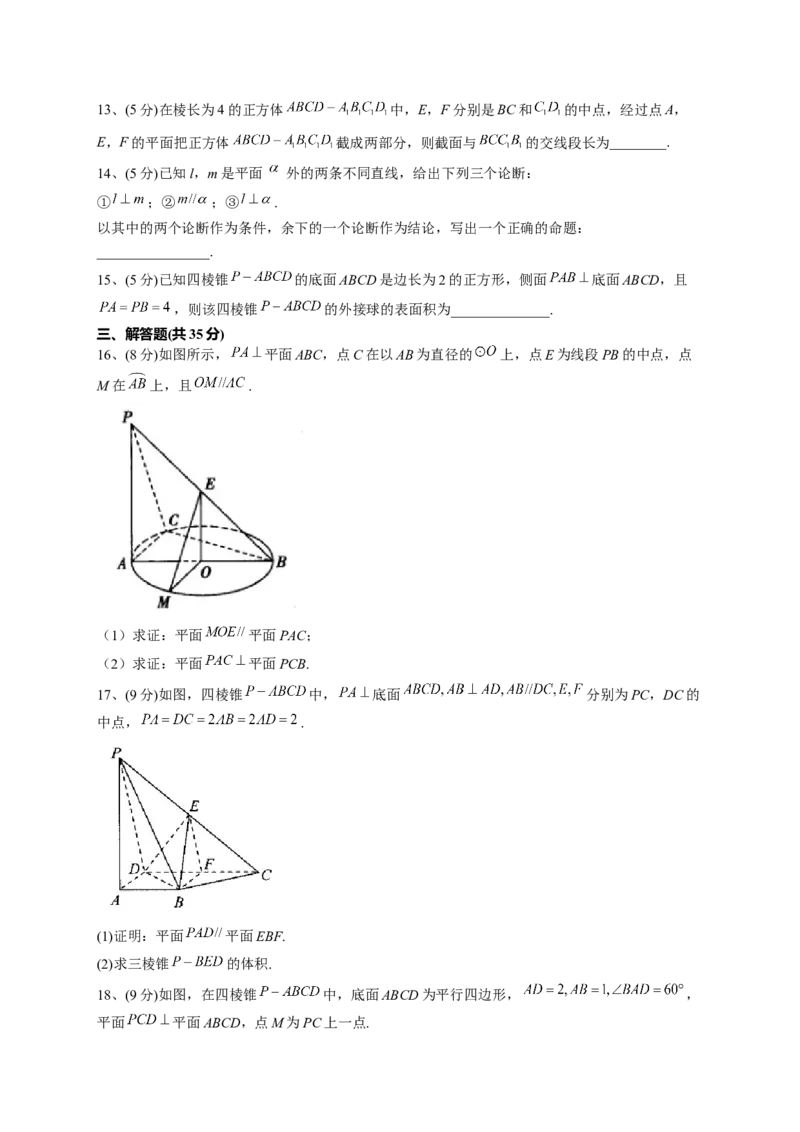
11、(5分)如图,在直三棱柱 中,底面是 为直角的等腰直角三角形, ,
,D是 的中点,点F在线段 上,当 ____________时, 平面 .
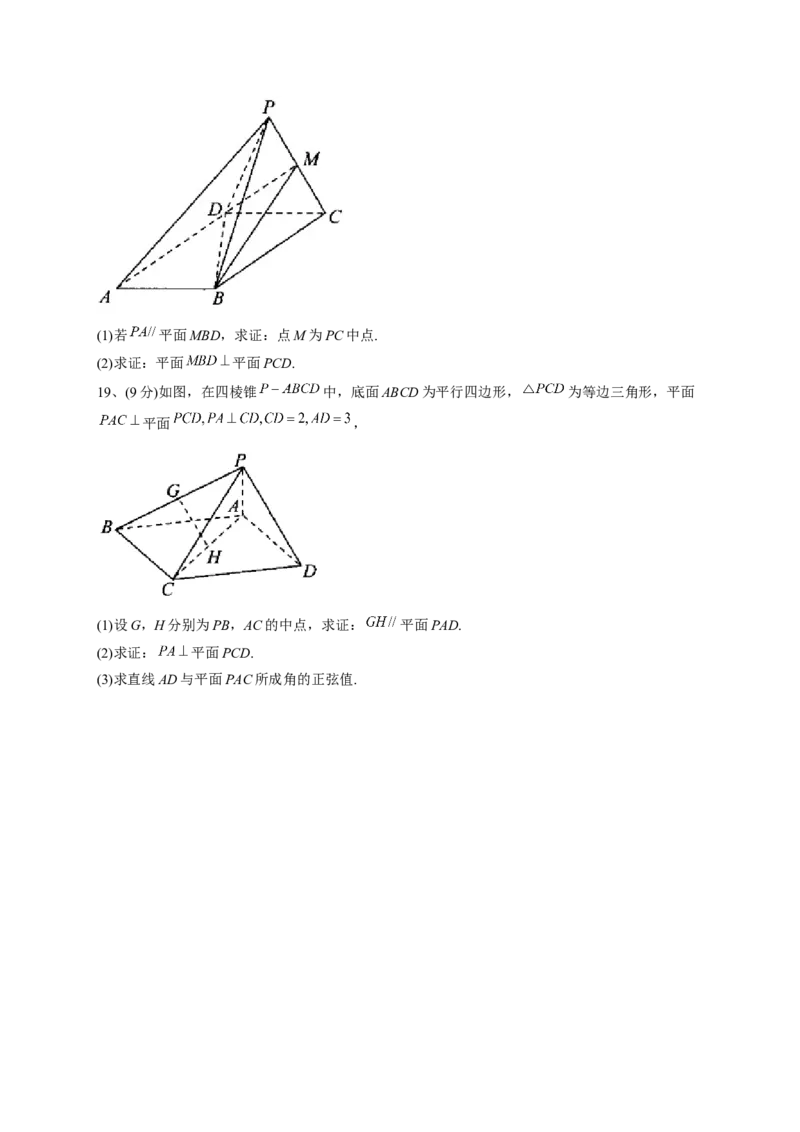
12、(5分)如图所示的直观图 ,其平面图形的面积为_______.13、(5分)在棱长为4的正方体 中,E,F分别是BC和 的中点,经过点A,
E,F的平面把正方体 截成两部分,则截面与 的交线段长为________.
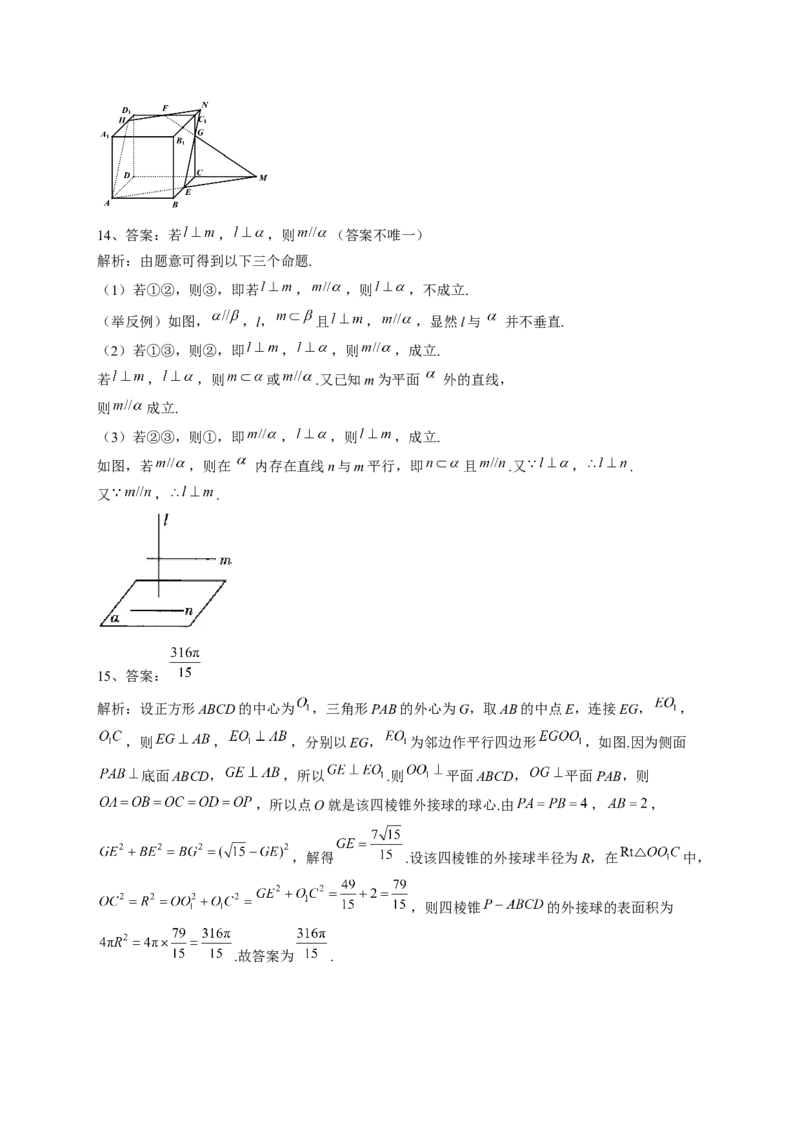
14、(5分)已知l,m是平面 外的两条不同直线,给出下列三个论断:
① ;② ;③ .
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
________________.
15、(5分)已知四棱锥 的底面ABCD是边长为2的正方形,侧面 底面ABCD,且
,则该四棱锥 的外接球的表面积为______________.
三、解答题(共35分)
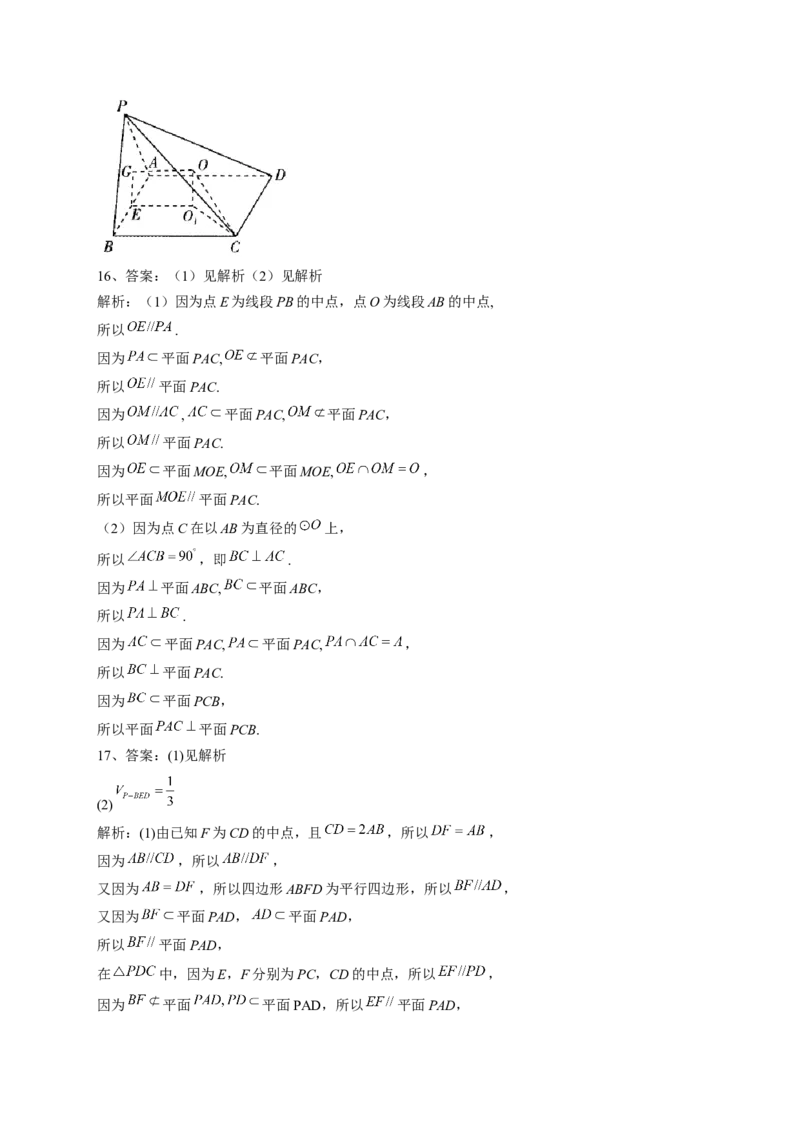
16、(8分)如图所示, 平面ABC,点C在以AB为直径的 上,点E为线段PB的中点,点
M在 上,且 .
(1)求证:平面 平面PAC;
(2)求证:平面 平面PCB.
17、(9分)如图,四棱锥 中, 底面 分别为PC,DC的
中点, .
(1)证明:平面 平面EBF.
(2)求三棱锥 的体积.
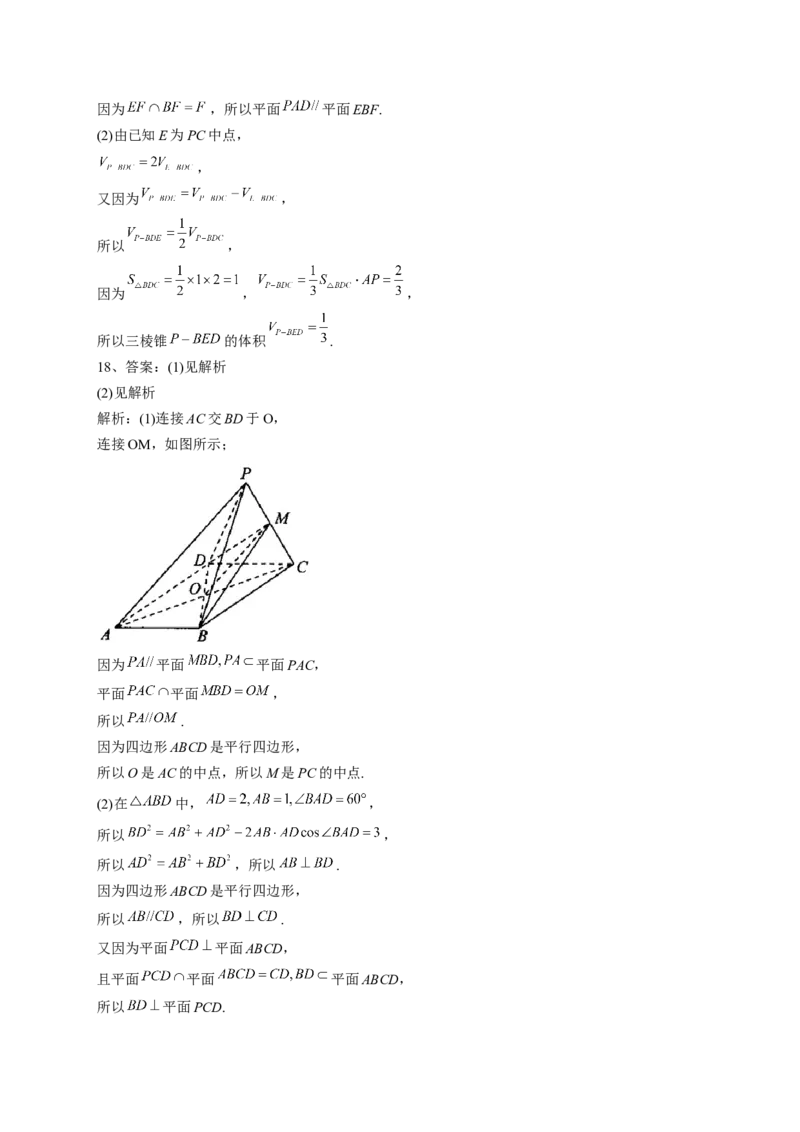
18、(9分)如图,在四棱锥 中,底面ABCD为平行四边形, ,
平面 平面ABCD,点M为PC上一点.(1)若 平面MBD,求证:点M为PC中点.
(2)求证:平面 平面PCD.
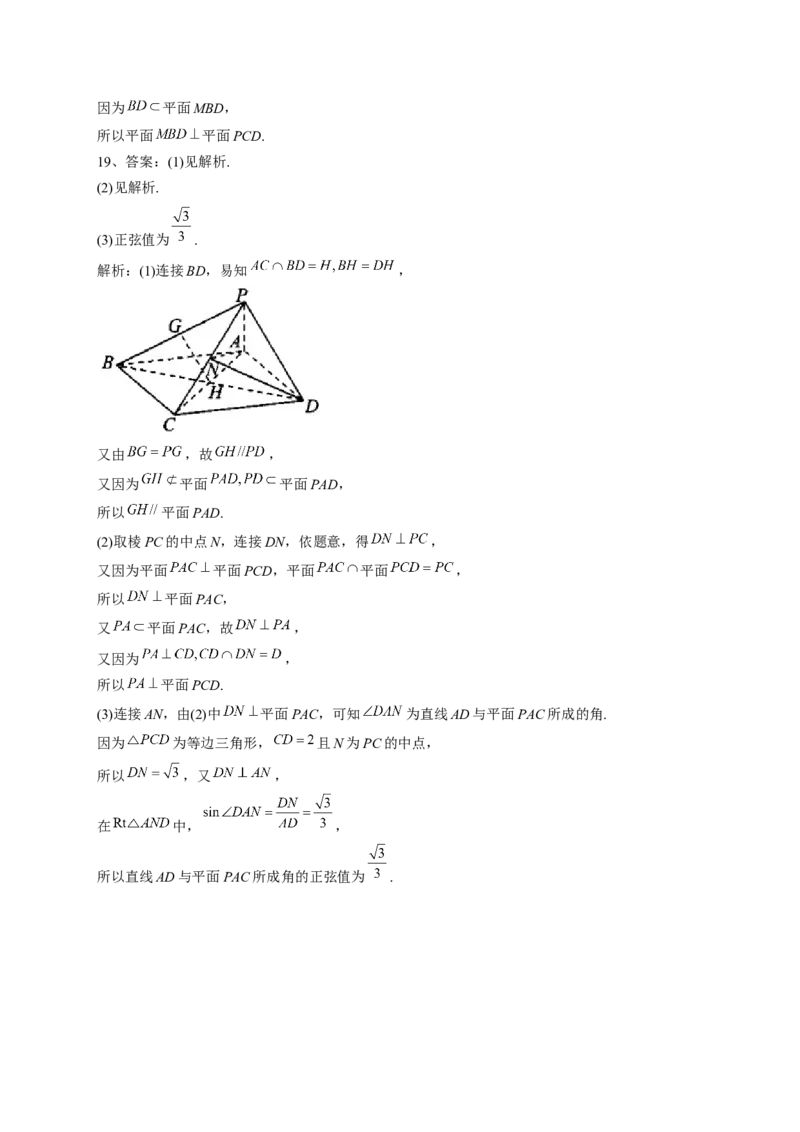
19、(9分)如图,在四棱锥 中,底面ABCD为平行四边形, 为等边三角形,平面
平面 ,
(1)设G,H分别为PB,AC的中点,求证: 平面PAD.
(2)求证: 平面PCD.
(3)求直线AD与平面PAC所成角的正弦值.参考答案
1、答案:C
解析:设圆台的上、下底面半径分别为 、 ,圆台中截面的半径为 ,则 ,
,解得 , ,所以 ,所以 .
2、答案:B
解析:设O为 的中心,连接PO,AO,在正三角形ABC中, ,在
中, ,当 时,连接OQ,根据勾股定理可得
,易知Q的轨迹是以O为圆心,半径为1的圆,由于集合 ,
故集合T表示的区每的面积为π,故选B.
3、答案:B
解析:由圆柱的两个底面的圆周在直径为2的同一个球的球面上,知球的直径为2,因此球的半径
.因为圆柱的高 ,所以圆柱的底面半径为 .由圆柱体的
体积公式得 .故选B.
4、答案:C
解析:依题意可知,半圆的弧长为 ,圆心角的弧度数为 ,由弧长公式可得该圆锥的母
线长为 .
5、答案:A
解析:如图,将 绕AB旋转到 的位置,并且点P在CB的延长线上,连接PG,交AB
于点F,此时 最小.
由已知可知轴截面ABCD是边长为2的正方形,所以 .在 中,由余弦定理得 ,
.故选A.
6、答案:A
解析:
7、答案:C
解析:
8、答案:D
解析:因为平面 内任意一点可以是交线上一点,所以过这一点的垂线不一定垂直于平面 .故
选D.
9、答案:C
解析:因为 , ,所以 , ,所以
, .因为 ,所以 底面ABCD.因为 平面PAB, 平面
PAD,所以平面 平面ABCD,平面 平面ABCD.因为四边形ABCD是正方形,所以
平面PAD,可得平面 平面PAD, 平面PAB,可得平面 平面PBC,
平面PAD,可得平面 平面PCD.故选C.
10、答案:B
解析:如图所示,点M为 的中心,点E为AC的中点,点O为球心,显然当 平面
ABC时,三棱锥 的体积最大.因为球的半径为4,所以 .因为 为等边三
角形且面积为 ,所以 ,解得 .因为点M为 的中心,所以
.在 中,根据勾股定理可知,
,所以 ,所以三棱锥 体
积的最大值为 .故选B.11、答案:a或2a
解析:由已知得 是等腰直角三角形, ,D是 的中点, . 平面
平面 ,平面 平面 , 平面 .又 平面
, .若 平面 ,则 .设 ,则 ,
, , ,解得 或2a.
12、答案:6
解析:由直观图可知其对应的平面图形AOB中, ,
所以 .
13、答案:
解析:如图,连接AE并延长交DC延长线于M,连接FM交 于G,连接EG并延长交 延长
线于N,连接NF并延长交 于H,连接AH,则五边形AEGFH为经过点A,E,F的正方体的截
面,因为E为BC的中点,所以 ,因为 ,所以 ,所以
,所以 ,因为 ,所以 ,所以 ,
所以 ,所以 ,所以截面与 的交线段长为
,故答案为: .14、答案:若 , ,则 (答案不唯一)
解析:由题意可得到以下三个命题.
(1)若①②,则③,即若 , ,则 ,不成立.
(举反例)如图, ,l, 且 , ,显然l与 并不垂直.
(2)若①③,则②,即 , ,则 ,成立.
若 , ,则 或 .又已知m为平面 外的直线,
则 成立.
(3)若②③,则①,即 , ,则 ,成立.
如图,若 ,则在 内存在直线n与m平行,即 且 .又 , .
又 , .
15、答案:
解析:设正方形ABCD的中心为 ,三角形PAB的外心为G,取AB的中点E,连接EG, ,
,则 , ,分别以EG, 为邻边作平行四边形 ,如图.因为侧面
底面ABCD, ,所以 .则 平面ABCD, 平面PAB,则
,所以点O就是该四棱锥外接球的球心.由 , ,
,解得 .设该四棱锥的外接球半径为R,在 中,
,则四棱锥 的外接球的表面积为
.故答案为 .16、答案:(1)见解析(2)见解析
解析:(1)因为点E为线段PB的中点,点O为线段AB的中点,
所以 .
因为 平面PAC, 平面PAC,
所以 平面PAC.
因为 , 平面PAC, 平面PAC,
所以 平面PAC.
因为 平面MOE, 平面MOE, ,
所以平面 平面PAC.
(2)因为点C在以AB为直径的 上,
所以 ,即 .
因为 平面ABC, 平面ABC,
所以 .
因为 平面PAC, 平面PAC, ,
所以 平面PAC.
因为 平面PCB,
所以平面 平面PCB.
17、答案:(1)见解析
(2)
解析:(1)由已知F为CD的中点,且 ,所以 ,
因为 ,所以 ,
又因为 ,所以四边形ABFD为平行四边形,所以 ,
又因为 平面PAD, 平面PAD,
所以 平面PAD,
在 中,因为E,F分别为PC,CD的中点,所以 ,
因为 平面 平面PAD,所以 平面PAD,因为 ,所以平面 平面EBF.
(2)由已知E为PC中点,
,
又因为 ,
所以 ,
因为 , ,
所以三棱锥 的体积 .
18、答案:(1)见解析
(2)见解析
解析:(1)连接AC交BD于O,
连接OM,如图所示;
因为 平面 平面PAC,
平面 平面 ,
所以 .
因为四边形ABCD是平行四边形,
所以O是AC的中点,所以M是PC的中点.
(2)在 中, ,
所以 ,
所以 ,所以 .
因为四边形ABCD是平行四边形,
所以 ,所以 .
又因为平面 平面ABCD,
且平面 平面 平面ABCD,
所以 平面PCD.因为 平面MBD,
所以平面 平面PCD.
19、答案:(1)见解析.
(2)见解析.
(3)正弦值为 .
解析:(1)连接BD,易知 ,
又由 ,故 ,
又因为 平面 平面PAD,
所以 平面PAD.
(2)取棱PC的中点N,连接DN,依题意,得 ,
又因为平面 平面PCD,平面 平面 ,
所以 平面PAC,
又 平面PAC,故 ,
又因为 ,
所以 平面PCD.
(3)连接AN,由(2)中 平面PAC,可知 为直线AD与平面PAC所成的角.
因为 为等边三角形, 且N为PC的中点,
所以 ,又 ,
在 中, ,
所以直线AD与平面PAC所成角的正弦值为 .