原创（新教材）下学期高二期末备考金卷数学教师版_E015高中全科试卷_数学试题_选修3_04.期末试卷_3.期末备考金卷

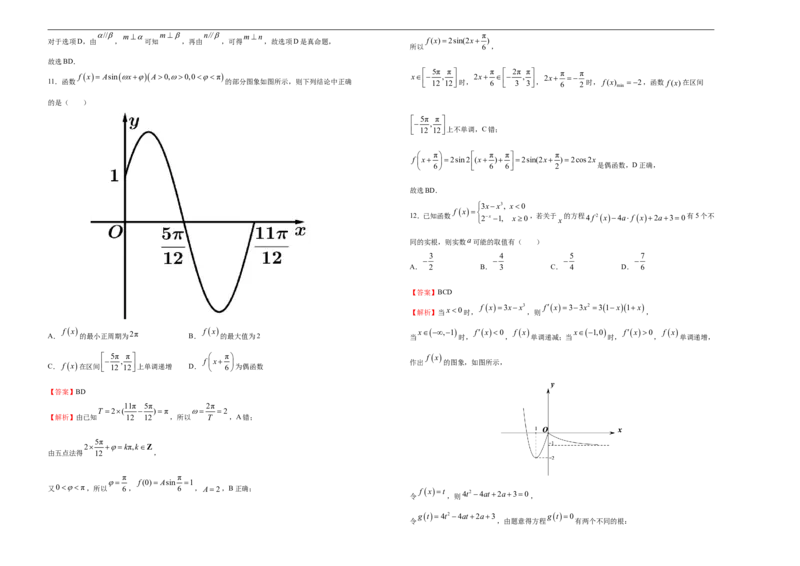
3．为达成“碳达峰､碳中和”的目标，我们需坚持绿色低碳可持续发展道路，可再生能源将会有一个 （新教材）下学期高二期末备考金卷 快速发展的阶段．太阳能是一种可再生能源，光伏是太阳能光伏发电系统的简称，主要有分布式与集 数 学 中式两种方式．下面的图表是近年来中国光伏市场发展情况表，则下列结论中正确的是（ ） 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴 在答题卡上的指定位置。 2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在 试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和 答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。 第Ⅰ卷（选择题） 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．已知集合 A  x ax1,aR  ， B1,1 ，若A B，则所有a的取值构成的集合为（ ） 1 1,1 0,1 1,0,1 A． B． C． D． 【答案】D 【解析】a0时，A满足题意； A．2013~2020年，年光伏新增装机规模同比(与上年相比)增幅逐年递减 1 1 1 x 1 1 B．2013~2020年，年光伏发电量与年份成负相关 a0时，ax1，得 a ，所以a 或a ，a1或a1， C．2013~2020年，年新增装机规模中，分布式的平均值大于集中式的平均值 {1,0,1} D．2013~2020年，每年光伏发电量占全国发电总量的比重与年份成正相关 所求集合为 ，故选D． 【答案】D z 1  【解析】A，2013~2020年，年光伏新增装机规模同比(与上年相比)增幅逐年递减， 2．设复数z 、z 在复平面内对应的点关于实轴对称，若z 2i，则 z （ ） 1 2 1 2 前几年递增，后面递减，故A错误； 3 4 3 4 3 4 3 4 B，2013~2020年，年光伏发电量与年份成正相关，故B错误；  i  i   i   i A．5 5 B．5 5 C． 5 5 D． 5 5 C，由图表可以看出，每一年装机规模，集中式都比分布式大， 因此分布式的平均值小于集中式的平均值，故C错误； 【答案】A D，根据图表可知，2013~2020年，每年光伏发电量占全国发电总量的比重随年份逐年增加， z 2i 2i2 34i 3 4 1      i 故每年光伏发电量占全国发电总量的比重与年份成正相关，故D正确， 【解析】由题意可得 ，因此， ， z 2i z 2i 2i2i 5 5 5 2 2 故选D． 故选A． 封封密密不不订订装装只只卷卷此此 号号位位座座 号号场场考考 号号证证考考准准 名名姓姓 级级班班△ABC A,B,C a b c acosB 3bsin Aa B S  2S  S S 2a a a a a a a a 4． 的内角 的对边分别为 ， ， ，已知 ，则 （ ） 【解析】由 n 是等差数列，可得 2 1 3，即 1 2 1 1 2 3， 2 3， π π π 2π a q  3 1 A．6 B．3 C．2 D． 3 设等比数列 a n  的公比为q， a n  是各项均为正数的等比数列，则 a 2 ，a n a 1 0． 【答案】D a S n1a a S  对于A选项， n n 1，所以，数列 n n 是等差数列，因此A正确； sin A(cosB 3sinB)sin A 【解析】由正弦定理知 ， a2 a2   a2 对于C选项， n 1 ， n 是常数列，且为等差数列，因此C正确； π cosB 3sinB2sin(B )1 而sinA0，∴ 6 ， S S  n a 0  n 对于D选项， n 1 ，  n 是等比数列，因此D正确； π π 7π π 5π 2π  B  B  B 又6 6 6 ，即 6 6 ，∴ 3 ， a S n1 n1 n1  对于B选项，a S na2，则 a S n 不是常数，a S  不是等比数列，因此B不正确， n n 1 n n n n 故选D． 故选B． 5．某公司为激励创新，计划逐年加大研发资金投入，若该公司2020年全年投入研发资金130万元，在 x2 y2 此基础上，每年投入的研发资金比上一年增长12%，则该公司全年投入的研发资金开始超过200万元 C:  1a0,b0 7．已知双曲线 a2 b2 的左､右焦点分别为F ，F ，P为双曲线C上的一点，若 1 2 的年份是（ ）（参考数据∶ ， ， ） lg1．120．05 lg1．30．11 lg20.30   1 A．2021年 B．2022年 C．2023年 D．2024年 MF MO b2 线段 PF 1 与y轴的交点M 恰好是线段 PF 1 的中点， 1 4 ，其中，O为坐标原点，则双曲 【答案】D n 【解析】设在2020年后第 年超过200万， 线C的渐近线方程为（ ） 2 2 1.12n  lg1.12n lg 1 则130(112%)n 200， 1.3， 1.3， A． y  2 x B．y x C．y  3x D．y 2x nlg1.12lg2lg1.3 0.05n0.300.110.19 n3.8 即 ， ， ， 【答案】B F c,0 第4年满足题意，即为2024年，故选D． 【解析】设双曲线 C 的半焦距为 c ，则点 1 ， a  S S  6．已知 n 是各项均为正数的等比数列，其前 n 项和为 n，且 n 是等差数列，则下列结论错误的 PF  x P c 由题意知 2 轴，所以点 的横坐标为 ， 是（ ） Pc,y y 0 由双曲线的对称性特点不妨设点 0 0 ， a S  a S  A． n n 是等差数列 B． n n 是等比数列 c2 y 2 b2  0 1 y  S  所以a2 b2 ，解得 0 a ， C．  a n 2 是等差数列 D．   n n 是等比数列  b2  Pc,  所以点 ， 【答案】B  a  b2  二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目 0,  所以点 的坐标为 ， M  2a 要求．全部选对的得5分，部分选对的得2分，有选错的得0分． n  1 ax2    b2    b2  9．若  展开式所有项的系数之和与二项式系数之和均为32，则下面结论正确的是（ ） MF c,  MO0,   x 所以 1  2a ，  2a ， n5 x4 A． B．展开式中含 的系数为270    b2   b2  b4 1 MF MOc,  0,   b2 故 1  2a  2a 4a2 4 ， 90x C．展开式的第4项为 D．展开式中含有常数项 a2 b2 ab 所以 ，所以 ， 【答案】ABC C y x 【解析】令x1，由题意可得 a1n 2n 32 ，∴n5，a3， 所以双曲线 的渐近线方程为 ，故选B． 5 8．过点 A2,1 作直线 l 交圆 C:x2  y2 2y170 于 M,N 两点，设  A  M    A  N  ，则实数  的取 ∴二项式为    3x2  1 x    ，∴A对； 值范围为（ ） r T Cr 3x25r  1 35r 1r Cr x103r  5, 1   5 ,1    5 , 1 ∴ r1 5   x   5 ， A．   5   B． 5,1 C．   2   D．   2 5   r=2 x4 令 ，计算可知展开式中含 的系数为270，∴B对； 【答案】A C (0,1) 3 2 T 35313 C3x1033 90x 【解析】由已知得，圆 是以 为圆心，以 为半径的圆． 令r 3，所以 4 5 ，所以展开式的第4项为90x，∴C对； AC 2 2 3 2 10  ，点A在圆的内部， r  令103r 0，解得 3 ，而rN，所以展开式中不含有常数项， 故当直线MN 经过圆心C时，取得最值． 故选ABC． MA  NA MA r CA 5 2 NA r AC  2 （1）当 时， ， ， m n   10．已知 ， 是两条不相同的直线， ， 是两个不重合的平面，则下列命题中真命题有（ ） MA  5 此时，  取最小值为 NA ； m n m//n // m m n n// A．若 ， ， ，则 B．若 ， ， ，则 MA  NA NA r CA 5 2 MA rAC  2  m mn n// // m n// mn （2）当 时， ， ， C．若 ， ， ，则 D．若 ， ， ，则 MA 1 【答案】BD   此时， 取最大值为 NA 5，    【解析】对于选项A，平面 和 可能相交，所以选项A是假命题； 1 [5, ] m m // n n// 所以， 5 ，故选A． 对于选项B，由 ， 可知 ，再由 ，可得 ，故选项B是真命题； n  对于选项C，直线 与平面 可能相交，故选项C是假命题；// m m n// mn π 对于选项D，由 ， 可知 ，再由 ，可得 ，故选项D是真命题， f(x)2sin(2x ) 所以 6 ， 故选BD．  5π π  π  2π π π π 11．函数 f x AsinxA0,0,0 π 的部分图象如图所示，则下列结论中正确 x    12 , 12  时， 2x 6     3 , 3  ， 2x 6  2 时， f(x) 2，函数 f(x)在区间 min 的是（ ）  5π π   ,    12 12上不单调，C错；  π  π π π f x 2sin2 (x ) 2sin(2x )2cos2x      6  6 6 2 是偶函数，D正确， 故选BD． 3xx3, x0 f x 12．已知函数 2x 1, x0 ，若关于 x 的方程4f 2x4a f x2a30有5个不 a 同的实根，则实数 可能的取值有（ ） 3 4 5 7     A． 2 B． 3 C． 4 D． 6 【答案】BCD f x3xx3 fx33x2 31x1x x0 【解析】当 时， ，则 ， f x 2π f x x,1 fx0 f x x1,0 fx0 f x A． 的最小正周期为 B． 的最大值为2 当 时， ， 单调递减；当 时， ， 单调递增，  5π π   π f x C． f x 在区间    12 , 12  上单调递增 D． f   x 6  为偶函数 作出 的图象，如图所示， 【答案】BD 11π 5π 2π T 2(  ) π  2 【解析】由已知 12 12 ，所以 T ，A错； 5π 2 kπ,kZ 由五点法得 12 ， π π  f(0) Asin 1 又0π，所以 6， 6 ，A2，B正确； f xt 4t2 4at2a30 令 ，则 ， gt4t2 4at2a3 gt0 令 ，由题意得方程 有两个不同的根：①有两个不同的根 t 1， t 2，且 t 1 2,1 ， t 2 1,0 ， ①由变量x和y的数据得到其回归直线方程l: yˆ b ˆ xaˆ ，则l一定经过点 P  x,y  ； g20 ②在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；  则有g10 ，解得 3 7 ； ③线性相关系数r越大，两个变量的线性相关性越强，反之，线性相关性越弱；  g00  a  2 6 y  0.5x10 x y 0.5 ④在回归直线方程 中，当解释变量 每增加一个单位时，预报变量 增加 个单位． t t t 1 t 1,0 ②有两个不同的根 1， 2，且 1 ， 2 ， 其中真命题的序号是______． 7 【答案】①② gt  g16a70 a 则有 1 ，则 6， P  x,y  【解析】回归直线一定过样本中心点 ，故①正确； 1 t  1,0 残差平方和越小，说明模型的拟合效果越好，故②正确； 方程为6t2 7t10，得 t 1 ， 2 6 ，满足条件； 1 线性相关系数r的绝对值越大，两个变量的线性相关性越强，反之，线性相关性越弱，故③错误； t t t 0 t 1,0 在回归直线方程 y  0.5x10 中，当解释变量 x 每增加一个单位时，预报变量 y 减少 0.5 个单位， ③有两个不同的根 1， 2，且 1 ， 2 ， 故④错误， 3 gt  g02a30 a  因为 1 ，则 2， 故答案为①②． f(x)ex x  x , f x  y kxb kb 15．若函数 图象在点 0 0 处的切线方程为 ，则 的最小值为 3 3 t2  t 0 t  1,0 方程为 2 ，得 t 0 ， 2 2 ，不符合题意，舍去， 1 __________． 1  3 7  1 a   ,  【答案】 e 综上所述，实数  2 6， f(x)ex x fxex 1 故选BCD． 【解析】已知 ，得 ，  x , f x  fx ex 0 1 设切点为 0 0 ，故 0 ， 第Ⅱ卷（非选择题） 故 f(x)ex x 图象在点  x 0 , f x 0  处的切线斜率为 k ex 0 1 ， 三、填空题：本大题共4小题，每小题5分． 1 0.9 2 0.63 1 所求切线方程为 y   ex 0 1 xx 0 ex 0 x 0，即 y   ex 0 1  xex 0 x 0 ex 0 ， 13．已知某种元件的使用寿命超过 年的概率为 ，超过 年的概率为 ，若一个这种元件使用 年时还未失效，则这个元件使用寿命超过2年的概率为_________． 则 k ex 0 1 ， bex 0 x 0 ex 0 ，则 kbex 0 x 0 1 ， 【答案】0.7 gx xex 1 gxexx1 令 ， ， 【解析】设一个这种元件使用1年的事件为A，使用2年的事件为B， P(AB) 0.63 gx0 gx0 P(B∣A)  0.7 当 x1 时， ；当 x1 时， ， 则 P(A) 0.9 ，故答案为0.7． gx ,1 1, 所以 在 上递减，在 上递增， 14．给出下列命题：1 即sinBcosAsin AcosB2sinCcosB， gx xex 1 1 故 在x1处取得最小值，则kb的最小值是 e ， sin(AB)sinC 2sinCcosB 即 ． 1  1 1 π cosB B 故答案为 e ． 又sinC 0，所以 2，则由0 Bπ，得 3． 22 11 3443 94249 2 16．回文数是指从左到右与从右到左读都一样的正整数，如 ， ， ， 等，显然 位回文 2 2 3 bsin A 2 a  2 2 数有9个：11，22，33， ，99，3位回文数有90个：101，111，121， ，191，202， ，999． （2）由正弦定理 a b ，得 sinB 3 ，     sin A sinB 2 （1）4位回文数有__________个． 2n1(nN ) （2）  位回文数有__________个． a2 c2 b2 8c2 12 1 cosB    则由余弦定理得 2ac 22 2c 2，解得c 2 6 (负值舍去)， 910n 【答案】90， 1 1   3 S  acsinB  2 2 2 6  3 3 【解析】（1）4位回文数的特点为中间两位相同，千位和个位数字相同但不能为零， 所以 △ABC 2 2 2 ． 第一步，选千位和个位数字，共有9种选法， 第二步，选中间两位数字，有10种选法， 18．（12分）已知数列 a n  的前 n 项和为 S n，且 a 1 2 ，当 n2 时， a n  S n 2n1 ． 故4位回文数有91090个． a  9 （1）求数列 n 的通项公式； （2）第一步，选左边第一个数字，有 种选法， b log S c b S c  T 2 3 4 n n1 101010 1010n （2）设 n 2 n，设 n n n，求数列 n 的前 n 项和为 n． 第二步，分别选左边第 、 、 、、 、 个数字，共有  种选法， 2, n1 故 2n1(nN*) 位回文数有 910n 个． 【答案】（1） a n  2n1,n2；（2）T n 2n12n1． n2 a S 2n a a S 2n S 2n1 a 2n1 【解析】（1）当 时， n1 n1 ， n1 n n1 n n1 ， 四、解答题：本大题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤． △ABC A B C a b c atanB (2ca)tan A a 2n1 17．（10分）已知在 中，内角 ， ， 所对的边分别为 ， ， ， ． 整理可得 n ， （1）求B； a 2 a 2n1 经检验： 1 不满足 n ， π A （2）若 4，b2 3，求△ABC的面积． 2, n1 a  n 2n1, n2． π 【答案】（1）3 ；（2）3 3． n2 S a 2n1 2n S a 2 S 2n （2）由（1）可知：当 时， n n ；经检验： 1 1 满足 n ， sin A sinB 2sinCsin A sin A S n 2n nN ，则 b n log 2 2n n ， c n n2n ， 【解析】（1）因为atanB (2ca)tan A，所以 cosB cosA． T 121222 323n12n1n2n  n ， 又sinA0，所以sinBcosA2sinCcosBsin AcosB，2T 122 223324 n12n n2n1 n n ， uv nuv i i  ˆ  i1 计公式分别为 n ， ． 22 12n1 u2 nu2 两式作差得 T 2n2n1  22 232n 2n2n1 i1 i  vu n 12 100 50 2n2n12n1421n2n1 yˆ 13 ， 【答案】（1） x ，13秒；（2）分布列见解析， 9 ． T 2n12n1 n ． 99994532302421 y  50 【解析】（1）由题意可知： 7 ， 333 19．（12分）三阶魔方为 的正方体结构，由26个色块组成．常规竞速玩法是将魔方打乱，然后 7 z y 7zy 在最短的时间内复原． i i 184.570.3750 55 b ˆ  i1   100 （1）某魔方爱好者进行一段时间的魔方还原训练，每天魔方还原的平均速度 y （秒）与训练天数x 7 0.55 0.55 ， z2 7z2 i （天）有关，经统计得到如下数据： i1 x （天） 1 2 3 4 5 6 7 aˆ  yb ˆ z 501000.3713 所以 ， y （秒） 99 99 45 32 30 24 21 100 yˆ 13 b 因此y关于x的回归方程为 x ， y a 现用 x ，作为回归方程类型，请利用表中数据，求出该回归方程，并预测该魔方爱好者经过长 y 所以最终每天魔方还原的平均速度 约为13秒． y 期训练后最终每天魔方还原的平均速度 约为多少秒（精确到1秒）； （2）由题意可知：X 的可能取值为3，4，6，9， （2）现有一个复原好的三阶魔方，白面朝上，只可以扭动最外侧的六个表面．某人按规定将魔方随机 A1 1 2A1 2 A1  1A1 A1A1 5 PX 3 4  PX 4 4  PX 6 4 2 2 4  ； ； ； EX 66 9 66 9 66 9 扭动两次，每次均顺时针转动 90 ，记顶面白色色块的个数为X ，求X 的分布列及数学期望 ． A1A1 1 1 PX 9 2 2  z  66 9， 参考数据（其中 i x ）． i 所以X 的分布列为 参考公式： X 3 4 6 9 7 7 z y z z2 7z2 i i i 1 2 5 1 i1 i1 P 9 9 9 9 184.5 0.37 0.55 1 2 5 1 50 EX3 4 6 9  u ,v  u ,v  u ,v  v u 所以数学期望为 9 9 9 9 9 ． 对于一组数据 1 1 ， 2 2 ，…， n n 其回归直线 的斜率和截距的最小二乘法估 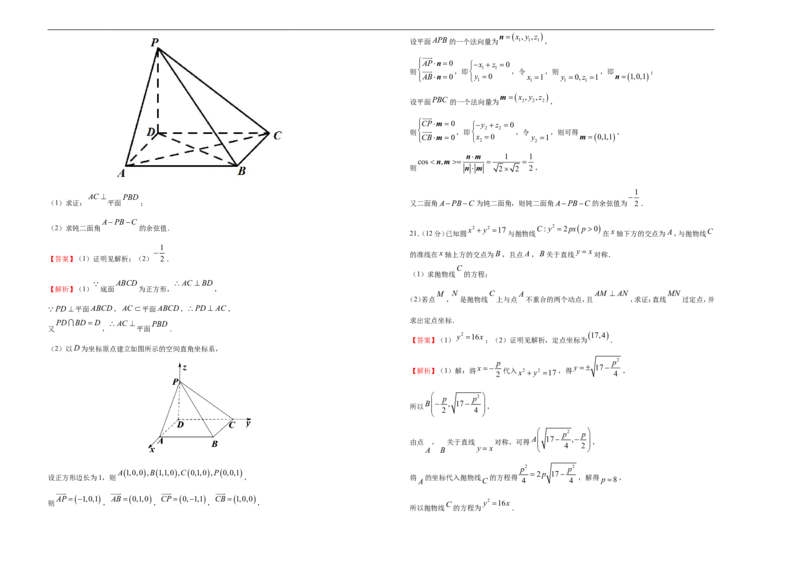PABCD ABCD PD ABCD AD PD 20．（12分）如图，在四棱锥 中，底面 为正方形， 平面 ， ．nx ,y ,z  设平面APB的一个法向量为 1 1 1 ，   APn0 x z 0 则  ，即 1 1 ，令 ，则 ，即 ； ABn0  y 0 x 1 y 0,z 1 n1,0,1 1 1 1 1 m x ,y ,z  PBC 设平面 的一个法向量为 2 2 2 ，   CPm 0 y z 0 则  ，即 2 2 ，令 ，则可得 ， CBm 0  x 0 y 1 m 0,1,1 2 2 nm 1 1 cosn,m    则 n  m 2 2 2， 1 AC  PBD  （1）求证： 平面 ； 又二面角APBC 为钝二面角，则钝二面角APBC 的余弦值为 2 ． APBC （2）求钝二面角 的余弦值． 21．（12分）已知圆 x2  y2 17 与抛物线 C: y2 2pxp 0 在 x 轴下方的交点为A，与抛物线 C 1  的准线在x轴上方的交点为B，且点A，B关于直线 y  x 对称． 【答案】（1）证明见解析；（2） 2 ． C （1）求抛物线 的方程； ABCD AC  BD  【解析】（1） 底面 为正方形， ， M N C A AM  AN MN （2）若点 ， 是抛物线 上与点 不重合的两个动点，且 ，求证：直线 过定点，并 PD平面ABCD，AC 平面ABCD，PD AC，  求出定点坐标． PD  BD D AC  PBD 又 ， 平面 ． y2 16x 17,4 【答案】（1） ；（2）证明见解析，定点坐标为 ． （2）以D为坐标原点建立如图所示的空间直角坐标系， p p2 x y  17 【解析】（1）解：将 2 代入x2  y2 17，得 4 ，  p p2  B , 17  所以  2 4 ，    p2 p  A 17 ,  由点 ， 关于直线 对称，可得  4 2 ， A B y  x   p2 p2 A1,0,0,B1,1,0,C0,1,0,P0,0,1 2p 17 设正方形边长为1，则 ， 将 A 的坐标代入抛物线 C 的方程得 4 4 ，解得 p8，     AP1,0,1 AB0,1,0 CP 0,1,1 CB 1,0,0 则 ， ， ， ， C y2 16x 所以抛物线 的方程为 ．A1,4 f xx2 x2 lnxx0 （2）证明：由（1）得 ， （2）由方程 有唯一实数解，即 有唯一实数解，  y2   y2  2x2 x1 设 M  16 1 ,y 1   ， N 16 2 ,y 2   ，直线 MN 的方程为 xmyn ． 设gxx2 lnxx，则 gx x ,x0 ， MN y2 16 y2 16my16n0 2x2 x10,x0 将直线 的方程代入 得，所以 ， 令 ， y  y 16m y y 16n 1 所以 1 2 ， 1 2 ． x x  0 因为0，所以Δ180，且 1 2 2 ，所以方程有两异号根， 因为AM  AN ，所以    y2   y2   y2 16  y2 16  设 x 1 0 ， x 2 0 ，因为 x0 ，所以 x 1应舍去， AM AN  16 1 1,y 1 4   16 2 1,y 2 4   1 256 2 y 1 4y 2 40 ， x0,x  gx0 gx 0,x  当 2 时， ， 在 2 上单调递减； y 4 y 4 y 4y 40 由题意可知 1 ， 2 ，所以 1 2 ． xx , gx0 gx x , 当 2 时， ， 在 2 上单调递增， y 4y 4 1 2 10 所以 256 ，即y 1 y 2 4y 1  y 2 2720， 当 x x 2时， gx 2 0 ， gx 取最小值 gx 2  ， 所以16n64m2720，即n4m17， gx 0 x2 lnx x 0 所以直线 MN 的方程为 xmy417 ， 因为 gx0 有唯一解，所以 gx 2 0 ，则   gx 2 2 0 ，即  2 2 x 2 2 x 2 2 1 2 0 ， MN 17,4 因为 0 ，所以 2lnx 2 x 2 10 ．（*） 直线 过定点，定点坐标为 ． hx2lnxx1 1 f xlnx ax2 bx 设函数 ， 22．（12分）设函数 2 ． hx hx0 x0 因为当 时， 是增函数，所以 至多有一解， f x P  1, f 1 y 2x1 a b （1）已知 在点 处的切线方程是 ，求实数 ， 的值； h10 x 1 因为 ，所以方程（*）的解为 2 ， f xx20  （2）在第（1）问的条件下，若方程 有唯一实数解，求实数 的值． x 1 2x2 x 10 1 将 2 代入 2 2 ，可得 ． a0 b1 1 【答案】（1） ， ；（2） ． 1 f 1 ab1 【解析】（1）当x1时，可得y 2111，所以 2 ，即a2b2， 1 fx axb f11ab2 因为 x ，即 ，即ab1， a2b2  联立方程组 ab1 ，解得 a0 ， b1 ．