文档内容
期中检测卷 01
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.已知等差数列{a},S 是其前n项和,若S =a =10,则( )
n n 10 10
A.a=2 B.a=﹣2 C.S=18 D.S=﹣20
5 5 5 5
【答案】D
【分析】设数列{a}的公差为d,由题意可得 ,解得a =﹣8,d=2,再根
n 1
据通项公式和求和公式即可求出.
【解答】解:设数列{a}的公差为d,由题意可得 ,
n
解得a=﹣8,d=2,
1
∴a=a+4d=0,
5 1
S= =﹣20,
5
故选:D.
【知识点】等差数列的前n项和
2.若正项等比数列{a},中,a•a=a,a=27,则该数列的公比为( )
n 1 3 2 5
A. B.1 C.3 D.9
【答案】C
【分析】根据题意,设数列{a}的公比为q,将a•a=a,变形可得(a)2=a,解可得a 的值,又由q3=
n 1 3 2 2 2 2
1 / 17,计算可得答案.
【解答】解:根据题意,设数列{a}的公比为q,
n
若a•a=a,则有(a)2=a,解可得a=1或0(舍),
1 3 2 2 2 2
a=27,则q3= =27,
5
则q=3,
故选:C.
【知识点】等比数列的通项公式
3.如图,点A(x ,f(x )),B(x ,f(x ))在函数f(x)的图象上,且x <x ,f′(x)为f(x)的导
1 1 2 2 2 1
函数,则f′(x)与f′(x)的大小关系是( )
1 2
A.f′(x)>f′(x) B.f′(x)<f′(x)
1 2 1 2
C.f′(x)=f′(x) D.不能确定
1 2
【答案】A
【分析】根据题意,由导数的几何意义可得f′(x)为点A处切线的斜率,f′(x)为点B处切线的斜率,
1 2
结合函数的图象分析切线的斜率,比较即可得答案.
【解答】解:根据题意,点A(x,f(x)),B(x,f(x),f′(x)为f(x)的导函数,
1 1 2 2
则f′(x)为点A处切线的斜率,设其斜率为k,
1 1
f′(x)为点B处切线的斜率,设其斜率为k,
2 2
由函数的图象可得k>k,
1 2
即有f′(x)>f′(x);
1 2
故选:A.
【知识点】导数及其几何意义
2 / 174.已知等比数列{a}的前n项和为S,且满足a=2,S﹣S= ,则数列{a}的前4项和为( )
n n 1 4 3 n
A. B. C. D.
【答案】A
【分析】根据题意,设等比数列{a}的公比为q,分析可得a = ,由等比数列的通项公式可得q的值,
n 4
进而由等比数列的前n项和公式计算可得答案.
【解答】解:根据题意,设等比数列{a}的公比为q,
n
若a=2,S﹣S= ,即a= ,
1 4 3 4
则q3= = ,则q= ,
故数列{a}的前4项和S= = ,
n 4
故选:A.
【知识点】等比数列的前n项和
5.已知函数f(x)在x 处的导数为f′(x),则 等于( )
0 0
A.mf′(x) B.﹣mf′(x) C. D.
0 0
【答案】A
【 分 析 】 根 据 题 意 , 由 极 限 的 运 算 性 质 可 得 = m
,结合导数的定义计算可得答案.
【解答】解:根据题意, =m =mf′(x),
0
故选:A.
【知识点】导数及其几何意义
6.设函数f'(x)是偶函数f(x)(x R)的导数,f(1)=1,当x<0时,xf'(x)+f(x)>0,则使|f(x)|
∈
3 / 17> 成立的x的取值范围是( )
A.(﹣1,0)∪(1,+∞) B.(﹣1,1)
C.(﹣∞,﹣1)∪(1,+∞) D.(﹣∞,﹣1)∪(0,1)
【答案】C
【分析】设F(x)=xf(x),根据函数的单调性和奇偶性问题转化为|F(x)|>F(1)=1,求出不等式
的解集即可.
【解答】解:设F(x)=xf(x),
易知函数F(x)为奇函数,且当x<0时,F′(x)=xf′(x)+f(x)>0,
故函数F(x)在R递增,
将目标不等式转化为|F(x)|>F(1)=1,
结合函数的单调性得:|x|>1,解得:x<﹣1或x>1,
故不等式的解集是(﹣∞,﹣1)∪(1,+∞),
故选:C.
【知识点】利用导数研究函数的单调性
7.《九章算术》第三章“衰分”介绍比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比
例为“衰分比”.如:已知A,B,C三人分配奖金的衰分比为20%,若A分得奖金1000元,则B,C
所分得奖金分别为800元和640元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得单位奖励
68780元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金 36200元,则“衰
分比”与丁所获得的奖金分别为( )
A.20%,14580元 B.10%,14580元
C.20%,10800元 D.10%,10800元
【答案】B
【分析】根据题意,设甲、乙、丙、丁获得的奖金组成等比数列{a},设“衰分比”为m,则数列的公比
n
为1﹣m,由等比数列的通项公式可得 ,进而计算可得m与a 的值,即
4
可得答案.
【解答】解:根据题意,设甲、乙、丙、丁获得的奖金组成等比数列{a},设“衰分比”为m,则数列的
n
公比为1﹣m,
则有 ,则有a+a=32580,
2 4
则有1﹣m=0.9,则m=0.1=10%,
4 / 17则有 +a=32580,解可得a=14580,
4 4
即“衰分比”为10%,丁所获得的奖金14580,
故选:B.
【知识点】等比数列的通项公式
8.设f'(x)是函数f(x)的导函数,若f'(x)>0,且∀x,x R(x≠x),f(x)+f(x)<2f(
1 2 1 2 1 2
∈
),则下列各项中不一定正确的是( )
A.f(2)<f(e)<f( )
B.f′( )<f′(e)<πf′(2)
C.f(2)π<f′(2)﹣f′(3)<f(3)
D.f′(3)<f(3)﹣f(2)<f′(2)
【答案】C
【 分 析 】 f′ ( x ) > 0 , ∴ f ( x ) 在 R 上 单 调 递 增 , 由
, 可 得 <
,可得y=f(x)的图象如图所示,图象是向上凸.进而判断出正误.
【解答】解:∵f′(x)>0,∴f(x)在R上单调递增,
∵ ,
∴ < ,
∴y=f(x)的图象如图所示,图象是向上凸.
∴f(2)<f(e)<f( ),f′( )<f′(e)<f′(2),可知:A,B正确.
π π
∵f(3)﹣f(2)= ,表示点A(2,f(2)),B(3,f(3))的连线的斜率.
由图可知:f′(3)<k <f′(2),故D正确.
AB
C项无法推出,
故选:C.
5 / 17【知识点】利用导数研究函数的单调性
二、多选题(本大题共4小题,每小题5分,共20分)在每小题所给出的四个选项中,有多项是符合题目
要求的;错选或多选不得分。
9.已知{a}为等差数列,其前n项和S,a+a<0,则下列结论一定正确的是( )
n n 7 8
A.若a>0,则公差d<0 B.若a<0,则S 最小
1 1 7
C.S <0 D.S <0
15 14
【答案】AD
【分析】由题意利用等差数列的求和公式以及等差数列的性质,得出结论.
【解答】解:A、当a>0时,因为a+a=2a+13d<0,所以d<0,故A正确.
1 7 8 1
B、当a<0,d<0时,满足a+a<0,S 无最小值,故B错误.
1 7 8 n
C、当a >0,d<0,且满足a+a <0时,a <0,此时S =15a ,当a <0,d>0,且满足
1 7 8 8 15 8 1
a+a<0时,a 的符号无法确定,故C错误.
7 8 8
D、S =7(a+a)<0,故D正确.
14 7 8
故选:AD.
【知识点】等差数列的前n项和
10.设等比数列{a}的公比为q,其前n项和为S ,前n项积为T ,并满足条件a >1,且a a >1,
n n n 1 2020 2021
(a ﹣1)(a ﹣1)<0,下列结论正确的是( )
2020 2021
A.S <S
2020 2021
B.a a ﹣1<0
2020 2022
C.数列{T}无最大值
n
D.T 是数列{T}中的最大值
2020 n
【答案】ABD
【分析】根据题意,分析可得a >1,a <1,从而有a>1,0<q<1,则等比数列{a}为正项的递减数
2020 2021 1 n
列.再结合等比数列的性质逐一核对四个命题得答案即可得到正确选项.
6 / 17【解答】解:根据题意,根据题意,等比数列{a}的公比为q,若a a >1,则(aq2019)(aq2020)=
n 2020 2021 1 1
(a)2(q4039)>1,
1
又由a>1,必有q>0,则数列{a}各项均为正值,
1 n
若(a ﹣1)(a ﹣1)<0,必有a >1,0<a <1,则必有0<q<1,
2020 2021 2020 2021
依次分析选项:
对于A,数列{a}各项均为正值,则S ﹣S =a >0,必有S <S ,A正确;
n 2021 2020 2021 2020 2021
对于B,若0<a <1,则a a ﹣1=(a )2﹣1<0,B正确,
2021 2020 2022 2021
对于C,根据a>a>…>a >1>a >…>0,可知T 是数列{T}中的最大项,C错误;
1 2 2020 2021 2020 n
对于D,易得D正确,
故选:ABD.
【知识点】等比数列的前n项和
11.已知函数f(x)=xln(1+x),则( )
A.f(x)在(0,+∞)单调递增
B.f(x)有两个零点
C.曲线y=f(x)在点(﹣ ,f(﹣ ))处切线的斜率为﹣1﹣ln2
D.f(x)是偶函数
【答案】AC
【分析】先对函数求导,然后结合导数与单调性关系,导数的几何意义及函数性质分别检验各选项即可判
断.
【解答】解:函数定义域(﹣1,+∞),不关于原点对称,D错误,
因为 ,
当x<0时,f′(x)>0恒成立,f(x)单调递增,A正确,
= ,
当x>﹣1时,f″(x)>0,f′(x)单调递增且f′(0)=0,
故当x (﹣1,0)时,f′(x)<0,f(x)单调递减,当x (0,+∞)时,f′(x)>0,f
(x)单调递增,
∈ ∈
又f(0)=0,
所以f(x)只有一个零点,B正确,
因为f′(﹣ )=ln ﹣1=﹣1﹣ln2,C 正确.
故选:AC.
【知识点】导数及其几何意义、利用导数研究函数的单调性
12.已知f'(x)为函数f(x)的导函数,f'(x)=3x2+6x+b,且f(0)=0,若g(x)=f(x)﹣2xlnx,求
7 / 17使得g(x)>0恒成立b的值可能为( )
A.﹣2ln2﹣ B.﹣ln2﹣ C.0 D.ln2﹣
【答案】BCD
【分析】求出函数f(x)的解析式,从而求出g(x)的解析式,问题转化为b>2lnx﹣x2﹣3x,设 (x)
=2lnx﹣x2﹣3x(x (0,+∞)),根据函数的单调性求出b的范围即可.
φ
【解答】解:∵f'(x)=3x2+6x+b,
∈
∴可设f(x)=x3+3x2+bc+c,又f(0)=0,故c=0,
从而f(x)=x3+3x2+bx,
∴g(x)=f(x)﹣2xlnx=x3+3x2+bx﹣2xlnx,
则g(x)的定义域是(0,+∞),
则g(x)>0可化为x2+3x+b﹣2lnx>0,即b>2lnx﹣x2﹣3x,
设 (x)=2lnx﹣x2﹣3x(x (0,+∞)),
φ ∈
则 ′(x)= ﹣2x﹣3= ,
φ
令 ′(x)>0,解得:0<x< ,令 ′(x)<0,解得:x> ,
φ φ
故 (x)在(0, )递增,在( ,+∞)递减,
φ
故当x= 时, (x)取得最大值 ( )=﹣2ln2﹣ ,
φ φ
要使g(x)>0恒成立,则b>﹣2ln2﹣ 即可,
故选:BCD.
【知识点】利用导数研究函数的最值
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知等差数列{a}的首项为3,公差为2,则a = .
n 10
【答案】21
【分析】由已知结合等差数列的通项公式即可直接求解.
【解答】解:因为等差数列{a}的首项为3,公差为2,
n
则a =a+9d=3+9×2=21.
10 1
故答案为:21.
【知识点】等差数列的通项公式
14.曲线f(x)=sinxcos2x在点( ,f( ))处的切线方程为 .
8 / 17【分析】求得f(x)的导数,由导数的几何意义可得切线的斜率,求得切点,由直线的点斜式方程可得所
求切线的方程.
【解答】解:f(x)=sinxcos2x的导数为f′(x)=cosxcos2x﹣2sinxsin2x,
可得在点( ,f( ))处的切线斜率为k=f′( )=cos cos ﹣2sin sin =
﹣ ,
又f( )=sin cos =0,
可得切线的方程为y=﹣ (x﹣ ),即为4x+2 y﹣ =0.
故答案为:4x+2 y﹣ =0.
π
【知识点】利用导数研究曲线上某点切线方程
π
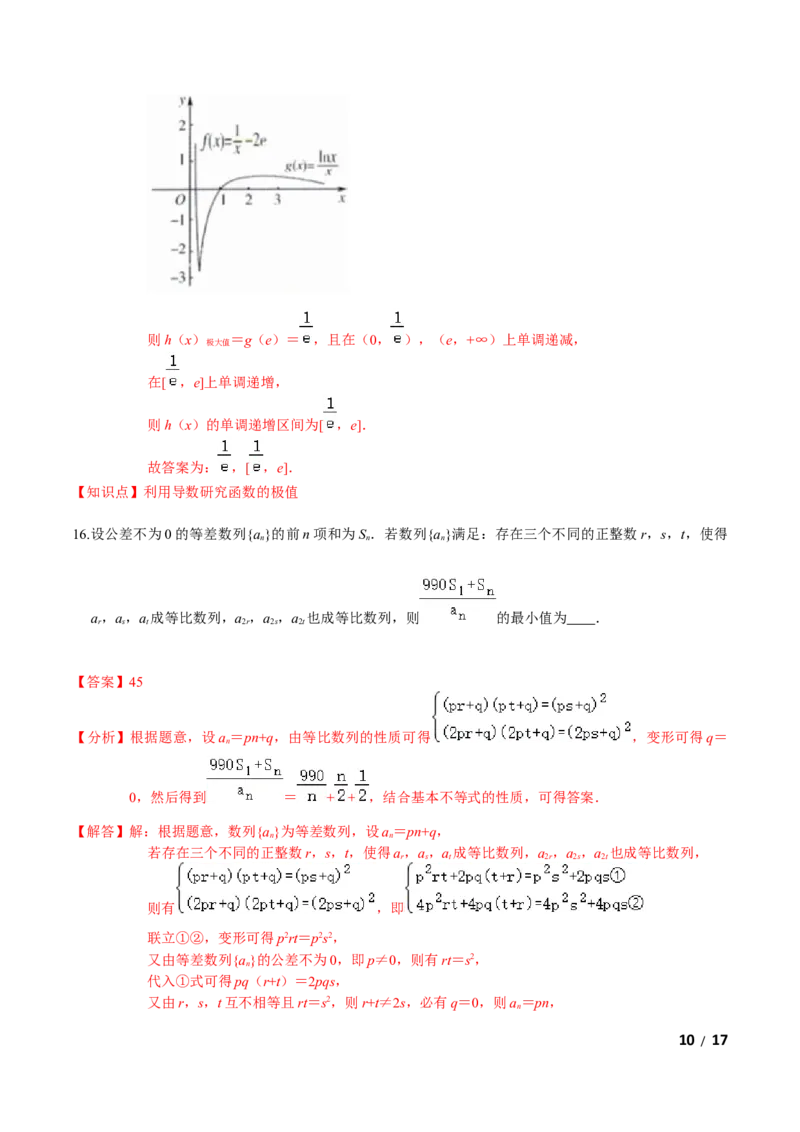
15.定义max{a,b}= 且f(x)= ﹣2e,g(x)= ,令h(x)=max{f(x),g(x)},
则h(x)的极大值为 ,单调递增区间为 .
【分析】对g(x)求导,分析g′(x)的正负,g(x)的单调性,作出h(x)=max{f(x),g(x)}的
大致图象如下:
h(x)的单调递增区间为[ ,e].
【解答】解:因为g(x)= (x>0),
所以g′(x)= ,
令g′(x)=0,则x=e,
当0<x<e时,g′(x)>0,g(x)单调递增,
当x>e时,g′(x)<0,g(x)单调递减,
所以g(x) =g(e)= ,
极大值
由f(x)=g(x),即x﹣2e= ,得x= ,
作出h(x)=max{f(x),g(x)}的大致图象如下:
9 / 17则h(x) =g(e)= ,且在(0, ),(e,+∞)上单调递减,
极大值
在[ ,e]上单调递增,
则h(x)的单调递增区间为[ ,e].
故答案为: ,[ ,e].
【知识点】利用导数研究函数的极值
16.设公差不为0的等差数列{a}的前n项和为S .若数列{a}满足:存在三个不同的正整数r,s,t,使得
n n n
a,a,a成等比数列,a ,a ,a 也成等比数列,则 的最小值为 .
r s t 2r 2s 2t
【答案】45
【分析】根据题意,设a =pn+q,由等比数列的性质可得 ,变形可得q=
n
0,然后得到 = + + ,结合基本不等式的性质,可得答案.
【解答】解:根据题意,数列{a}为等差数列,设a=pn+q,
n n
若存在三个不同的正整数r,s,t,使得a,a,a成等比数列,a ,a ,a 也成等比数列,
r s t 2r 2s 2t
则有 ,即
联立①②,变形可得p2rt=p2s2,
又由等差数列{a}的公差不为0,即p≠0,则有rt=s2,
n
代入①式可得pq(r+t)=2pqs,
又由r,s,t互不相等且rt=s2,则r+t≠2s,必有q=0,则a=pn,
n
10 / 17所以S=a=p,S= = ,
1 1 n
故 = = + + ,
设f(n)= + + ,
则f(n)= + + ≥2 + =2 + ,
当且仅当n2=1980时等号成立,此时n不是正整数,不符合题意,
而44< <45,
所以f(44)= + + =45,f(45)= + + =45,
则有f(45)=f(44),即 的最小值为45,
故答案为:45.
【知识点】等比数列的性质、数列与不等式的综合、等比数列的前n项和
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.△ABC的内角A,B,C的对边分别为a,b,c,角A,B,C成等差数列,a=2.
(1)若c=1,求b;
(2)若△ABC的面积为 ,求c.
【分析】(1)由A,B,C成等差数列及三角形内角和为 可得B的值,在三角形中由余弦定理可得b的
值;
π
(2)由三角形的面积公式求出c边.
【解答】解:(1)因为角A,B,C成等差数列,所以2B=A+C,而A+B+C= ,
π
所以B= ,
因为a=2,c=1,由余弦定理可得b= = = ;
(2)因为S = acsinB= = c= ,
△ABC
所以c=2.
【知识点】余弦定理、等比数列的通项公式
11 / 1718.已知函数f(x)=x3+ax2﹣a2x+1,a R.
(1)当a=1时,求函数f(x)在区间∈[﹣2,1]上的最大值;
(2)当a≥0时,求函数f(x)的极值.
【分析】(1)将a=1代入,求导,求出函数在[﹣2,1]上的单调性,进而求得最大值;
(2)求导,分a=0及a>0两种情形讨论即可得出结论.
【解答】解:(1)当a=1时,f(x)=x3+x2﹣x+1,则f′(x)=3x2+2x﹣1=(x+1)(3x﹣1),
令f′(x)>0,解得﹣2<x<﹣1或 ,令f′(x)<0,解得 ,
∴函数f(x)在 单调递增,在 单调递减,
由于f(﹣1)=2,f(1)=2,故函数f(x)在区间[﹣2,1]上的最大值为2;
(2)f′(x)=3x2+2ax﹣a2=(x+a)(3x﹣a),令f′(x)=0,解得x=﹣a或 ,
当a=0时,f′(x)=3x2≥0,所以函数f(x)在R上递增,无极值;
当a>0时,令f′(x)>0,解得x<﹣a或 ,令f′(x)<0,解得 ,
∴函数f(x)在(﹣∞,﹣a), 单调递增,在 单调递减,
∴函数f(x)的极大值为f(﹣a)=a2+1,极小值为 .
【知识点】利用导数研究函数的最值、利用导数研究函数的极值
19.已知函数f(x)=x2﹣(2+a)x+alnx(a R).
(1)当a>0时,讨论f(x)的单调区间;∈
(2)若对∀x (0,+∞),f(x)≥(a+1)lnx﹣2x成立,求实数a的取值范围.
∈
【分析】(1)先对函数求导,然后结合导数与单调性的关系对a进行分类讨论,确定导数的符号,即可求
解函数的单调性;
(2)由已知不等式恒成立,分离参数后转化为求解相应函数的范围,构造函数,结合导数可
求.
【解答】解:(1)函数的定义域(0,+∞), = ,
①当0< 即0<a<2时,当x ,(1,+∞)时,f′(x)>0,函数单调递
增,
当x 时,f′(x)<0,函数单调递减,
②当 即a=2时,f′(x)= ≥0恒成立,故f(x)在(0,+∞)上单调递增,
12 / 17③当 即a>2时,x 时,f′(x)<0,函数单调递减,
当x 时,f′(x)>0,函数单调递增;
综上可得,当0<a<2时,函数的单调递增区间(0, ),(1,+∞),单调递减区间(
);
当a=2时,函数的单调递增区间(0,+∞),没有递减区间;
当a>2时,函数的单调递增区间(0,1),( ,+∞),单调递减区间(1, );
(2)因为∀x (0,+∞),f(x)≥(a+1)lnx﹣2x成立,
所以,x2﹣(a+2)x+alnx≥(a+1)lnx﹣2x成立,即x2﹣ax﹣lnx≥0恒成立,
∈
所以a ,
令g(x)= ,x>0,
则 ,
令h(x)=x2+lnx﹣1,x>0,则 ,
所以h(x)在(0,+∞)上单调递增,且h(1)=0,
所以当0<x<1时,h(x)<0,即g′(x)<0,函数g(x)单调递减,当x>1时,h(x)
>0,即g′(x)>0,函数g(x)单调递增,
故当x=1时,g(x)取得最小值g(1)=1,
所以a≤1.
【知识点】利用导数研究函数的单调性、利用导数研究函数的最值
20.已知数列{a}满足aa…a=1﹣a.
n 1 2 n n
(1)求证数列{ }是等差数列,并求数列{a}的通项公式;
n
(2)设T=aa……a,b=a2T2,证明:b+b+…+b< .
n 1 2 n n n n 1 2 n
【分析】(1)先由题设⇒a = ,再利用等差数列的定义证明结论,然后求得a,进而求得a;
n+1 1 n
(2)先由(1)求得T 与b,再利用放缩法与裂项相消法证明结论即可.
n n
【解答】证明:(1)∵aa…a=1﹣a ,∴aa…a =1﹣a ,
1 2 n n 1 2 n+1 n+1
① ②
13 / 17由 得:a = ,即a = ,a ﹣1= ﹣1= ,
n+1 n+1 n+1
∴ = = ﹣1,
∴ ﹣ =﹣1,
又当n=1时,有a=1﹣a,解得:a= ,∴ =﹣2,
1 1 1
∴数列{ }是以﹣2为首项,﹣1为公差的等差数列,
∴ =﹣2﹣(n﹣1)=﹣1﹣n,
∴a= ;
n
(2)由(1)可得:T=aa…a= × ×…× = ,
n 1 2 n
b = ( ) 2× ( ) 2 = = = < <
n
= ﹣ ,
∴b+b+…+b< ﹣ + ﹣ +…+ ﹣ = ﹣ < .
1 2 n
【知识点】数列递推式、等差数列的性质
21.已知函数f(x)=ax2+bx+c,f(x)=ex.
1 2
(1)当a= ,b=1,c=0时,设f(x)=mf (x)﹣f(x),且函数f(x)在R上单调递增.
2 1
①求实数m的取值范围;
②设h(x)=(x2﹣3m)f(x),当实数m取最小值时,求函数h(x)的极小值.
2
(2)当a=0,b>1,c=1时,证明:函数g(x)=f(x)﹣f(x)有两个零点.
2 1
14 / 17【分析】(1)①求导得到f′(x)=mex﹣x﹣1≥0恒成立,即m≥ 在R上恒成立,设 (x)=
φ
,求函数的最大值得到答案.h(x)=(x2﹣3)ex.求导得到函数单调性,得到极小值.
②由①可知,m=1,则h(x)=(x2﹣3)ex.求导数,得到极值点,分析单调性,进而求出h
(x)的极小值.
(2)根据题意得,函数g(x)=ex﹣bx﹣1(b>1),求导数,分析单调性,得到g(x) =
min
g(lnb)=b﹣blnb﹣1(b>1),令p(b)=b﹣blnb﹣1(b>1),通过求导数,分析单调性,
得到g(x) =g(lnb)<0,g(b)=eb﹣b2﹣1(b>1),求导数分析单调性,得当b>1时,
min
0<lnb<b,所以由零点存在性定理知,存在lnb<x <b,使得g(x )=0.又g(0)=0,所
1 1
以g(x)由两个零点.
【解答】解:(1)①f(x)=mex﹣ ﹣x,得f′(x)=mex﹣x﹣1,
由题意知f′(x)≥0在R上恒成立,∴m≥ 在R上恒成立.
令 (x)= ,则m≥ (x) , ′(x)=﹣ ,
max
φ φ φ
令 (x)>0,得x<0,令 ′(x)<0得x>0,
∴ (x)在(﹣∞,0)上单调递增,在(0,+∞)单调递减,∴ (x) = (0)=1
max
φ φ
∴m≥1,即实数m的取值范围是[1,+∞).
φ φ φ
②当实数m取最小值时,m=1,∴h(x)=(x2﹣3)ex.
h′(x)=2xex+(x2﹣3)ex=(x2+2x﹣3)ex,
令h′(x)=0,解得x=1或x=3
当x<﹣3或x>1时,h′(x)>0当﹣3<x<1时,h′(x)<0.
∴h(x)在(﹣∞,﹣3)上单调递增,在(﹣3,1)上单调递减,在(1,+∞)上单调递增,
∴当x=1时,h(x)取得极小值,极小值为﹣2e.
(2)当a=0,c=1时,函数g(x)=ex﹣bx﹣1(b>1),g′(x)=ex﹣b
令g′(x)=0,解得x=lnb,
当x<lnb时,g′(x)<0,g(x)在(﹣∞,lnb)上单调递减,
当x>lnb时,g′(x)>0,g(x)在(lnb,+∞)上单调递增,
∴g(x) =g(lnb)=b﹣blnb﹣1(b>1)
min
令p(b)=b﹣blnb﹣1(b>1),
则p′(b)=1﹣lnb﹣1=﹣lnb<0,
∴p(b)在(1,+∞)上单调递减,
∴p(b)<0,即∴g(x) =g(lnb)<0,
min
g(b)=eb﹣b2﹣1(b>1)
令r(b)=eb﹣b2﹣1(b>1),则r′(b)=eb﹣2b,
令t(b)=eb﹣2b(b>1),则t′(b)=eb﹣2,
因为b>1,∴t′(b)=eb﹣2>0,
∴r′(b)=eb﹣2b在(1,+∞)上单调递增,∴r′(b)>0.
r(b)在(1,+∞)上单调递增,所以r(b)>0,即g(b)>0.
15 / 17又当b>1时,0<lnb<b
所以由零点存在性定理知,存在lnb<x<b,使得g(x)=0.
1 1
又g(0)=0,∴g(x)有两个零点.
【知识点】利用导数研究函数的单调性、利用导数研究函数的最值
22.已知公差大于0的等差数列{a}的前n项和为S,且满足a•a=﹣9,a+a=﹣8.
n n 3 8 5 6
(1)求数列{a}的通项公式a;
n n
(2)若T=|a|+|a|+|a|+…+|a|,求T 的表达式;
n 1 2 3 n n
(3)若 ,存在非零常数c,使得数列{b}是等差数列,存在n N*,不等式 成立,
n
∈
求k的取值范围.
【分析】(1)根据题意,由等差数列的性质可得a、a 的值,据此求出d和a,计算可得答案,
3 8 1
(2)由(1)的结论可得数列的前7项均为负数,从第8项开始都为正数.据此分2种情况求
出T,综合可得答案,
n
(3)根据题意,求出S,即可得数列{b}的通项,由等差数列的性质分析c的值,即可得b=
n n n
n,据此不等式不等式 等价于 成立.则只需 成立,结
合基本不等式的性质分析可得答案.
【解答】解:(1)根据题意,因为数列{a}是等差数列,设其公差为d,
n
则有a+a=a+a=﹣8,又由a•a=﹣9,
3 8 5 6 3 8
则有a=1,a=﹣9或a=﹣9,a=1,
3 8 3 8
因为d>0,故可得a=﹣9,a=1,则5d=a﹣a=10,
3 8 8 3
解得d=2,a=a+2d=﹣9,故a=﹣13.故a=2n﹣15.
3 1 1 n
(2)根据(1)中所求,令a=2n﹣15>0,解得n>7.5,
n
故数列的前7项均为负数,从第8项开始都为正数.
当n≤7时, ;
当n>7时, .
综上所述: .
(3)由(1)中a=2n﹣15.则 ,
n
故可得 ,因为存在非零常数,使得其为等差数列,
16 / 17故可得b+b =2b ,即 ,整理得c2+14c=0,解得c=﹣14,c=0舍去.故
1 3 2
.
则存在n N*,不等式 成立,等价于存在n N*,
∈ ∈
不等式 成立.则只需 ,
且当n=3时, ;当n=4时, ,
故 的最小值为 ,则 即可;
故k的取值范围为( ,+∞).
【知识点】等差数列的通项公式、等差数列的前n项和、数列与不等式的综合
17 / 17