拓展四导数与零点、不等式的综合运用（精讲）（解析版）_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第二套）

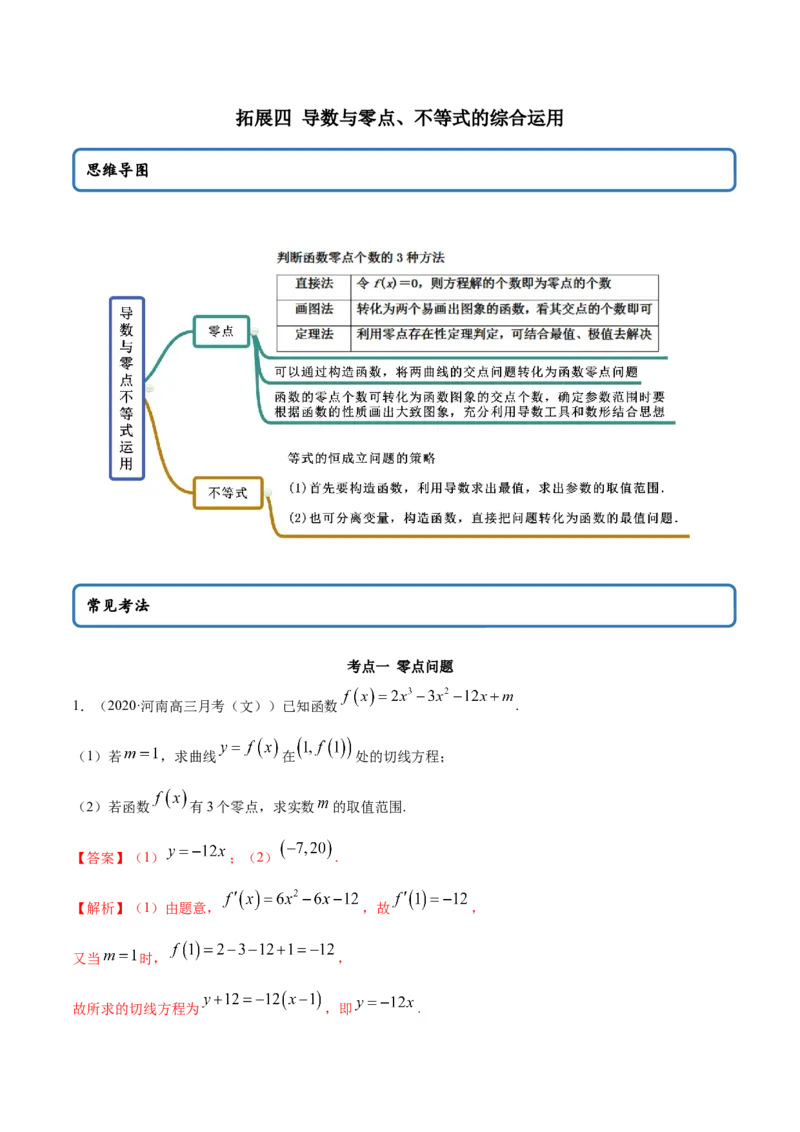
拓展四 导数与零点、不等式的综合运用 思维导图 常见考法 考点一 零点问题 1．（2020·河南高三月考（文））已知函数 . （1）若 ，求曲线 在 处的切线方程； （2）若函数 有3个零点，求实数 的取值范围. 【答案】（1） ；（2） . 【解析】（1）由题意， ，故 ， 又当 时， ， 故所求的切线方程为 ，即 .（2）由题意， ， 令 ，得 或 ， 故当 时， ，当 时， ，当 时， 故当 时，函数 有极大值 ， 当 时，函数 有极小值 . 若函数 有3个零点，实数 满足 ，解得 ， 即实数 的取值范围为 . 【一隅三反】 1．（2020·山西运城·）已知函数 . （1）讨论 的单调性； （2）若 有两个零点，求 的取值范围. 【答案】（1）答案不唯一，具体见解析；（2） . 【解析】（1）函数 ，定义域为 ， ， 当 时， . 故 在定义域 上单调递增，此时无减区间. 当 时，令 ，得 ； 当 时， ，故 单调递增；当 时， ，故 单调递减. 综上所述，当 时， 在定义域 上单调递增，此时无减区间； 当 时， 在 上单调递增，在 上单调递减. （2）由（1）知， 时， 至多一个零点，不符合题意； 当 时， 在 上单调递增，在 上单调递减. 要有两个零点，需满足 ，即 . 此时 ， . 因为 ，所以 在 有一个零点； 因为 ， . 令 ， ， 所以 在 单调递增， ， 所以 ，所以 在 上有一个零点. 所以 ， 有两个零点. 2．（2020·陕西安康·高三三模（理））已知函数 .（1）证明：函数 在 上存在唯一的零点； （2）若函数 在区间 上的最小值为1，求 的值. 【答案】（1）证明见解析；（2） 【解析】（1）证明：∵ ，∴ . ∵ 在区间 上单调递增， 在区间 上单调递减， ∴函数 在 上单调递增. 又 ，令 ， ， 则 在 上单调递减， ，故 . 令 ，则 所以函数 在 上存在唯一的零点. （2）解：由（1）可知存在唯一的 ，使得 ，即 （*）. 函数 在 上单调递增. ∴当 时， ， 单调递减；当 时， ， 单调递增. ∴ . 由（*）式得 .∴ ，显然 是方程的解. 又∵ 是单调递减函数，方程 有且仅有唯一的解 ， 把 代入（*）式，得 ，∴ ，即所求实数 的值为 . 3．（2020·甘肃武威）设函 ， ． （1）设 ，求函数 的极值； （2）若 ，试研究函数 的零点个数． 【答案】（1）分类讨论，答案见解析；（2）1个． 【解析】（1） ， ， ， ． ， ①当 时， 恒成立， 在 上是增函数，无极值． ②当 时， ， 当 时， 单调递减；当 时， 单调递增， 的极小值 ，无极大值． （2）由（1）知，当 时， 的极小值 ， 结合 的单调性可知 ，即 恒成立． 在 上是增函数， ， ， 在 ， 中有一个零点，函数 的零点个数为1个． 考点二 导数与不等式 【例2】．（2021·湖南湘潭·月考（理））已知函数 ． （1）求 的最大值； （2）当 时， 恒成立，求a的取值范围． 【答案】（1） ；（2） . 【解析】（1）因为 ，所以 ， 设 ，所以 ，所以 在 上单调递减，且 ， 所以当 时， ，当 时， ， 所以 在 上单调递增，在 上单调递减， 所以 ； （2）因为 ，所以 ，所以当 时， 且 ，所以 恒成立， 当 时，若 恒成立，则 恒成立（*）， 设 ，所以 ，又因为 ，所以 ，所以 在 上单调递增，所以 ， 又因为由（1）知 且 ， 所以若（*）成立，只需要 ，所以 ， 综上可知： . 不等式恒成立求解参数范围的方法： （1）分离参数并构造函数解决问题； （2）采用分类讨论的方式解决问题. 【一隅三反】 1．（2019·广东湛江·高二期末（文））已知函数 ． （1）当 时，求函数 的单调区间； （2）是否存在实数 ，使 恒成立，若存在，求出实数 的取值范围；若不存在，说明理由． 【答案】（1）见解析； （2）当 时，使 恒成立． 【解析】函数 的定义域为 ， ， 当 时， 由 ，得 ，或 ，由 ，得 ， 故函数 的单调递增区间为 和 ，单调递减区间为 ， 当 时， 恒成立， 故函数 的单调递增区间为 . （2） 恒成立等价于 恒成立， 令 ， 当 时，即当 时， ， 故 在 内不能恒成立， 当 时，即当 时，则 ， 故 在 内不能恒成立， 当 时，即当 时， ， 由 解得 ， 当 时， ； 当 时， . 所以 ，解得 . 综上，当 时， 在 内恒成立，即 恒成立， 所以实数 的取值范围是 . 2．（2020·黑龙江萨尔图·大庆实验中学高二期末（文））已知函数 . （1）求 的单调区间和极值； （2）若对任意 恒成立，求实数 的最大值. 【答案】（1） 在 处取得极小值，极小值为 .（2）4 【解析】（1） ， ， ∴ 的单调增区间是 ，单调减区间是 . ∴ 在 处取得极小值，极小值为 . （2）由 变形，得 恒成立， 令 ， ， 由 .所以， 在 上是减函数，在 上是增函数. 所以， ，即 ，所以 的最大值是 . 3．（2020·安徽省含山中学月考（理））已知函数 . （1）当 时，求曲线 在点 处的切线方程； （2）求函数 的单调区间； （3）若对任意的 ，都有 成立，求a的取值范围. 【答案】（1） ；（2）答案见解析；（3） . 【解析】（1） 时， ， ， ， 曲线 在点 处的切线方程 （2） ①当 时， 恒成立，函数 的递增区间为 ②当 时，令 ，解得 或 x - + 减 增 所以函数 的递增区间为 ，递减区间为 （3）对任意的 ，使 成立，只需任意的 ，①当 时， 在 上是增函数，所以只需 而 所以 满足题意； ②当 时， ， 在 上是增函数， 所以只需 而 所以 满足题意； ③当 时， ， 在 上是减函数， 上是增函数， 所以只需 即可 而 从而 不满足题意； 综合①②③实数 的取值范围为 .