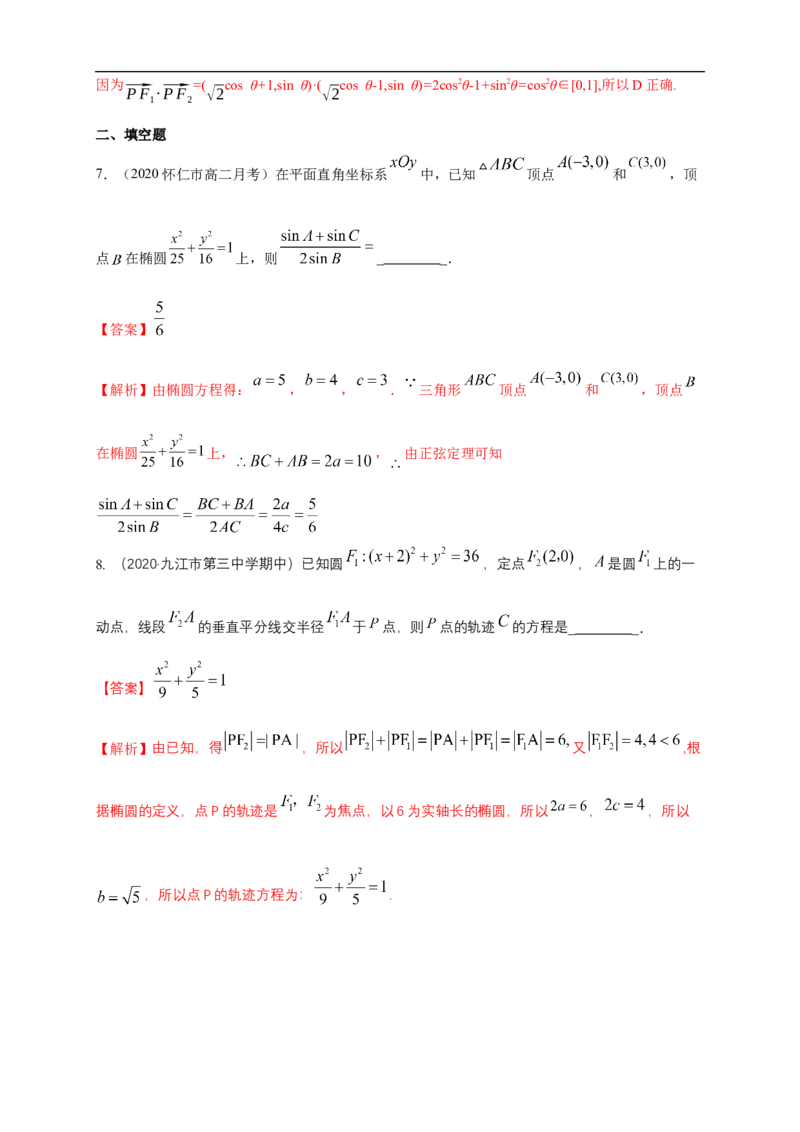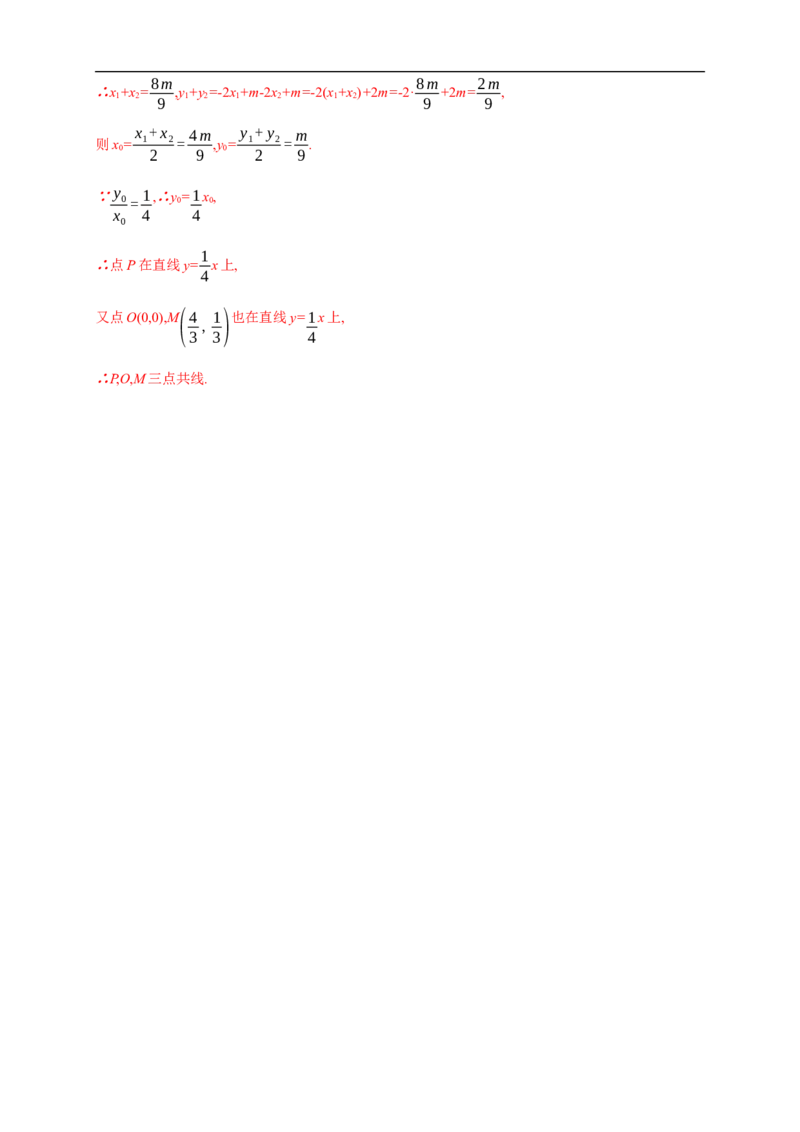文档内容
3.1.1 椭圆的标准方程 -B提高练
一、选择题
1.(2020四川阆中中学)曲线方程 的化简结果为( )
A. B. C. D.
【答案】D
【解析】曲线方程 ,所以其几何意义是动点 到点
和点 的距离之和等于 ,符合椭圆的定义. 点 和点 是椭圆的两个焦点.
因此可得椭圆标准方程 ,其中 ,所以 , ,所以
,所以曲线方程的化简结果为 .故选D项.
x2 y2
2.如果方程 + =1表示焦点在y轴上的椭圆,则m的取值范围是( )
4-m m-3
A.(3,4) B.(7 ) C.( 7) D.(7 )
,+∞ 3, ,4
2 2 2
【答案】D
x2 y2
【解析】因为方程 + =1表示焦点在y轴上的椭圆,所以4-m>0,m-3>0且m-3>4-m,
4-m m-3
7
解得 b>0),
+
a2 b2
{
a2-b2=4,
则 化简并整理得5b4+11b2-16=0,
1 4
+ =1,
a2 5b2
16
故b2=1或b2=- (舍),a2=5,
5
x2
故椭圆M的标准方程为 +y2=1.
5
1 1
(2)由(1)知F(-2,0),F(2,0),设P(x,y),则△PFF 的面积为 ×4×|y |=1,得y=± .
1 2 0 0 1 2 0 0
2 2又x2
0+ y2
=1,所以
x2=
15,x
0
=±√15,
5 0 0 4 2
所以点P有4个,它们的坐标分别为(√15 1) ( √15 1) (√15 1) ( √15 1).
, , - , , ,- , - ,-
2 2 2 2 2 2 2 2
x2 y2 (4 1)
12.如图,椭圆C: + =1(a>b>0)经过点M , ,且点M到椭圆的两焦点的距离之和为2√2.
a2 b2 3 3
(1)求椭圆C的标准方程;
1
(2)若R,S是椭圆C上的两个点,线段RS的中垂线l的斜率为 且直线l与RS交于点P,O为坐标原点,
2
求证:P,O,M三点共线.
【解析】(1)∵点M到椭圆的两焦点的距离之和为2√2,
∴2a=2 ,解得a= .又椭圆C经过点M(4 1),
√2 √2 ,
3 3
(4) 2 (1) 2
∴ =1,解得b2=1.
3 3
+
a2 b2
x2
∴椭圆C的标准方程为 +y2=1.
2
1
(2)∵线段RS的中垂线l的斜率为 ,
2
∴直线RS的斜率为-2,
∴可设直线RS的方程为y=-2x+m.
{y=-2x+m,
联立 得9x2-8mx+2m2-2=0.
x2
+ y2=1,
2
设点R(x,y),S(x,y),P(x,y),
1 1 2 2 0 08m 8m 2m
∴x+x = ,y+y =-2x+m-2x+m=-2(x+x )+2m=-2· +2m= ,
1 2 1 2 1 2 1 2
9 9 9
x +x 4m y + y m
则x= 1 2= ,y= 1 2= .
0 0
2 9 2 9
∵y 1,∴y=1x,
0= 0 0
x 4 4
0
1
∴点P在直线y= x上,
4
又点O(0,0),M(4 1)也在直线y=1x上,
,
3 3 4
∴P,O,M三点共线.