文档内容
3.1.2椭圆的简单几何性质(2) -A基础练
一、选择题
1.(2020·河北桃城衡水中学期末)已知椭圆 ,若长轴长为8,离心率
为 ,则此椭圆的标准方程为( )
A. B. C. D.
【答案】D
【解析】因为椭圆 长轴长为8,所以 ,即 ,
又离心率为 ,所以 ,解得: ,则 = ,
所以椭圆的标准方程为: .
2.(2020全国高二课时练)椭圆有一条光学性质:从椭圆一个焦点出发的光线,经过椭圆反射后,
一定经过另一个焦点.假设光线沿直线传播且在传播过程中不会衰减,椭圆的方程为 ,
则光线从椭圆一个焦点出发,到首次回到该焦点所经过的路程不可能为( )
A.2 B.4 C.6 D.8
【答案】B
【解析】由题意可得 , , ,所以 , .
①若光线从椭圆一个焦点沿 轴方向出发到长轴端点(较近的)再反射,则所经过的路程为
,②若光线从椭圆一个焦点沿 轴方向出发到长轴端点(较远的)再反射,则所经过的路程
为 .③若光线从椭圆一个焦点沿非 轴方向出发,则所经过的路程为 ,故选:B3.(2020·金华市曙光学校月考)无论k为何值,直线 和曲线 交点情况满足
( )
A.没有公共点 B.一个公共点 C.两个公共点 D.有公共点
【答案】D
【解析】因为 过定点 ,且椭圆 的上顶点也为 ,所以当直线的斜
率为 时,此时直线与椭圆相切,仅有一个公共点,当直线的斜率不为零时,此时直线与椭圆有两
个交点,所以无法确定直线与椭圆的公共点是一个还是两个,故选:D.
4. (2019·安徽安庆月考)椭圆 的左焦点为 ,若 关于直线
的对称点 是椭圆 上的点,则椭圆的离心率为( )
A. B. C. D.
【答案】A
【解析】∵点 关于直线 的对称点A为 ,且A在椭圆上,
即 ,∴ ,∴椭圆C的离心率 .
5.(多选题)(2020广东濠江高二月考)椭圆 的焦距为 ,则 的值为( )
A.9 B.23 C. D.
【答案】AB
【解析】椭圆 的焦距为 ,即 得 .依题意当焦点在 轴上时,则,解得 ;当焦点在 轴上时,则 ,解得 ,∴ 的值为9或
23.
6.(多选题)(2020全国高二课时练)嫦娥四号月球探测器于2018年12月8日搭载长征三号乙
运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一
个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为100公里,远月点与月球表
面距离为400公里,已知月球的直径约为3476公里,对该椭圆下述四个结论正确的是( )
A.焦距长约为300公里 B.长轴长约为3988公里
C.两焦点坐标约为 D.离心率约为
【答案】AD
【解析】设该椭圆的半长轴长为 ,半焦距长为 .依题意可得月球半径约为 ,
, , , ,
,椭圆的离心率约为 ,可得结论A、D项正确,B项错
误;
因为没有给坐标系,焦点坐标不确定,所以C项错误.综上可知,正确的为AD,故选:AD.
二、填空题
7. (2020·全国课时练习)若直线 与椭圆 有且只有一个交点,则斜率 的值
是_______.
【答案】【解析】已知直线 与椭圆 有且只有一个交点,由 消去 并整
理,得 ,由题意知, ,解得:
.
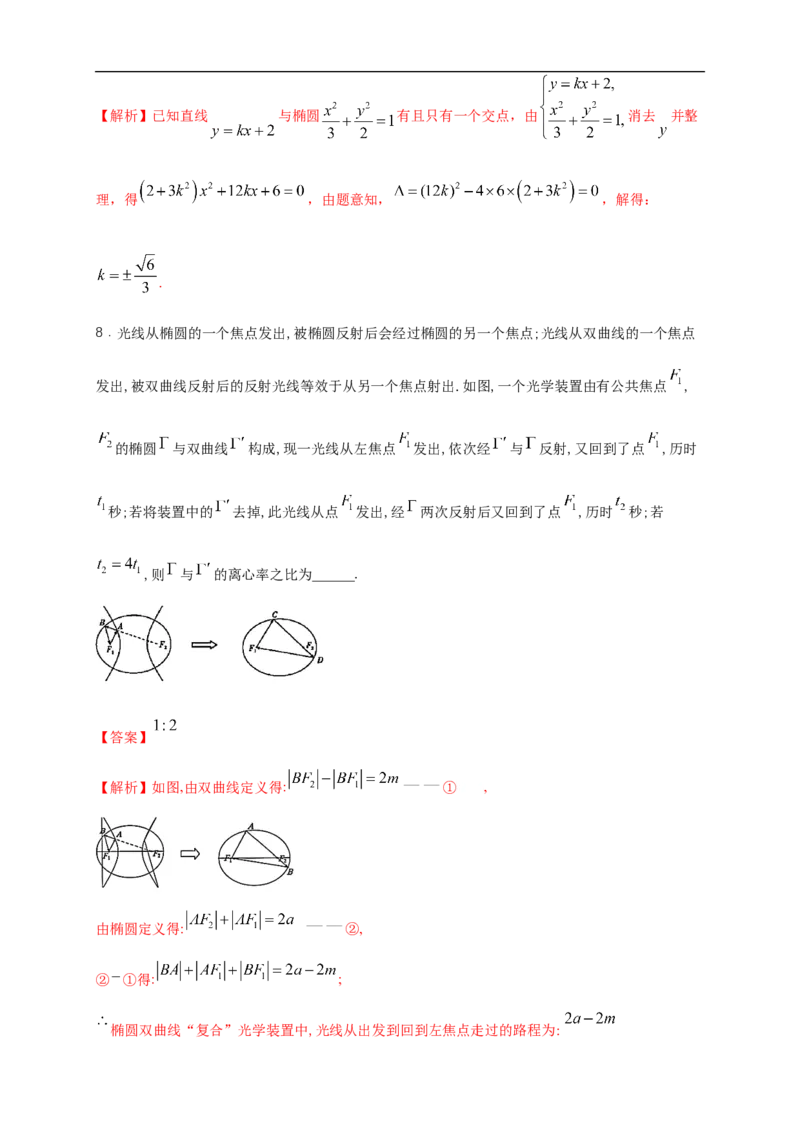
8.光线从椭圆的一个焦点发出,被椭圆反射后会经过椭圆的另一个焦点;光线从双曲线的一个焦点
发出,被双曲线反射后的反射光线等效于从另一个焦点射出.如图,一个光学装置由有公共焦点 ,
的椭圆 与双曲线 构成,现一光线从左焦点 发出,依次经 与 反射,又回到了点 ,历时
秒;若将装置中的 去掉,此光线从点 发出,经 两次反射后又回到了点 ,历时 秒;若
,则 与 的离心率之比为______.
【答案】
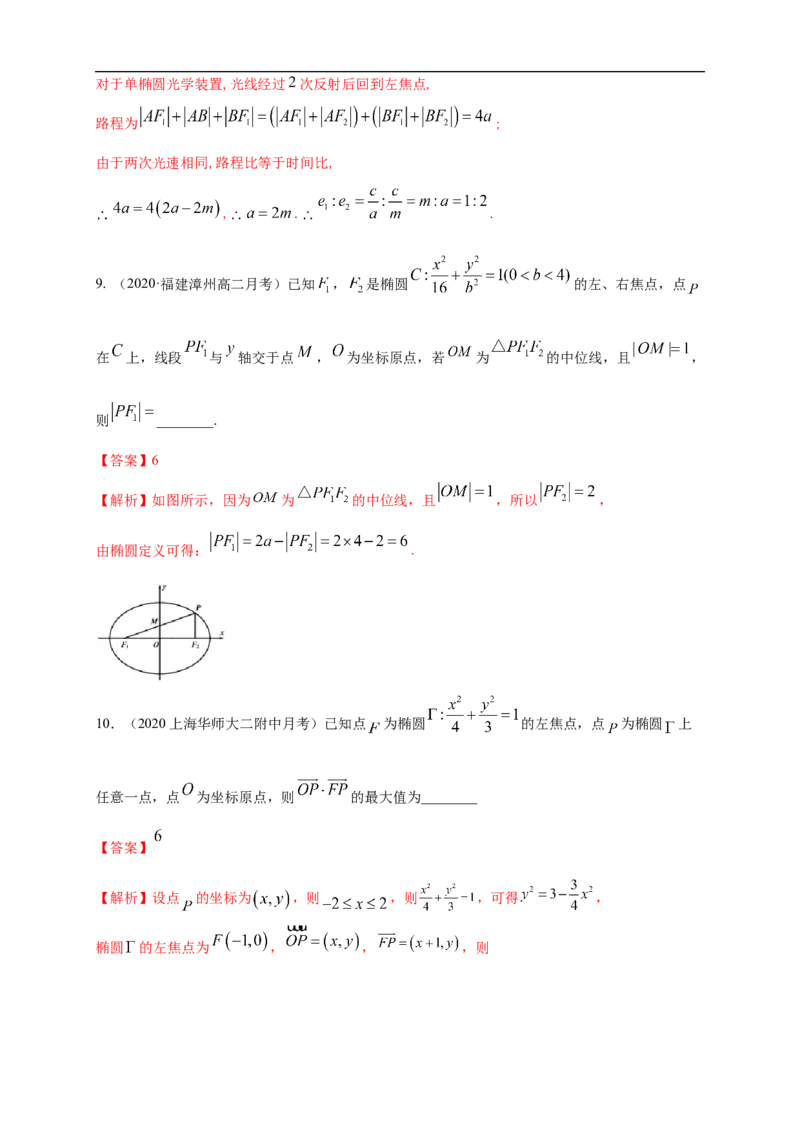
【解析】如图,由双曲线定义得: ① ,
由椭圆定义得: ②,
② ①得: ;
椭圆双曲线“复合”光学装置中,光线从出发到回到左焦点走过的路程为:对于单椭圆光学装置,光线经过 次反射后回到左焦点,
路程为 ;
由于两次光速相同,路程比等于时间比,
, . .
9. (2020·福建漳州高二月考)已知 , 是椭圆 的左、右焦点,点
在 上,线段 与 轴交于点 , 为坐标原点,若 为 的中位线,且 ,
则 ________.
【答案】6
【解析】如图所示,因为 为 的中位线,且 ,所以 ,
由椭圆定义可得: .
10.(2020上海华师大二附中月考)已知点 为椭圆 的左焦点,点 为椭圆 上
任意一点,点 为坐标原点,则 的最大值为________
【答案】
【解析】设点 的坐标为 ,则 ,则 ,可得 ,
椭圆 的左焦点为 , , ,则,
二次函数 在区间 上单调递增,
所以, .因此, 的最大值为 .
三、解答题
11.我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径 )的中心 为
一个焦点的椭圆.如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距
离为 ,远火星点(轨道上离火星表面最远的点) 到火星表面的距离为 .假定
探测器由近火星点 第一次逆时针运行到与轨道中心 的距离为 时进行变轨,其中 分
别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到 ).
【解析】设所求轨道方程为
. .
于是 .所以所求轨道方程为 .
设变轨时,探测器位于 ,则
.解方程组,得 (由题意).
所以探测器在变轨时与火星表面的距离为 .
所以探测器在变轨时与火星表面的距离约为 .
12. (2020全国高二课时练习)已知椭圆C: 经过点 , 是椭
圆 的两个焦点, , 是椭圆 上的一个动点.
(1)求椭圆 的标准方程;
(2)若点 在第一象限,且 ,求点 的横坐标的取值范围;
【解析】(1)由已知得 , ,∴ ,
,同理 ,
∴ , ,∴ ,
椭圆标准方程为 .
(2)设 ( ),
则
, ,∴ ,
∴ ,即 点横坐标取值范围是 .