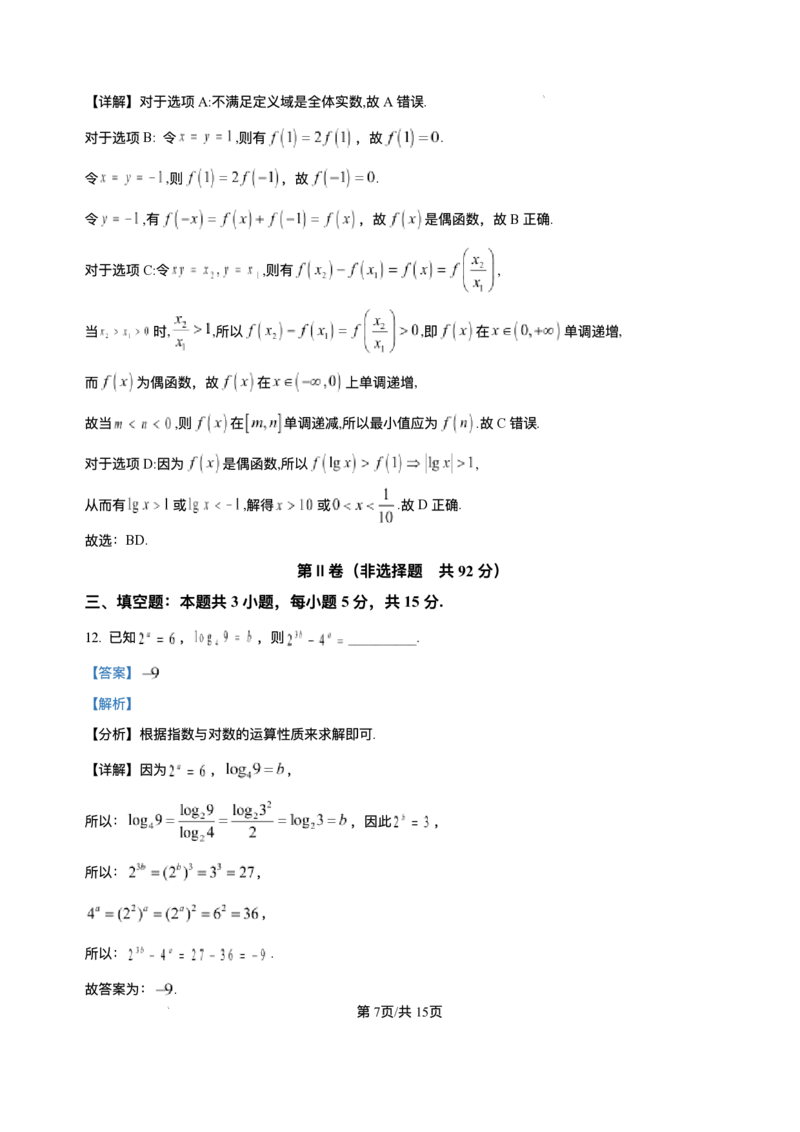文档内容
级⾼⼀ ⽉学情检测
2025 12
数学(⼈教 版)试题
A
本试卷分第I卷(选择题)和第Ⅱ卷(⾮选择题)两部分.满分150分,考试时间120分钟.请
在答题卡上作答.
第I卷(选择题 共58分)
⼀、选择题:本题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项是
符合题⽬要求的.
1. ⻆的终边在( )
A. 第⼀象限 B. 第⼆象限 C. 第三象限 D. 第四象限
2. 已知集合 , ,则 ( )
A. B. C. D.
3. 已知幂函数 在 上单调递增,则 ( )
A.4 B. C. D.4或
4. 已知 是定义在 上的奇函数,当 时, ,则 ( )
A. B. C.1 D.
5. 已知 , , ,则 , , 的⼤⼩关系为( )
A. B. C. D.
6. 已知函数 在 上不具有单调性,则实数 的取值范围是( )
A. B.
C. D.
7.Deepseek(深度求索)是⼈⼯智能的⼀种具有代表性的实现⽅法,它是以神经⽹络为出发点.在神经⽹络
优化中,指数衰减的学习率模型为 ,其中 表示每⼀轮优化时使⽤的学习率, 表示初始学习
率, 表示衰减系数, 表示训练迭代轮数, 表示衰减速度.已知某个指数衰减的学习率模型的初始学
习率为0.8,衰减速度为30,且当训练迭代轮数为10时,学习率衰减为0.4,则学习率衰减到0.3以下(不
第1⻚/共4⻚
学科⽹(北京)股份有限公司含0.3)所需的训练迭代轮数⾄少为( )
(参考数据: , )
A.14 B.15 C.16 D.17
8. 若 ,且 ,则下列不等式⼀定正确 是( )
A. B. C. D.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每个⼩题给出的四个选项中,有多项是
符合题⽬要求.全部选对的得6分,部分选对的得部分分,有选错的得零分.
9. 下列说法正确的是( )
A. 第三象限的⻆⼀定⼤于第⼆象限的⻆
B. 终边在 轴负半轴上的⻆的集合为
C. 若 是第三象限⻆,则 是第⼆或第四象限⻆
D. 函数 的零点是
10. 已知函数 ,则下列结论正确的是( )
A. 当 时, 的单调增区间为
B. 的图象关于直线 对称
C. 若 的定义域为R,则实数 的取值范围
D. 若 的值域为R,则实数 的取值范围
11. 已知定义在实数集上的函数 满⾜ ,且当 时, ,则下列说法
正确的是( )
A. 可以是
B. 是偶函数
C. 在区间 上的最⼩值为
D. 不等式 的解集为
第2⻚/共4⻚
学科⽹(北京)股份有限公司第Ⅱ卷(⾮选择题 共92分)
三、填空题:本题共3⼩题,每⼩题5分,共15分.
12. 已知 , ,则 __________.
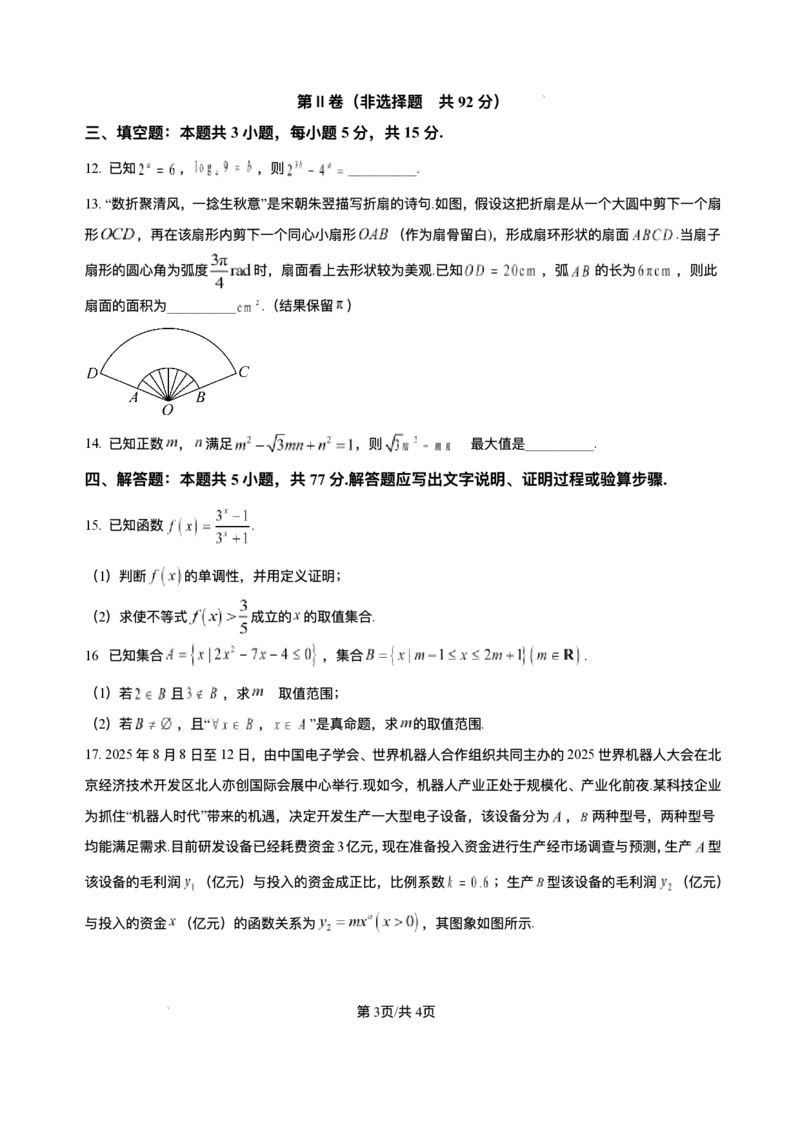
13.“数折聚清⻛,⼀捻⽣秋意”是宋朝朱翌描写折扇的诗句.如图,假设这把折扇是从⼀个⼤圆中剪下⼀个扇
形 ,再在该扇形内剪下⼀个同⼼⼩扇形 (作为扇⻣留⽩),形成扇环形状的扇⾯ .当扇⼦
扇形的圆⼼⻆为弧度 时,扇⾯看上去形状较为美观.已知 ,弧 的⻓为 ,则此
扇⾯的⾯积为__________ .(结果保留 )
14. 已知正数 , 满⾜ ,则 最⼤值是__________.
四、解答题:本题共5⼩题,共77分.解答题应写出⽂字说明、证明过程或验算步骤.
15. 已知函数 .
(1)判断 的单调性,并⽤定义证明;
(2)求使不等式 成⽴的 的取值集合.
16 已知集合 ,集合 .
(1)若 且 ,求 取值范围;
(2)若 ,且“ , ”是真命题,求 的取值范围.
17.2025年8⽉8⽇⾄12⽇,由中国电⼦学会、世界机器⼈合作组织共同主办的2025世界机器⼈⼤会在北
京经济技术开发区北⼈亦创国际会展中⼼举⾏.现如今,机器⼈产业正处于规模化、产业化前夜.某科技企业
为抓住“机器⼈时代”带来的机遇,决定开发⽣产⼀⼤型电⼦设备,该设备分为 , 两种型号,两种型号
均能满⾜需求.⽬前研发设备已经耗费资⾦3亿元,现在准备投⼊资⾦进⾏⽣产经市场调查与预测,⽣产 型
该设备的⽑利润 (亿元)与投⼊的资⾦成正⽐,⽐例系数 ;⽣产 型该设备的⽑利润 (亿元)
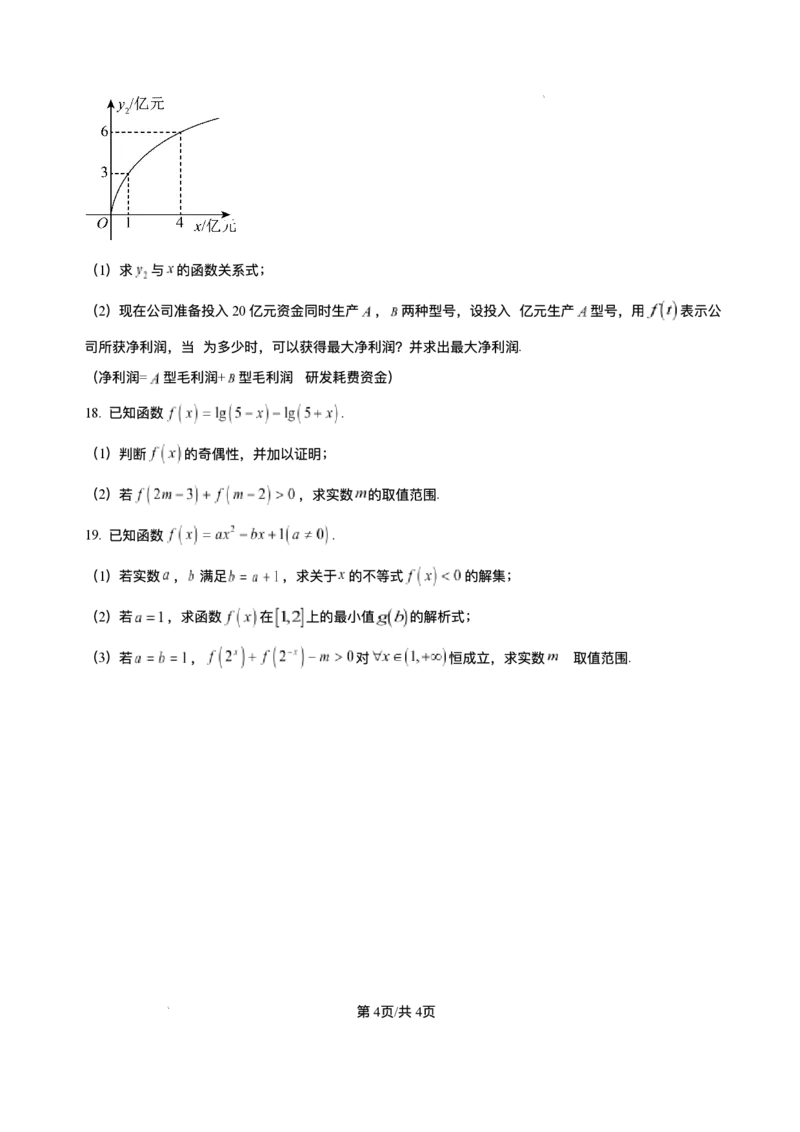
与投⼊的资⾦ (亿元)的函数关系为 ,其图象如图所示.
第3⻚/共4⻚
学科⽹(北京)股份有限公司(1)求 与 的函数关系式;
(2)现在公司准备投⼊20亿元资⾦同时⽣产 , 两种型号,设投⼊ 亿元⽣产 型号,⽤ 表示公
司所获净利润,当 为多少时,可以获得最⼤净利润?并求出最⼤净利润.
(净利润= 型⽑利润+ 型⽑利润 研发耗费资⾦)
18. 已知函数 .
(1)判断 的奇偶性,并加以证明;
(2)若 ,求实数 的取值范围.
19. 已知函数 .
(1)若实数 , 满⾜ ,求关于 的不等式 的解集;
(2)若 ,求函数 在 上的最⼩值 的解析式;
(3)若 , 对 恒成⽴,求实数 取值范围.
第4⻚/共4⻚
学科⽹(北京)股份有限公司级⾼⼀ ⽉学情检测
2025 12
数学(⼈教 版)试题
A
本试卷分第I卷(选择题)和第Ⅱ卷(⾮选择题)两部分.满分150分,考试时间120分钟.请
在答题卡上作答.
第I卷(选择题 共58分)
⼀、选择题:本题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项是
符合题⽬要求的.
1. ⻆的终边在( )
A. 第⼀象限 B. 第⼆象限 C. 第三象限 D. 第四象限
【答案】C
【解析】
【分析】把 变成0到360度内的⻆即可判断.
【详解】因为 ,所以 ⻆的终边在第三象限.
故选:C.
2. 已知集合 , ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】根据对数型复合函数定义域、绝对值不等式的求法可分别求得集合 ,由交集定义可得结果.
【详解】 ,
,
,即 .
故选:B.
3. 已知幂函数 在 上单调递增,则 ( )
A.4 B. C. D.4或
【答案】A
第1⻚/共15⻚
学科⽹(北京)股份有限公司【解析】
【分析】根据幂函数的定义结合单调性分析求解即可.
【详解】因为函数 是幂函数,
则 ,解得 或 ,
⼜因为幂函数 在 上单调递增,则
所以 .
故选:A.
4. 已知 是定义在 上的奇函数,当 时, ,则 ( )
A. B. C.1 D.
【答案】D
【解析】
【分析】由条件可知 ,代⼊指定解析式得 ,
【详解】 是定义在 上的奇函数, , 时, ,
所以 , .
故选:D
5. 已知 , , ,则 , , 的⼤⼩关系为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据对数以及指数的单调性即可求解.
【详解】由于 , , ,
故 ,
第2⻚/共15⻚
学科⽹(北京)股份有限公司故选:D
6. 已知函数 在 上不具有单调性,则实数 的取值范围是( )
A. B.
C. D.
【答案】B
【解析】
【分析】本题函数为⼆次函数,在 上不具有单调性,则对称轴在区间中间,列不等式进⾏求解.
【详解】函数 图象的对称轴为 ,
因为函数 在区间 上不具有单调性,
所以 ,解得 .
故实数 的取值范围为 .
故选:B.
7.Deepseek(深度求索)是⼈⼯智能的⼀种具有代表性的实现⽅法,它是以神经⽹络为出发点.在神经⽹络
优化中,指数衰减的学习率模型为 ,其中 表示每⼀轮优化时使⽤的学习率, 表示初始学习
率, 表示衰减系数, 表示训练迭代轮数, 表示衰减速度.已知某个指数衰减的学习率模型的初始学
习率为0.8,衰减速度为30,且当训练迭代轮数为10时,学习率衰减为0.4,则学习率衰减到0.3以下(不
含0.3)所需的训练迭代轮数⾄少为( )
(参考数据: , )
A.14 B.15 C.16 D.17
【答案】B
【解析】
【分析】根据已知条件列⽅程,可得 ,再由 ,结合指对数关系和对数函数的性
质求解即可.
【详解】由于 ,所以 ,
第3⻚/共15⻚
学科⽹(北京)股份有限公司依题意 ,则 ,
则 ,由 ,
两边同时取对数可得 , , ,
,
即 ,所以所需的训练迭代轮数⾄少为15次.
故选:B
8. 若 ,且 ,则下列不等式⼀定正确的是( )
A. B. C. D.
【答案】A
【解析】
【分析】令 ,得到 为递减函数,化简得到 和
,转换为 ,转化为 ,结合 的单调
性,即可求解.
【详解】令 ,因为 和 在 上都是递减函数,
所以 在 上是递减函数,
⼜由 ,
因为
⼜因为 ,则 ,所以 ,
因为 ,所以 ,即
因为 在 上是递减函数,可得 ,所以⼀定成⽴的是 .
故选:A.
⼆、选择题:本题共3⼩题,每⼩题6分,共18分.在每个⼩题给出的四个选项中,有多项是
符合题⽬要求.全部选对的得6分,部分选对的得部分分,有选错的得零分.
第4⻚/共15⻚
学科⽹(北京)股份有限公司9. 下列说法正确的是( )
A. 第三象限的⻆⼀定⼤于第⼆象限的⻆
B. 终边在 轴负半轴上的⻆的集合为
C. 若 是第三象限⻆,则 是第⼆或第四象限⻆
D. 函数 的零点是
【答案】BC
【解析】
【分析】利⽤赋值法可判断A;根据⻆的终边可直接得到⻆的集合,判断B选项;根据象限⻆的范围求得
的范围,结合象限⻆的范围判断C选项;求得函数的零点判断D选项.
【详解】对于A, 是第三象限⻆, 是第⼆象限⻆,但 ,故A错误;
对于B,终边在 轴负半轴上的⻆的集合为 ,故B正确;
对于C,若 是第三象限⻆,则 ,则 ,
当 时, ,所以 是第四象限⻆,
当 时, ,所以 是第⼆象限⻆,故C选项正确;
对于D,令 ,得 ,解得 ,
所以函数 零点是 .故D选项错误.
故选:BC.
10. 已知函数 ,则下列结论正确的是( )
A. 当 时, 的单调增区间为
B. 的图象关于直线 对称
C. 若 的定义域为R,则实数 的取值范围
D. 若 的值域为R,则实数 的取值范围
第5⻚/共15⻚
学科⽹(北京)股份有限公司【答案】ABC
【解析】
【分析】利⽤复合函数的单调性可判定A项,利⽤抽象函数的对称性性质可判定B项,根据⼆次函数恒能
成⽴可判定C、D项
【详解】对于A项,当 时, ,
令 得 或 ,
⽽由⼆次函数的单调性可知 的单调递增区间为 ,
根据复合函数同增异减的性质知 的单调增区间为 ,故A正确;
对于B项,易知 ,
所以 的图象关于直线 对称,故B正确;
对于C项,若 的定义域为R,则 在R上恒成⽴,
所以 ,即 ,故C正确;
对于D项,若 的值域为R,则 在R上有解,即 ,
解得 ,故D错误.
故选:ABC
11. 已知定义在实数集上的函数 满⾜ ,且当 时, ,则下列说法
正确的是( )
A. 可以是
B. 是偶函数
C. 在区间 上的最⼩值为
D. 不等式 的解集为
【答案】BD
【解析】
【分析】根据定义域判断A,利⽤赋值法结合偶函数的定义判断B正确.判断出函数的单调性后可判断C错
误,根据单调性和偶函数结合对数函数的单调性求出不等式的解后判断D.
第6⻚/共15⻚
学科⽹(北京)股份有限公司【详解】对于选项A:不满⾜定义域是全体实数,故A错误.
对于选项B: 令 ,则有 ,故 .
令 ,则 ,故 .
令 ,有 ,故 是偶函数,故B正确.
对于选项C:令 ,则有 ,
当 时, ,所以 ,即 在 单调递增,
⽽ 为偶函数,故 在 上单调递增,
故当 ,则 在 单调递减,所以最⼩值应为 .故C错误.
对于选项D:因为 是偶函数,所以 ,
从⽽有 或 ,解得 或 .故D正确.
故选:BD.
第Ⅱ卷(⾮选择题 共92分)
三、填空题:本题共3⼩题,每⼩题5分,共15分.
12. 已知 , ,则 __________.
【答案】
【解析】
【分析】根据指数与对数的运算性质来求解即可.
【详解】因为 , ,
所以: ,因此 ,
所以: ,
,
所以: .
故答案为: .
第7⻚/共15⻚
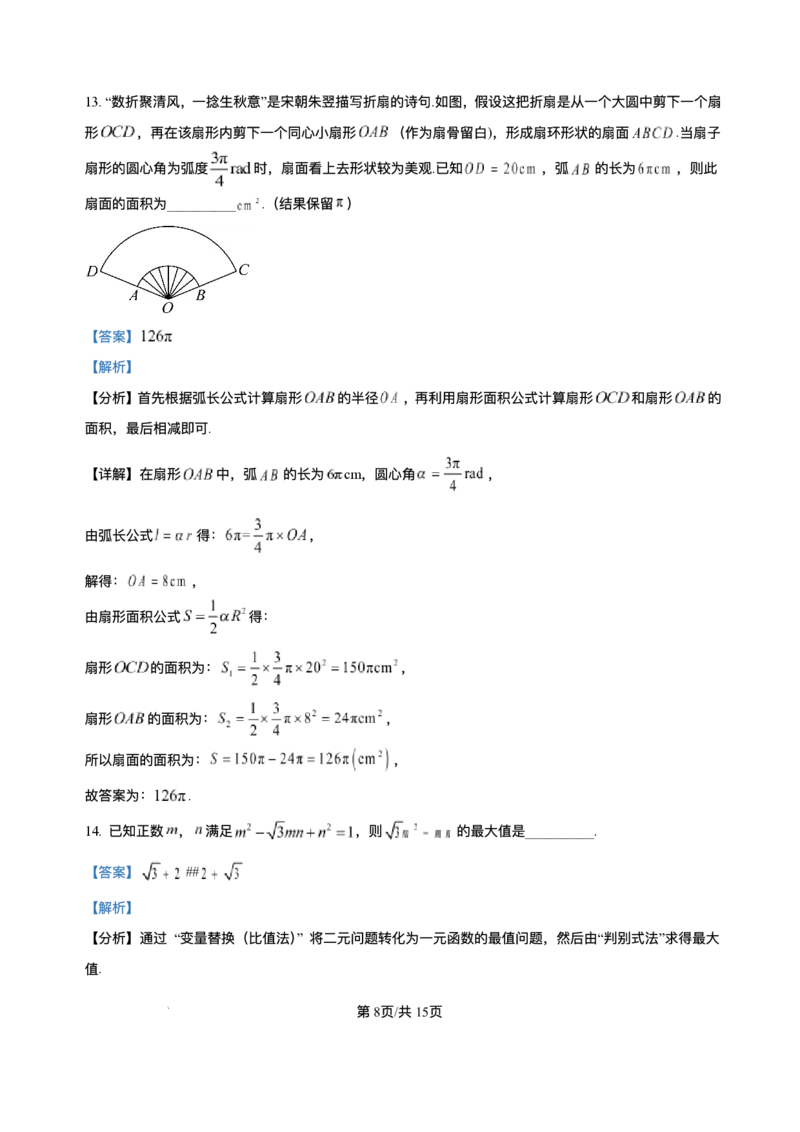
学科⽹(北京)股份有限公司13.“数折聚清⻛,⼀捻⽣秋意”是宋朝朱翌描写折扇的诗句.如图,假设这把折扇是从⼀个⼤圆中剪下⼀个扇
形 ,再在该扇形内剪下⼀个同⼼⼩扇形 (作为扇⻣留⽩),形成扇环形状的扇⾯ .当扇⼦
扇形的圆⼼⻆为弧度 时,扇⾯看上去形状较为美观.已知 ,弧 的⻓为 ,则此
扇⾯的⾯积为__________ .(结果保留 )
【答案】
【解析】
【分析】⾸先根据弧⻓公式计算扇形 的半径 ,再利⽤扇形⾯积公式计算扇形 和扇形 的
⾯积,最后相减即可.
【详解】在扇形 中,弧 的⻓为 cm,圆⼼⻆ ,
由弧⻓公式 得: ,
解得: ,
由扇形⾯积公式 得:
扇形 的⾯积为: ,
扇形 的⾯积为: ,
所以扇⾯的⾯积为: ,
故答案为: .
14. 已知正数 , 满⾜ ,则 的最⼤值是__________.
【答案】 ##
【解析】
【分析】通过 “变量替换(⽐值法)” 将⼆元问题转化为⼀元函数的最值问题,然后由“判别式法”求得最⼤
值.
第8⻚/共15⻚
学科⽹(北京)股份有限公司【详解】设 ,即 ,
则 ,
∵关于 的⼆次三项式 的判别式 ,即 恒成⽴,
∴ ,
则 , ,
∴ ,
令 ,则 ,⽅程⼀定存在正根,
则 ,
即 ,解得 ,
当 时,⽅程整理为 即 ,符合题意,
∴ 的最⼤值为 .
故答案为: .
四、解答题:本题共5⼩题,共77分.解答题应写出⽂字说明、证明过程或验算步骤.
15. 已知函数 .
(1)判断 的单调性,并⽤定义证明;
(2)求使不等式 成⽴的 的取值集合.
【答案】(1)函数 单调递增,证明⻅解析.
(2)
【解析】
【分析】(1)根据函数单调性的定义进⾏证明即可.
第9⻚/共15⻚
学科⽹(北京)股份有限公司(2)先求出 解,然后根据函数的单调性求出不等式的解集即可.
【⼩问1详解】
函数 单调递增,证明:
设 ,则 .
因为 ,所以 ,所以 .
所以函数 单调递增.
⼩问2详解】
令 ,则 ,化简得 ,解得 .
由(1)知函数 单调递增,所以要使得不等式 成⽴,
则 ,所以使不等式 成⽴的 的取值集合为 .
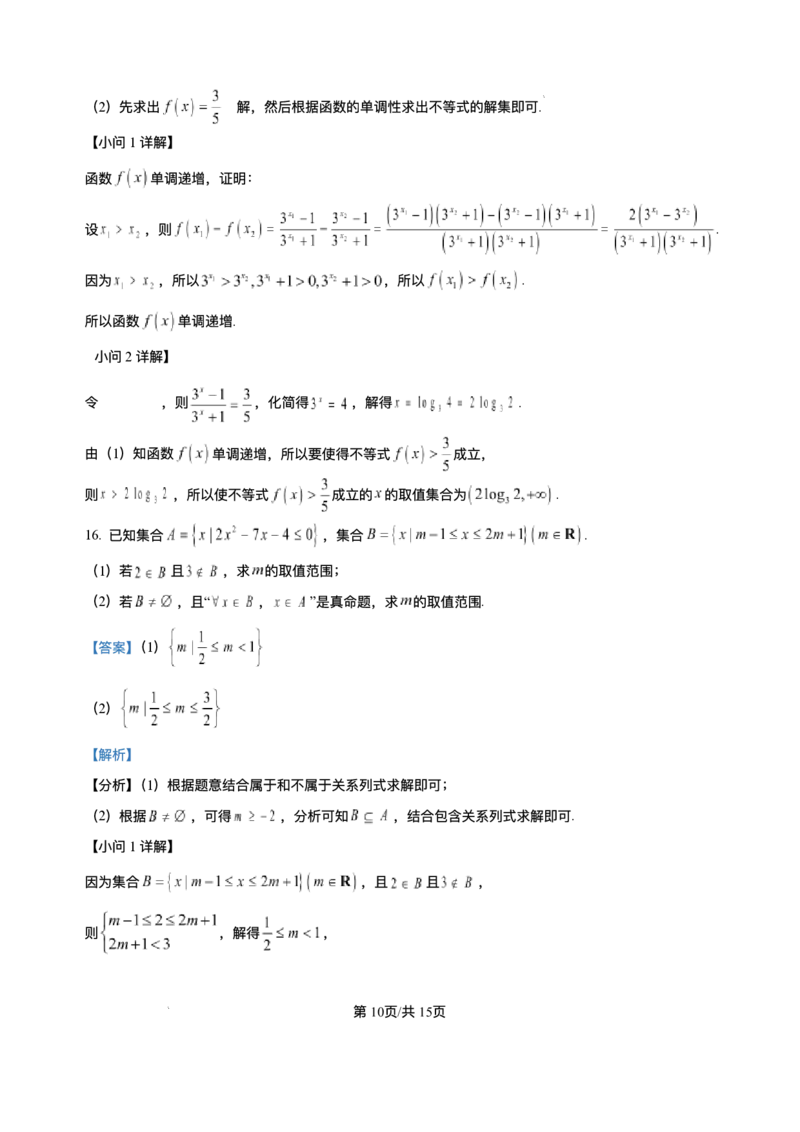
16. 已知集合 ,集合 .
(1)若 且 ,求 的取值范围;
(2)若 ,且“ , ”是真命题,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据题意结合属于和不属于关系列式求解即可;
(2)根据 ,可得 ,分析可知 ,结合包含关系列式求解即可.
【⼩问1详解】
因为集合 ,且 且 ,
则 ,解得 ,
第10⻚/共15⻚
学科⽹(北京)股份有限公司所以 的取值范围为 .
【⼩问2详解】
由题意可知:集合 ,
因为 ,则 ,解得 ,
⼜因为“ , ”是真命题,可知 ,
则 ,解得 ,
所以 的取值范围为 .
17.2025年8⽉8⽇⾄12⽇,由中国电⼦学会、世界机器⼈合作组织共同主办的2025世界机器⼈⼤会在北
京经济技术开发区北⼈亦创国际会展中⼼举⾏.现如今,机器⼈产业正处于规模化、产业化前夜.某科技企业
为抓住“机器⼈时代”带来的机遇,决定开发⽣产⼀⼤型电⼦设备,该设备分为 , 两种型号,两种型号
均能满⾜需求.⽬前研发设备已经耗费资⾦3亿元,现在准备投⼊资⾦进⾏⽣产经市场调查与预测,⽣产 型
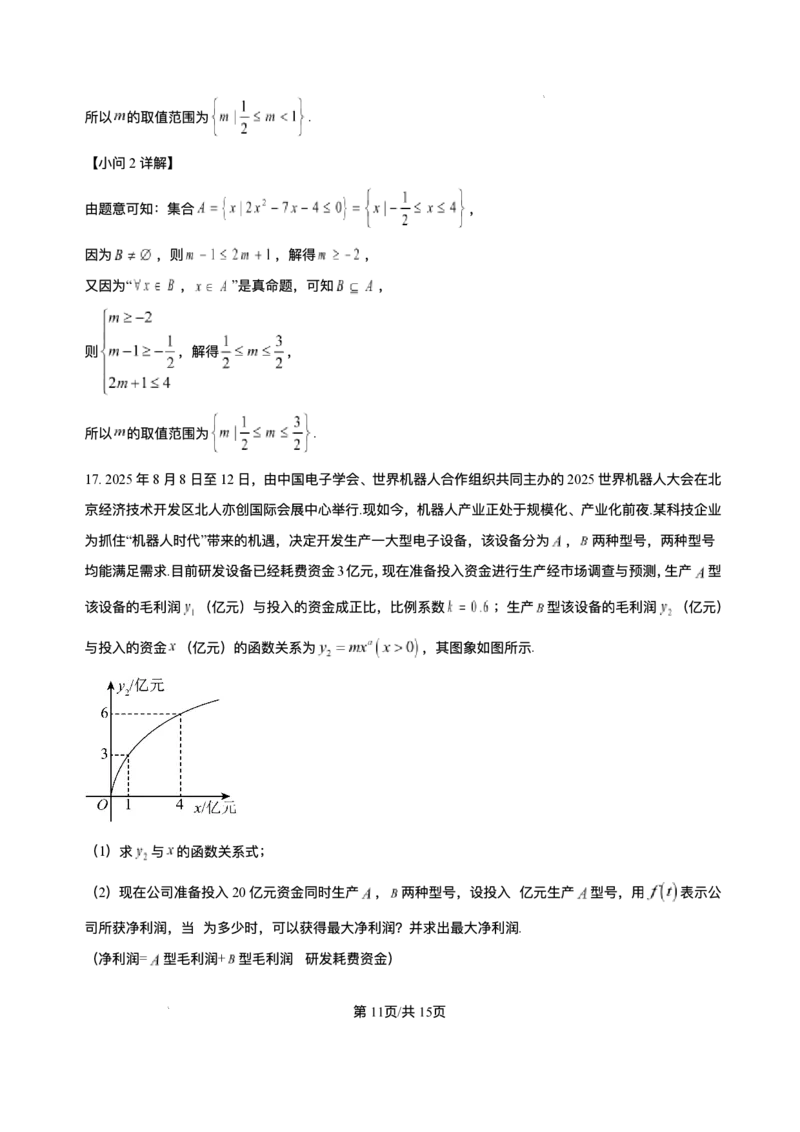
该设备的⽑利润 (亿元)与投⼊的资⾦成正⽐,⽐例系数 ;⽣产 型该设备的⽑利润 (亿元)
与投⼊的资⾦ (亿元)的函数关系为 ,其图象如图所示.
(1)求 与 的函数关系式;
(2)现在公司准备投⼊20亿元资⾦同时⽣产 , 两种型号,设投⼊ 亿元⽣产 型号,⽤ 表示公
司所获净利润,当 为多少时,可以获得最⼤净利润?并求出最⼤净利润.
(净利润= 型⽑利润+ 型⽑利润 研发耗费资⾦)
第11⻚/共15⻚
学科⽹(北京)股份有限公司【答案】(1)
(2) 时,可以获得最⼤净利润 亿元.
【解析】
【分析】(1)由函数图象知图象经过的点坐标,将点坐标代⼊函数解析式,即可求得参数,即可求得解析
式;
(2)由题意写出 与 的函数关系式,由净利润公式写出表达式,通过换元将函数转变为⼆次函数,由⼆
次函数的对称轴求得最⼤值;
【⼩问1详解】
由函数图象可知,函数图象经过 ,
∴ ,解得 ,
∴
【⼩问2详解】
由题意可知 ,
则 ,
设 ,则 ,
∴函数 ,
函数 开⼝向下,且对称轴为 ,
则 ,
当 ,即 时,函数 取最⼤值 .
即当投⼊ 亿元⽣产 型号时,可以获得最⼤净利润 亿元.
18. 已知函数 .
(1)判断 的奇偶性,并加以证明;
第12⻚/共15⻚
学科⽹(北京)股份有限公司(2)若 ,求实数 的取值范围.
【答案】(1)奇函数,证明⻅解析
(2)
【解析】
【分析】(1)根据函数的奇偶性定义进⾏解答即可.
(2)将不等式进⾏化简,根据对数函数 性质求出解集即可.
⼩问1详解】
为奇函数.证明:
要使函数 有意义,则 ,解得 .
所以 的定义域为 ,关于原点对称.
⽽ ,所以 为奇函数.
【⼩问2详解】
由(1)知 为奇函数,所以 .
由 可得 .
函数 在 上都意识递减,
则 在定义域 上是减函数,所以需满⾜ ,
解得 .
19. 已知函数 .
(1)若实数 , 满⾜ ,求关于 的不等式 的解集;
(2)若 ,求函数 在 上的最⼩值 的解析式;
(3)若 , 对 恒成⽴,求实数 的取值范围.
【答案】(1)答案⻅解析;
第13⻚/共15⻚
学科⽹(北京)股份有限公司(2) ;
(3)
【解析】
【分析】(1)含参数分类讨论解不等式计算即可;
(2)利⽤⼆次函数的性质,分类讨论b的范围计算即可;
(3)根据指数函数、⼆次函数、对勾函数的单调性结合换元法计算即可.
【⼩问1详解】
由 得 ,
若 ,则 ;
若 ,则不等式解集为 ;
若 ,则不等式解集为 ;
若 ,则不等式解集为 或 ;
综上所述: 时,不等式解集为 , 时,不等式解集为 ,
时,不等式解集为 , 时,不等式解集为 或 ;
【⼩问2详解】
若 ,即 ,
易知 在 上单调递增,在 上单调递减,
若 ,即 时,则 ,
第14⻚/共15⻚
学科⽹(北京)股份有限公司若 ,即 时,则 ,
若 ,即 时,则 ,
综上 ;
【⼩问3详解】
若 ,即 ,
所以 ,
令 ,易知 时, ,设 ,
由对勾函数的性质知 在 上单调递增,所以 ,
故 对 恒成⽴等价于
对 恒成⽴,
由⼆次函数的性质可知 ,所以 ,
即
第15⻚/共15⻚
学科⽹(北京)股份有限公司