文档内容
格致课堂
6.3.1 平面向量基本定理
(用时45分钟)
【选题明细表】
知识点、方法 题号
基底的概念及辨析 1,2,10
用基底表示向量 3,5,6,7,9
平面向量基本定理的应用 4,8,11,12
基础巩固
1.如果 是平面 内两个不共线的向量,那么在下列各命题中不正确的有()
① 可以表示平面 内的所有向量;②对于平面 内的任一向量 ,使
的实数 ,有无数多对;③若向量 与 共线,则有且只有一个实数 ,使
;④若实数 ,使 ,则 .
A.①② B.②③
C.③④ D.②
【答案】B
【解析】由平面向量基本定理可知,①是正确的;
对于②,由平面向量基本定理可知,一个平面的基底确定,那么任意一个向量在此基底下的实数对是唯一
的;
对于③,当两向量的系数均为零即 时,这样的 有无数个;
对于④,若 ,则 ,由平面向量共线定理知, 共线,与题意矛盾,故 ,
即有 ,因此 ;
故选B.格致课堂
2.已知向量 , 不共线,实数x,y满 ,则 的值是( )
A.3 B. C.0 D.2
【答案】A
【解析】
由题意得 解得 .
故选:A
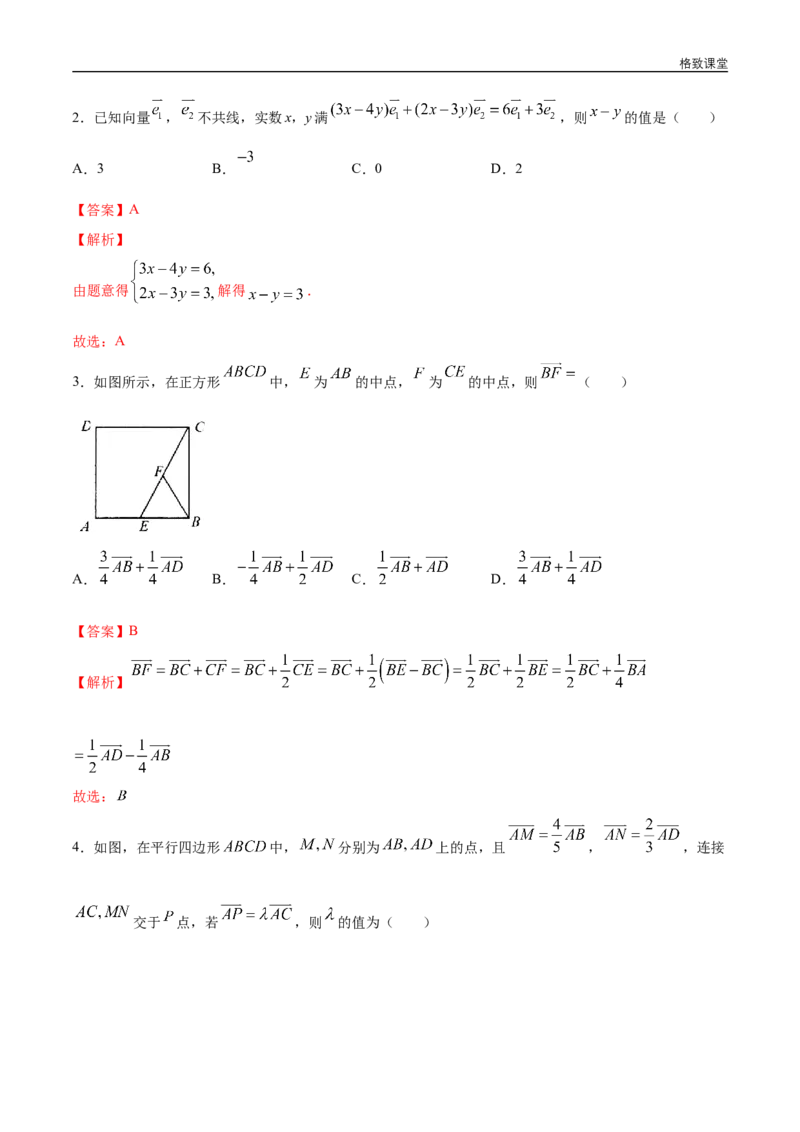
3.如图所示,在正方形 中, 为 的中点, 为 的中点,则 ( )
A. B. C. D.
【答案】B
【解析】
故选:
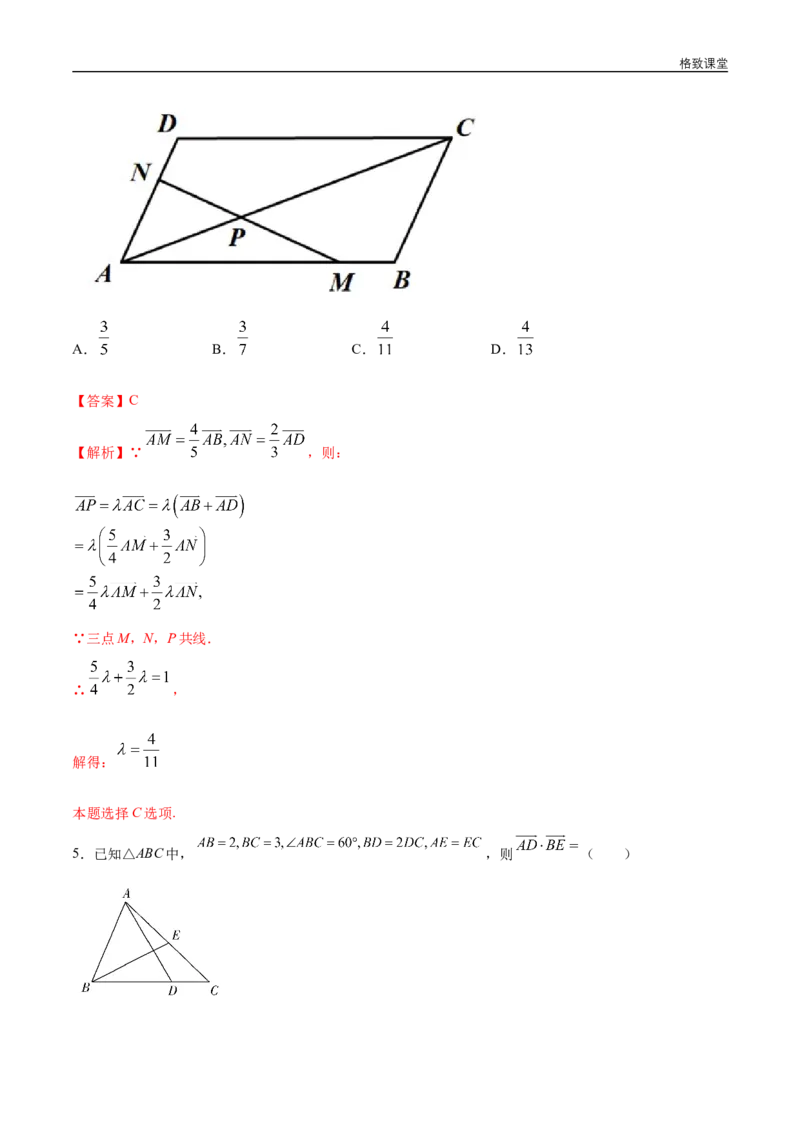
4.如图,在平行四边形 中, 分别为 上的点,且 , ,连接
交于 点,若 ,则 的值为( )格致课堂
A. B. C. D.
【答案】C
【解析】∵ ,则:
∵三点M,N,P共线.
∴ ,
解得:
本题选择C选项.
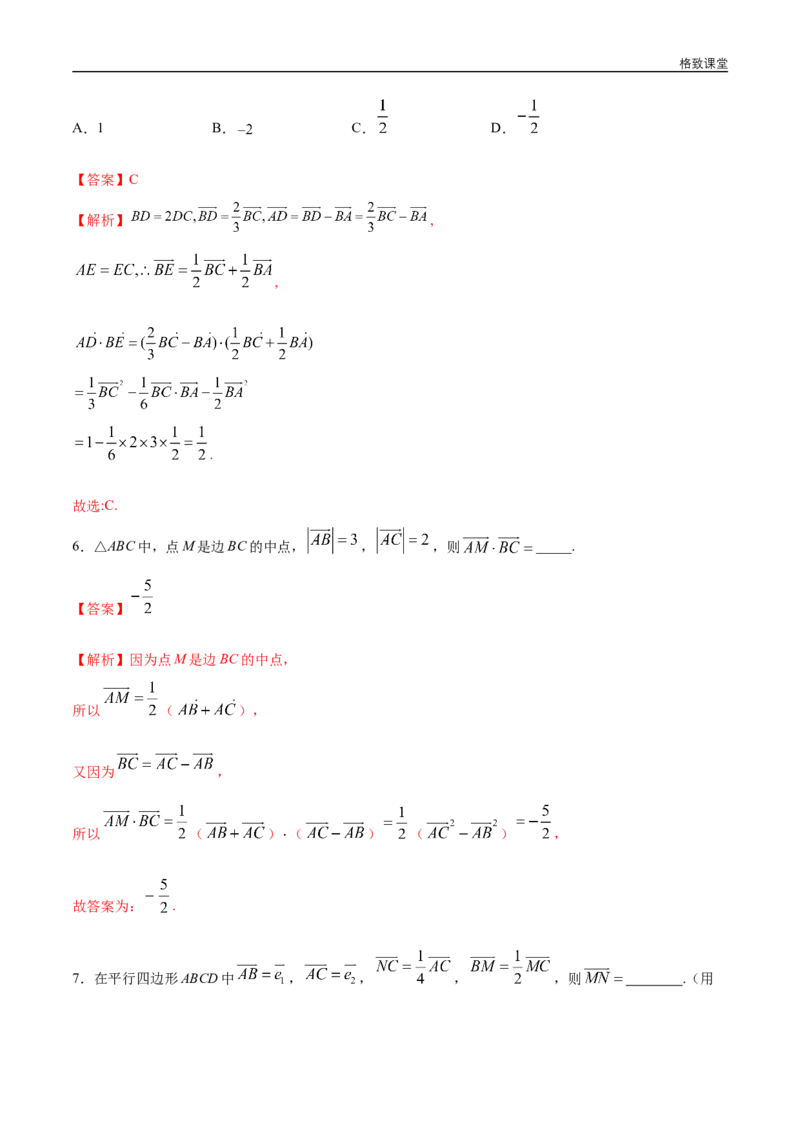
5.已知△ABC中, ,则 ( )格致课堂
A.1 B. C. D.
【答案】C
【解析】 ,
,
.
故选:C.
6.△ABC中,点M是边BC的中点, , ,则 _____.
【答案】
【解析】因为点M是边BC的中点,
所以 ( ),
又因为 ,
所以 ( ) ( ) ( ) ,
故答案为: .
7.在平行四边形ABCD中 , , , ,则 .(用格致课堂
表示)
【答案】
【解析】如图:
= -
= +2 = +
=- + ( - )
=- +
= .
故本题答案为 .
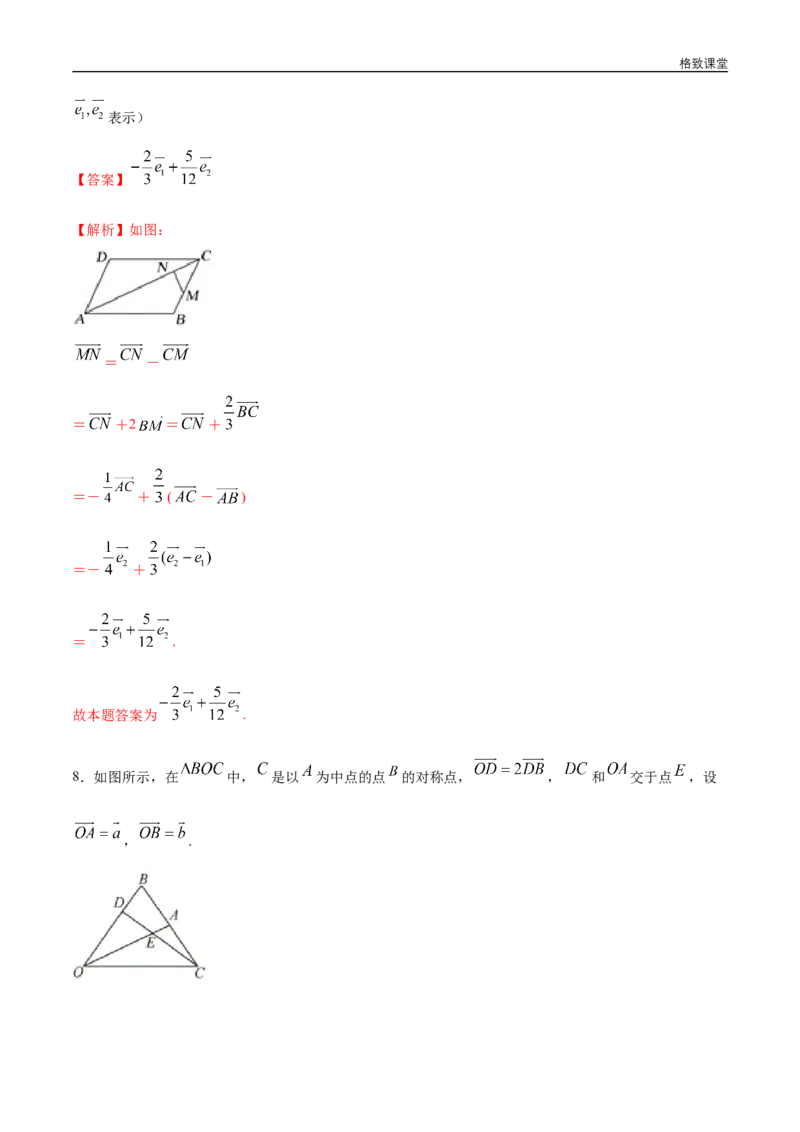
8.如图所示,在 中, 是以 为中点的点 的对称点, , 和 交于点 ,设
, .格致课堂
(1)用 和 表示向量 、 ;
(2)若 ,求实数 的值.
【答案】(1) , ;(2) .
【解析】(1)由题意知, 是线段 中点,且 .
,
;
(2) ,
由题可得 ,且 ,
设 ,即 ,则有 ,解得 .
因此, .
能力提升
9.在 中,点F为线段BC上任一点(不含端点),若 ,则
的最小值为( )
A.1 B.8 C.2 D.4
【答案】B格致课堂
【解析】因为 ,且点F在线段BC上,
则 ,且 ,
则 .
故选:B.
10.设向量 , , ,用 、 表示 ,则 ______.
【答案】
【解析】设 ,则 ,
得 ,解得 ,所以 .
故答案为: .
11.已知 为两个不共线的向量,若四边形 满足 ,
(1)将⃗AD用 表示;
(2)证明四边形 为梯形.
【答案】(1) (2)详见解析
【解析】(1)格致课堂
(2)因为 ,即 ,
所以 与 同方向,且 的长度为 的长度的2倍,
所以在四边形 中, ,且 ,
所以四边形 是梯形.
素养达成
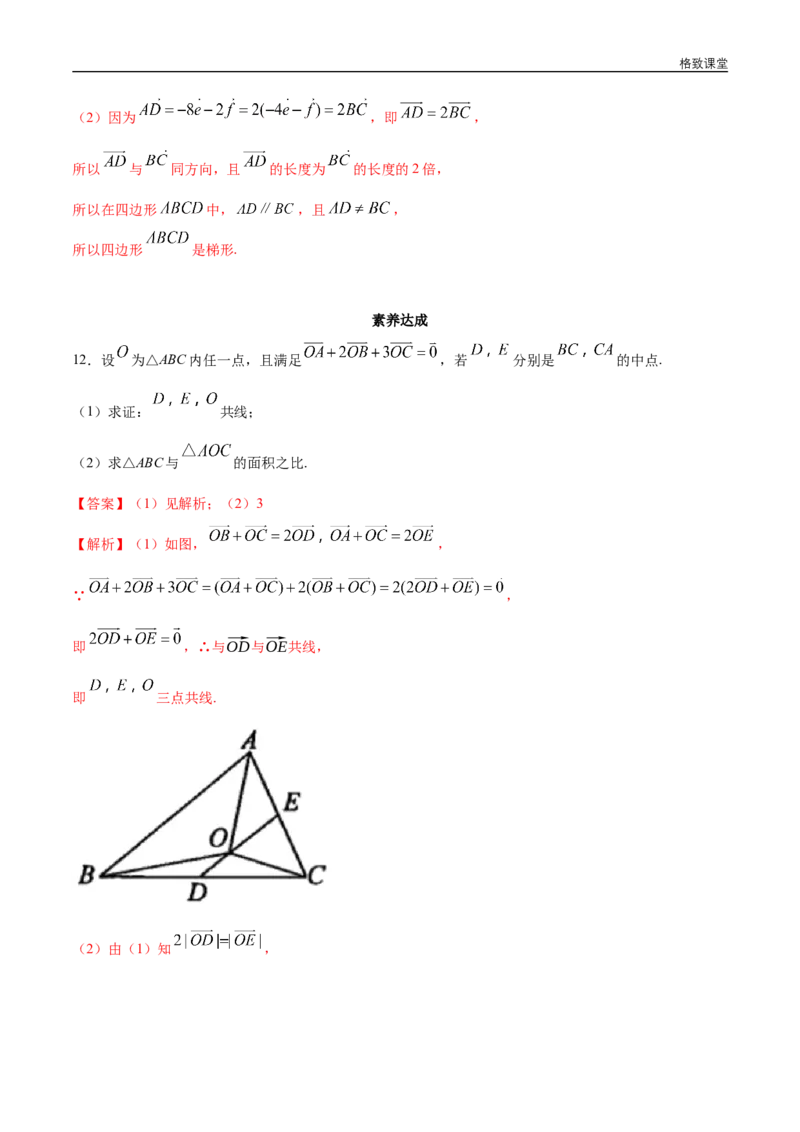
12.设 为△ABC内任一点,且满足 ,若 分别是 的中点.
(1)求证: 共线;
(2)求△ABC与 的面积之比.
【答案】(1)见解析;(2)3
【解析】(1)如图, ,
∵ ,
即 ,∴与⃗OD与⃗OE共线,
即 三点共线.
(2)由(1)知 ,格致课堂
∴ ,
∴ .