文档内容
格致课堂
6.3.1 平面向量基本定理
一、选择题
1.(2019·全国高一课时练习)下面三种说法,其中正确的是( )
①一个平面内只有一对不共线向量可作为表示该平面的基底;
②一个平面内有无数多对不共线向量可作为该平面所有向量的基底;
③零向量不可以作为基底中的向量.
A.①② B.②③ C.①③ D.①②③
【答案】B
【解析】由题意知,说法①中,只要是不共线的一对向量就可以作为该平面的基底,故说法①错;
则②③显然正确,故选B.
2.已知向量 ,且 , , ,则一定共线的三点是(
)
A. B. C. D.
【答案】A
【解析】由题意,向量 ,且 , , ,
可得 ,即 共线,所以 三点共线,
故选A.。
3.(2019·全国高一课时练习)在 中, , .若点 满足 ,则
( )
A. B. C. D.
【答案】A
【解析】 ,故选A.
4.(2019·全国高一课时练习)已知向量 不共线,若向量 与 的方向相反,则
等于( )格致课堂
A.1 B.0 C. D.
【答案】C
【解析】∵向量 与 的方向相反,∴ .
由向量共线的性质定理可知,存在一个实数 ,使得 ,
即 ,解得 .
当 时,向量 与 是相等向量,其方向相同,不符合题意,故舍去;
∴ .
故选C。
5.(多选题)(2019·全国高一课时练习)已知非零向量 , 满足
,给出以下结论,其中正确结论是( )
A.若 与 不共线, 与 共线,则 ;
B.若 与 不共线, 与 共线,则 ;
C.存在实数 ,使得 与 不共线, 与 共线;
D.不存在实数 ,使得 与 不共线, 与 共线
【答案】AD
【解析】因为非零向量 , 满足 ,
若 与 不共线, 与 共线,可得 ,即 , ,解得 ,所以A正确,
B错误.
若 与 共线,可得 ,可得 与
共线,所以C错误,D正确.故选AD。
6.(多选题)(2019·全国高一课时练习)已知向量 是两个非零向量,在下列四个条件中,一格致课堂
定能使 共线的是( )
A. 且 ;
B.存在相异实数入 ,使 ;
C. (其中实数 满足 );
D.已知梯形 ,其中 。
【答案】AB
【解析】A由 得 ,所以 ,故A正确;
B因为存在相异实数入 ,使 ;所以 ,所以 ,故B正确;
C若 ,则 ,但 不一定共线,故C错误;
D梯形 中,没有说明哪组对边平行,故D错误.
故选AB。
二、填空题
7.(2019·全国高一课时练习)设向量 与 不共线,若 , ,
,且 三点共线,则 _______.
【答案】
【解析】
三点共线且向量 与 不共线
,解得:
本题正确结果:
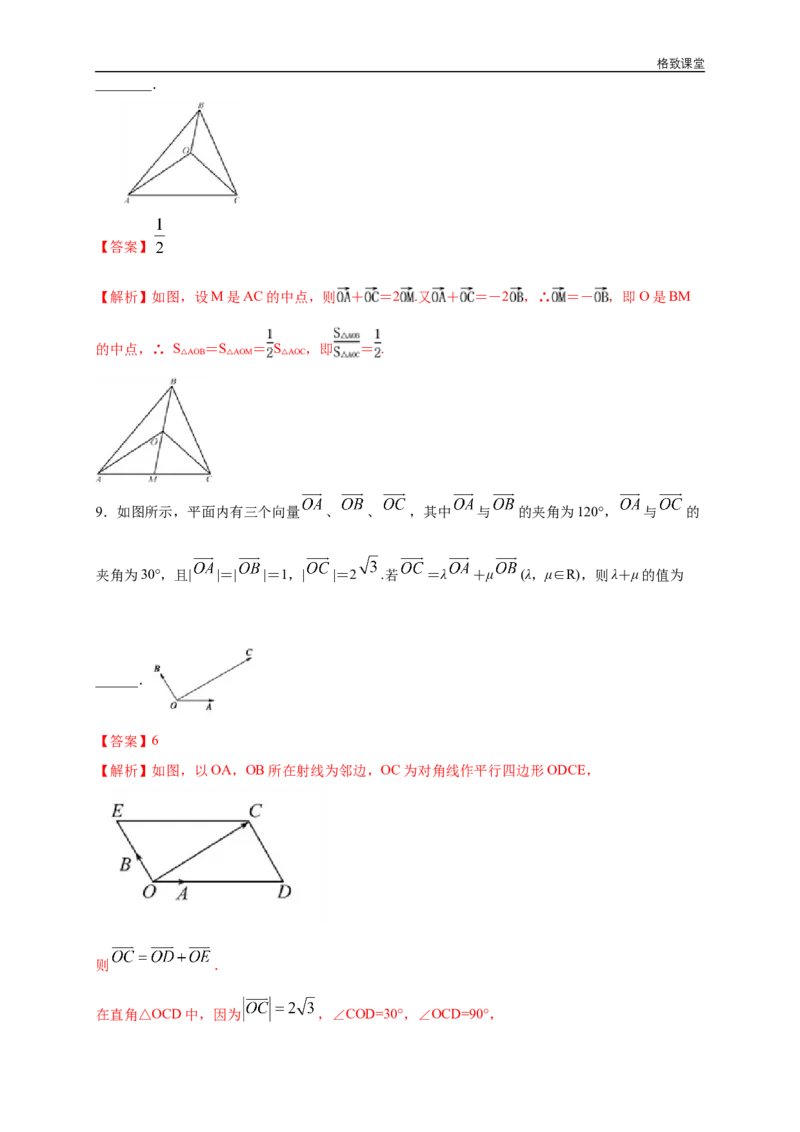
8.如图,设O是△ABC内部一点,且 + =-2 ,则△AOB与△AOC的面积之比为格致课堂
________.
【答案】
【解析】如图,设M是AC的中点,则 + =2 .又 + =-2 ,∴ =- ,即O是BM
的中点,∴ S =S = S ,即 = .
AOB AOM AOC
△ △ △
9.如图所示,平面内有三个向量 、 、 ,其中 与 的夹角为120°, 与 的
夹角为30°,且| |=| |=1,| |=2 .若 =λ +μ (λ,μ∈R),则λ+μ的值为
______.
【答案】6
【解析】如图,以OA,OB所在射线为邻边,OC为对角线作平行四边形ODCE,
则 .
在直角△OCD中,因为 ,∠COD=30°,∠OCD=90°,格致课堂
所以 , ,
故 , ,
即 ,
所以 .
10.如图所示, ,点 在由射线 、线段 及 的延长线围成的阴影区域内(不
含边界)运动,且 ,则 的取值范围是______;当 时, 的取值范围是
______.
【答案】 ;
【解析】由题意得:
设
= .
由 得
因为 ,所以 当 时,有 ,
解得
三、解答题格致课堂
11.(2019·全国高一课时练习)已知 为两个不共线的向量,若四边形 满足
,
(1)将 用 表示;
(2)证明四边形 为梯形.
【答案】(1) (2)详见解析
【解析】(1)
(2)因为 ,即 ,
所以 与 同方向,且 的长度为 的长度的2倍,
所以在四边形 中, ,且 ,
所以四边形 是梯形.
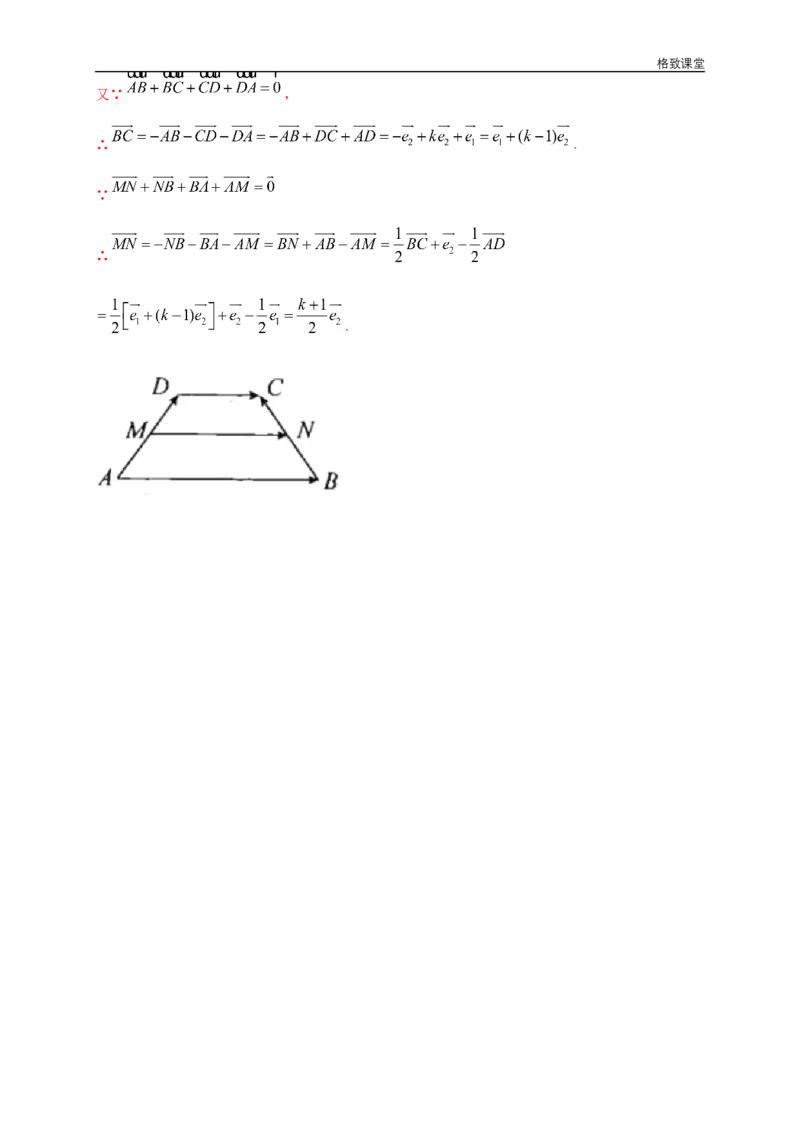
12.(2019·全国高一课时练习)在梯形ABCD中, , 分别是 的中点,
且 .设 ,选择基底 ,试写出下列向量在此基底下的分解
式: .
【答案】 , ,
【解析】如图,∵ ,且 ,
∴ .格致课堂
又∵ ,
∴ .
∵
∴
.