文档内容
2024~2025 学年度第一学期高一期中考试
数学试题
考生注意:
1.满分150分,考试时间120分钟.
2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答
题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
3.本卷命题范围:人教A版必修第一册第一章~第三章.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 设全集 , , ,则 ( )
A. B. C. D.
2. 是有理数集, 是实数集,命题 , ,则( )
A. 是真命题, ,
B. 是真命题, ,
C. 是假命题, ,
D. 是假命题, ,
3. 函数 ,则 ( )
A. B. C. D. 8
4. “ ”是“方程 有实根”的( )
.
A 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件5. 下列各组函数中不是同一函数的是( )
A. 与
B. 与
C. 与
.
D 与
6. 设 , , ,则( )
A. B.
C. D.
7. 若 在 上是减函数,则( )
A. B.
C. D.
8. 设 ,函数 表示不超过 的最大整数,例如 , .若函数
,则函数 的值域是( )
A. B.
C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列“若 ,则 ”形式的命题中,p是q的必要不充分条件的是( )
A. 若 ,则B. 若 ,则
C. 若 ,则
D. 若 ,则
10. 下列与函数有关的命题中,正确的是( )
A. 若 ,则
B. 若幂函数 的图象经过点 ,则
C. 若奇函数 在 上有最小值4,则 在 上有最大值-4
D. 若偶函数 在 是减函数,则 在 是增函数
11. (多选)设a>0,b>0,则下列不等式中一定成立的是( )
A. a+b+ ≥2 B. ≥ C. ≥a+b D. (a+b) ≥4
三、填空题:本大题共3小题,每小题5分,共15分.
12. 函数 的定义域是_________.
13. 不等式 的解集是 ,则 的解集为_________.
14. 表示 与 中的较大者,设 ,则函数
的最小值是______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知全集 ,集合 , .
(1)当 时,求 , ;(2)若 ,求a的取值范围.
16. 已知函数 .
(1)当 时,判断函数 的单调性并证明;
(2)若不等式 成立,求实数x的取值范围.
17. 幂函数 的定义域是全体实数
(1)求 的解析式;
(2)若不等式 的解集为 ,求实数 的取值范围.
18. 新时代党的治疆方略:依法治疆、团结稳疆、文化润疆、富民兴疆、长期建疆.为提升人民生活质量,
克州某乡镇全力打造“生态特色小镇”,调研发现:某种农作物的单株产量t(单位:kg)与化肥费用x(单
位:元)满足如下关系: ,其它总成本为 (单位:元),已知这种农作
物的市场售价为每千克5元,且供不应求,记该单株农作物获得的利润为 (单位:元).
(1)求 的函数关系式;
的
(2)当投入 化肥费用为多少元时,该单株农作物获得的利润最大?最大利润是多少元?
19. 已知函数 是 上的奇函数,
(1)求实数 的值;
(2)求函数 的值域.2024~2025 学年度第一学期高一期中考试
数学试题
考生注意:
1.满分150分,考试时间120分钟.
2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答
题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
3.本卷命题范围:人教A版必修第一册第一章~第三章.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 设全集 , , ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】求出全集 ,利用补集和交集的定义可求得集合 .
【详解】因为全集 , , ,
则 , ,所以, .
故选:B.
2. 是有理数集, 是实数集,命题 , ,则( )
A. 是真命题, ,
B. 是真命题, ,
C. 是假命题, ,
D. 是假命题, ,【答案】C
【解析】
【分析】根据特值可判断命题 的真假,再结合命题的否定的概念可得 .
【详解】命题 , ,
由 , ,则命题 为假命题,
且命题 的否定为 , ,
故选:C.
3. 函数 ,则 ( )
A. B. C. D. 8
【答案】B
【解析】
【分析】根据分段函数的解析式,由内到外依次求函数值即得.
【详解】因 ,则 .
故选:B.
4. “ ”是“方程 有实根”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】由 得到 有实数根满足的条件,根据真包含关系得到答案.
【详解】若方程 有实根,则 ,即 或 .
由于 是 的真子集,
故“ ”是“ 或 ”的充分不必要条件.
故选:A5. 下列各组函数中不是同一函数的是( )
A. 与
B. 与
C. 与
D. 与
【答案】D
【解析】
【分析】判断每个选项中的两个函数的定义域和对应关系是否相同,即可选择.
【详解】对A: ,且两个函数定义域均为 ,故两个函数是同一个函数,A错
误;
对B: ,且两个函数定义域均为 ,故两函数是同一个函数,
B错误;
对C: 与 的定义域都为 ,且对应关系相同,是同一个函数,C错误;
对D: 的定义域为 ,与 的定义域 不同,故不是同一个函数,D正确.
故选:D.
6. 设 , , ,则( )
A. B.
C. D.
【答案】A
【解析】
【分析】利用函数 , 和 的单调性,结合条件,即可求解.
【详解】因为 是减函数,所以 ,
因为 在 上单调递增,又 ,所以 ,又 是增函数,所以 ,则 ,
故选:A.
7. 若 在 上是减函数,则( )
A. B.
.
C D.
【答案】D
【解析】
【分析】根据分段函数的定义及单调性列不等式组,解不等式即可.
【详解】由已知函数 在 上单调递减,
当 时, 单调递减,则 ,
当 时, 单调递减,则 ,即 ,
又结合分段函数可知 ,综上所述 .
故选:D.
8. 设 ,函数 表示不超过 的最大整数,例如 , .若函数
,则函数 的值域是( )
A. B.
C. D.
【答案】C
【解析】
【分析】求得 的值域,再根据 的定义,求 的值域.【详解】因为 ,所以 ,所以 ,
①当 时, ;
②当 时, ;
③当 时, ;
④当 时, ,
所以函数 的值域为 .
故选:C.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列“若 ,则 ”形式的命题中,p是q的必要不充分条件的是( )
A. 若 ,则
B. 若 ,则
C. 若 ,则
D. 若 ,则
【答案】AD
【解析】
【分析】利用充分条件和必要条件的定义以及不等式的性质,对各个选项逐一分析判断,即可求解.
【详解】对于A,B,命题“若 ,则 ”,当 时是假命题,而命题“若 ,则
”是真命题,
所以 ,而 不能推出 ,故 是 的必要不充分条件,故A正
确,B错误;对于C,D,由 ,则 ,所以 ,即 ,
所以命题“若 ,则 ”是真命题,
而若 ,如 , , ,则命题“若 ,则 ”是假命题,
所以 可以推出 ,但 不能推出 ,
故 是 的必要不充分条件,故C错误,D正确.
故选:AD.
10. 下列与函数有关的命题中,正确的是( )
A. 若 ,则
B. 若幂函数 的图象经过点 ,则
C. 若奇函数 在 上有最小值4,则 在 上有最大值-4
D. 若偶函数 在 是减函数,则 在 是增函数
【答案】BCD
【解析】
【分析】利用换元法和待定系数法求出函数解析式,分别计算可判断 A,B;根据奇偶函数的图象对称性
特征可判断C,D.
【详解】对于A,令 得 ,故 ,故A错误;
对于B,设幂函数 ,由 得 ,
故 ,于是 ,故B正确;
对于C,因奇函数的图象关于原点对称,故C正确;对于D,因偶函数在对称区间上的单调性相反,故D正确.
故选:BCD.
11. (多选)设a>0,b>0,则下列不等式中一定成立的是( )
A. a+b+ ≥2 B. ≥ C. ≥a+b D. (a+b) ≥4
【答案】ACD
【解析】
【分析】利用基本不等式逐个分析判断即可
【详解】解:因为a>0,b>0,所以a+b+ ≥2 + ≥2 ,当且仅当a=b且2 =
即a=b= 时取等号,故A一定成立.
因为a+b≥2 >0,所以 ≤ = ,当且仅当a=b时取等号,所以 ≥ 不一定成立,
故B不成立.
因为 ≤ = ,当且仅当a=b时取等号,
所以 = =a+b- ≥2 - ,当且仅当a=b时取等号,
所以 ≥ ,所以 ≥a+b,故C一定成立.
因为(a+b) =2+ + ≥4,当且仅当a=b时取等号,故D一定成立,
故选:ACD.
三、填空题:本大题共3小题,每小题5分,共15分.
12. 函数 的定义域是_________.【答案】
【解析】
【分析】根据函数解析式有意义可得出关于实数 的不等式组,由此可得出原函数的定义域.
【详解】对于函数 ,有 ,解得 且 且 .
因此,函数 的定义域为 .
故答案为: .
13. 不等式 的解集是 ,则 的解集为_________.
【答案】
【解析】
【分析】分析可知, ,且关于 的方程 的两根分别为 、 ,利用韦达定理可得出
、 与 的等量关系,然后利用二次不等式的解法可得出不等式 的解集.
【详解】因为不等式 的解集是 ,则 ,
且关于 的方程 的两根分别为 、 ,
由韦达定理可得 ,可得 ,
所以,不等式 即为 ,
即 ,解得 ,
故不等式 的解集为 .
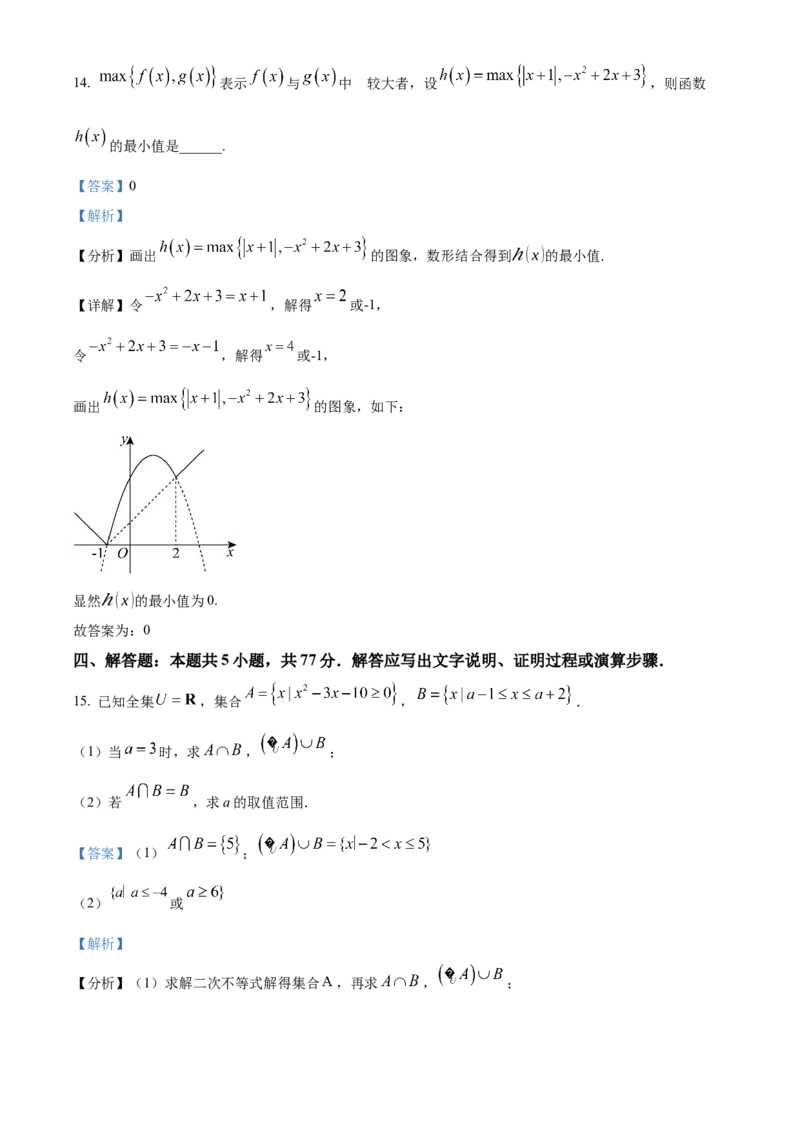
故答案为: .14. 表示 与 中 的较大者,设 ,则函数
的最小值是______.
【答案】0
【解析】
【分析】画出 的图象,数形结合得到ℎ(x)的最小值.
【详解】令 ,解得 或-1,
令 ,解得 或-1,
画出 的图象,如下:
显然ℎ(x)的最小值为0.
故答案为:0
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知全集 ,集合 , .
(1)当 时,求 , ;
(2)若 ,求a的取值范围.
【答案】(1) ;
(2) 或
【解析】
【分析】(1)求解二次不等式解得集合 ,再求 , ;(2)由题可得 ,根据集合的包含关系,列出关于 的不等式,求解即可.
【小问1详解】
由题意可得 或 ,当 时, ,
故 ; ,故 .
【小问2详解】
因为 ,所以 ,
又 ,则 或 ,解得 或 ,
即 的取值范围为 或 .
16. 已知函数 .
(1)当 时,判断函数 的单调性并证明;
(2)若不等式 成立,求实数x的取值范围.
【答案】(1) 在 上单调递增,证明见解析
(2)
【解析】
【分析】(1)根据函数单调性的定义判断并证明即可;
(2)结合函数单调性将不等式转化即可得解集.
【小问1详解】
在 上单调递增,理由如下:
任取 , ,且 ,.
因为 ,所以 , , ,
所以 ,即 ,可得 ,
所以 在 上单调递增.
【小问2详解】
因为 , ,
由(1)得 在 上单调递增,
因为 ,所以 ,
即 ,解得: 或 ,
所以实数x的取值范围是 .
17. 幂函数 的定义域是全体实数
(1)求 的解析式;
(2)若不等式 的解集为 ,求实数 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据幂函数 定的义可得出关于实数 的等式,解出 的值,再由函数 的定义域为R进
行检验,即可得解;
(2)分析可知,不等式 对任意的实数 恒成立,分 、 两种情况讨论,在 时,直接检验即可;在 时,利用二次不等式恒成立,可得出关于实数 的不等式组,
综合可得出实数 的取值范围.
【小问1详解】
因为 是幂函数,所以 ,
化简得 ,解得 或 ,
当 时, ,该函数 的定义域为R,满足题意;
当 时, 的定义域为 ,不满足题意,
所以 的解析式为 .
【小问2详解】
不等式 即 ,其解集为 ,
则 对任意的实数 恒成立,
当 时, ,得 ,不合题意;
当 时,则有 ,解得 .
因此,实数 的取值范围是 .
18. 新时代党的治疆方略:依法治疆、团结稳疆、文化润疆、富民兴疆、长期建疆.为提升人民生活质量,
克州某乡镇全力打造“生态特色小镇”,调研发现:某种农作物的单株产量t(单位:kg)与化肥费用x(单
位:元)满足如下关系: ,其它总成本为 (单位:元),已知这种农作
物的市场售价为每千克5元,且供不应求,记该单株农作物获得的利润为 (单位:元).(1)求 的函数关系式;
(2)当投入的化肥费用为多少元时,该单株农作物获得的利润最大?最大利润是多少元?
【答案】(1) ,
(2)当投入的化肥费用为 元时,该单株农作物获得的利润最大为
【解析】
【分析】(1)考虑 和 ,计算利润得到解析式;
(2)根据函数单调性和均值不等式分别计算分段函数最值,比较得到答案.
【小问1详解】
当 时, ;
当 时, ;
综上所述: ;
【小问2详解】
当 时, ,
所以 在 上单调递减,在 上单调递增,又 , ,
所以 ;
当 时, ,
当且仅当 ,即 时等号成立,
综上所述:当投入的化肥费用为 元时,该单株农作物获得的利润最大为 .
19. 已知函数 是 上的奇函数,
(1)求实数 的值;
(2)求函数 的值域.
【答案】(1)
(2)答案见解析
【解析】
【分析】(1)根据奇函数的性质,可得 ,再利用条件 ,可求得 ,即可求解;
(2)利用函数单调性的定义得到 在区间 上单调递减,从而得到 ,令
,将问题转化成求 的值域,再利用二次函数的性质,即可求
解.
【小问1详解】
因为函数 是 上的奇函数,则 ,
又 , ,得到 ,所以 ,
此时有 ,所以 , ,满足题意,故实数 , .
【小问2详解】
由(1)知 ,任取 ,则 ,
因为 ,则 ,得到 ,
所以 ,即 ,所以 在区间 上单调递减,
所以 时, ,
令 ,由 ,
得到 ,对称轴为 ,
当 时, 在区间 上单调递增,此时, ,
当 时, 在区间 上单调递减,此时, ,
当 时, ,
① 时, ,
② 是, ,
综上,当 时,函数 的值域为 ,
当 时,函数 的值域为 ,
当 时,函数 的值域为 ,当 时,函数 的值域为 .