文档内容
2024-2025 学年安徽省皖南八校高一下学期 4 月期中考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数 ,则 的共轭复数在复平面内对应的点位于( )
A.第一象限 =(1−2 )(3B−.第2 二) 象限 C.第三象限 D.第四象限
2.在三棱台 ′ ′′中,截去三棱锥 ′ ′′,则剩余部分是( )
A.三棱锥 − B .三棱台 C.−四 棱锥 D.三棱柱
3. , 是平面内不共线的两向量,已知 , , ,若 , , 三点
共线 ��1�, �则�2� 的值为( ) ��� ��= ��1�− ��2� ��� ��=3 ��1�+4 ��2� ��� ��=4 ��1�+ ��2�
A. B. C. D.
7 7
−2 2 −3 3
4.已知 的内角 , , 所对的边分别为 , , , , ,若满足条件的 有两个,则
的值可能 △ 为 ( ) = 4 =10 △
A. B. C. D.
5.已7知 , 是两个单位向量,5 且2向量 在向量9 上的投影向量为 10,则向量 , 的夹角 ( )
� � � � � �+4� � � � 3� � � � � � =
A. B. C. D.
6.如3 图,一块三角形铁皮,其4一角已破裂,小明为6了了解原铁皮的规格 − ,3现测得如下数据: ,
, , ,则破裂的断点 , 两点间距离为( ) =20 3
=10 =14 = = 6
A. B. C. D.
7.如10图,3 有 两个相同的直三棱15柱 ,高为 ,底面三1角0 形2的 三边长分别为14 , , ,用这两个三棱柱拼成一个
三棱柱,在所有可能组成的三棱柱中,表1 面积不可能为( ) 3 4 5
A. B. C. D.
36 38 40 42
第 页,共 页
1 88.已知 中, , , 是 外接圆的圆心,则 的最大值为( )
△ = 3 ∠ = 3 △ ��� ��⋅ ��� ��− ��� ��⋅ ��� ��
A. B. C. D.
二、1多选题:本题共3小题,共3 18分。在每小题2给出的选项中,有多2项符3合题目要求。
9.已知向量 , ,则下列选项正确的是( )
A. , 能作� �为=平(1面,3内) 所� �有=向(2量,−的4一)组基底
B.� � � �
C.(� �+� �)⊥� �
D.
|� �,+2的 � � 夹|=角1为0
3
10.� �已知 � � , 为复4 数,则下列说法正确的是( )
A.若 1 2 ,则 B.若 ,则
2 2
C.若| 1|=| 2| ,则 1 = 2 D. | 1− 2|=0 1 = 2
11.如 图1+, 一2 >圆0锥的侧 面2 >展−开 1图中, ,弧 | 长1 为2|= | 1||, 2则| 下列说法正确的是( )
=3 2 3
A.该圆锥的侧面积为
B.该圆锥的体积为 3 3
C.该圆锥可以整体放6入 半径为 的球内
7
D.该圆锥可以整体放入边长为4 的正方体中
三、填空题:本题共3小题,每2小2题5分,共15分。
12.在复平面内,向量 对应的复数 , 绕点 逆时针旋转 后对应的复数为 ,则
∘
. ��� �� 1 =1+2 ��� �� 90 2
| 1− 2|=
第 页,共 页
2 813.如图, ′ ′ ′为水平放置的 的直观图,其中 ′ ′ ,′ ′ ′′ ,则
的面积为△ . △ =2 = = 5 △
14.有长度分别为 , , , 的线段各 条,首尾依次相连地放在桌面上,可组成周长为 的四边形,
如图, , 1 2 ,3 4 , 1 ,则组成的四边形 面积的最大值为 .10
=1 =3 =2 =4
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15. 本小题 分
已知(复数 和1它3的共) 轭复数 满足 .
求 3 + =4+4
(1)若 ;是关于 的方程 的一个根,求复数 的模长.
2
(126). 本 小题 分 + + =0( , ∈ ) +
( 15 )
记 的内角 , , 的对边长分别为 , , ,已知 .
cos + cos
△求 2 = cos
(1) ;
若 , ,求 的面积.
6
( 1 2 7 ). 本 小=题1 sin分 +sin = 2 △
如图(,已知圆15台的)轴截面为梯形 , , ,梯形 的面积为 .
=4 =2 6 2
求圆台的体积
(1)在圆台的侧面上; ,从点 到点 的最短路径长度是多少
(2) ?
第 页,共 页
3 818. 本小题 分
( 17 )
在平行四边形 中, , , , 是线段 的中点,点 在直线 上,且
. =4 =6 ∠ = 3 ��� ��= ��� ��(−
1≤ ≤ 1)
当 时,求 的值
1
(1) =3 ��� ��⋅ ��� �� ;
当 时, 与 交于点 , ,求 的值
1
(2)
求
=2
的最
小值
.
��� ��= ��� ��+ ��� �� − ;
(139). 本 ��小� �⋅题 ��� �� 分
在平(面直角坐17标系) 中,对于非零向量 , ,满足 ,则称
| 1 2− 2 1|
� �=( 1, 1) � �=( 2, 2) (� �,� �)= 2 2 2 2 (� �,� �)
为这两个向量的“协方差”. 1+ 1⋅ 2+ 2
若 ,证明: .
(1)已知 (向� �,� 量�)=,0 的夹角为� �//,� �向量 , 的夹角为 ,且 证明: .
(2)在 �中 � ,� �线段 , 1 为 � � 的� � 两条内角 平2 分线 ,(� 点�,� �),= 分(� �别,� �在). , sin边 上1 =,sin 2 ,且
∘
(3) △ ,求 △ =60 3 ��� ��⋅
��� ��=2 ��� ��⋅ ��� �� ( ��� �, ��� ��).
第 页,共 页
4 8参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10 .
11.
12.
13. 10
14.4 2
15.2解:6 设 ,
则 (1) , = + ( , ∈ )
则 = − ,
3 + =3( + )+( − )=4 +2 =4+4
所以 ,解得 , ,
4 =4
=1 =2
故 ;
2 =4
=1是+关2于 的方程 的一个根,
2
(2)是∵关 于 的方 程 + + =0( , ∈的 另) 一个根,
2
∴ + + =0( , ∈ )
,解得 , ,
1+2 +1−2 =−
∴ =−2 =5
(1+2 )(1−2 )= .
∴16|. 解+: |=|5−2 | = 29 ,
(1) ∵ 2 cos = cos + cos ,
∴ 2sin cos, =sin cos +sin cos = sin ( + )= sin
∵ ≠0
得 ,
1
又cos =2,
∈(0, )
第 页,共 页
5 8则 .
= 3
, ,
(2 由 ) 正 ∵ 弦 = 定3理得 =1 ,
1 2
∴ sin =sin =sin = 3 = 3
2
则 , ,
2 2
sin = 3 sin = 3
,
6
∵ sin +sin = 2
,
2 2 6
∴得 3 + 3 =,2
由余 +弦 定=理得2 ,
2 2
1= + −2 cos 3
得 ,
1
=3
则 的面积 .
1 3
17 △ .解 : 由 =2, sin =,1得2圆台的下底面的半径为 ,上底面的半径为 ,
(1) =4 =2 =2 =1
设圆台的高为 ,则 ,所以 ,
1
ℎ 2×(2+4)⋅ℎ =6 2 ℎ=2 2
所以圆台的体积为 .
1 2 2 1 2 2 14 2
=3( + + ) ℎ=3(1 +2 +1×2) ⋅2 2= 3
在梯形 中, ,即母线长为 .
2 2
(如2)图,由圆 台 性 质, 延 长= ,(2−,1) +(交2于2点) =,3 3
1
由 与 相似,得 ,即 ,解得 .
1
△ △ + = +3=2 =3
设该圆台的侧面展开图的圆心角为 ,则 ,所以 ,
2
在侧面展开图中,连接 , ,则 从点 3 到 = 的 2 最 短 = 路 2 径 为线段 =,3
又在 中, , , ,
1 2
△ =3 =6 ∠ =2× 3 =3
由余弦定理得 ,所以 .
2 2 2 2 2 1
验证知,由 = , + , −2 ⋅ , c 得 os3 = 6,此+3时−2×6×,3恰×与2扇=形3弧3 所在圆相切
2 2 2
=3 =6 =3 3 = + ⊥
第 页,共 页
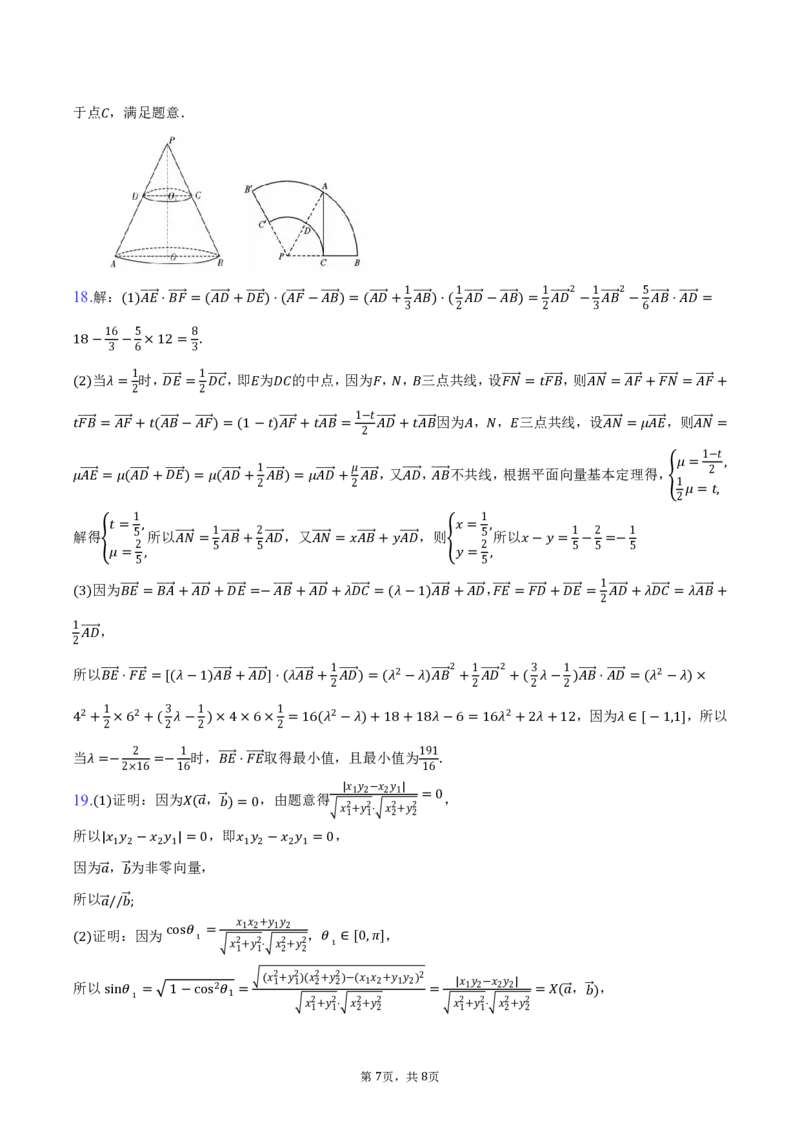
6 8于点 ,满足题意.
18.解:
2 2
1 1 1 1 5
(1) ��� ��⋅ ��� ��=( ��� ��+ ��� ��)⋅( ��� ��− ��� ��)=( ��� ��+3 ��� ��)⋅(2 ��� ��− ��� ��)= 2 ��� �� −3 ��� �� −6 ��� ��⋅ ��� ��=
.
16 5 8
18− 3 −6×12= 3
当 时, ,即 为 的中点,因为 , , 三点共线,设 ,则
1 1
(2) =2 ��� ��=2 ��� �� ��� ��= ��� �� ��� ��= ��� ��+ ��� ��= ��� ��+
因为 , , 三点共线,设 ,则
1−
��� ��= ��� ��+ ( ��� ��− ��� ��)=(1− ) ��� ��+ ��� ��= 2 ��� ��+ ��� �� ��� ��= ��� �� ��� ��=
,又 , 不共线,根据平面向量基本定理得,
1−
1 = 2 ,
��� ��= ( ��� ��+ ��� ��)= ( ��� ��+2 ��� ��)= ��� ��+2 ��� �� ��� �� ��� �� 1
2 = ,
解得 所以 ,又 ,则 所以
1 1
=5, 1 2 =5, 1 2 1
2 ��� ��=5 ��� ��+5 ��� �� ��� ��= ��� ��+ ��� �� 2 − =5−5=−5
因为
=5, =5, ,
1
(3) ��� ��= ��� ��+ ��� ��+ ��� ��=− ��� ��+ ��� ��+ ��� ��=( −1) ��� ��+ ��� �� ��� �= ��� ��+ ��� ��=2 ��� ��+ ��� ��= ��� ��+
,
1
2 ��� ��
所以
2 2
1 2 1 3 1 2
��� ��⋅ ��� �=[( −1) ��� ��+ ��� ��]⋅( ��� ��+2 ��� ��)=( − ) ��� �� +2 ��� �� +(2 −2) ��� ��⋅ ��� ��=( − )×
,因为 ,所以
2 1 2 3 1 1 2 2
4 +2×6 +(2 −2)×4×6×2=16( − )+18+18 −6=16 +2 +12 ∈ [−1,1]
当 时, 取得最小值,且最小值为 .
2 1 191
=−2×16=−16 ��� ��⋅ ��� � 16
19. 证明:因为 , ,由题意得 ,
| 1 2− 2 1|
所以(1) (� �, � 即 �)=0 , 1 2 + 1 2 ⋅ 2 2 + 2 2 =0
因为| ,1 2为−非 2零 1向|=量0, 1 2− 2 1 =0
所以� � � �
证� �明//: � �;因为 , ,
1 2+ 1 2
(2) cos 1 = 1 2 + 1 2 ⋅ 2 2 + 2 2 1 ∈[0, ]
所以 , ,
2 2 2 2 2
2 ( 1+ 1)( 2+ 2)−( 1 2+ 1 2) | 1 2− 2 2|
sin 1 = 1−cos 1 = 2 2 2 2 = 2 2 2 2 = (� � � �)
1+ 1⋅ 2+ 2 1+ 1⋅ 2+ 2
第 页,共 页
7 8同理 , ,
因为sin ,2 = (� � �, �) ,所以 .
因 为(� � � �)= (� � � �) ,sin 1 =sin 2
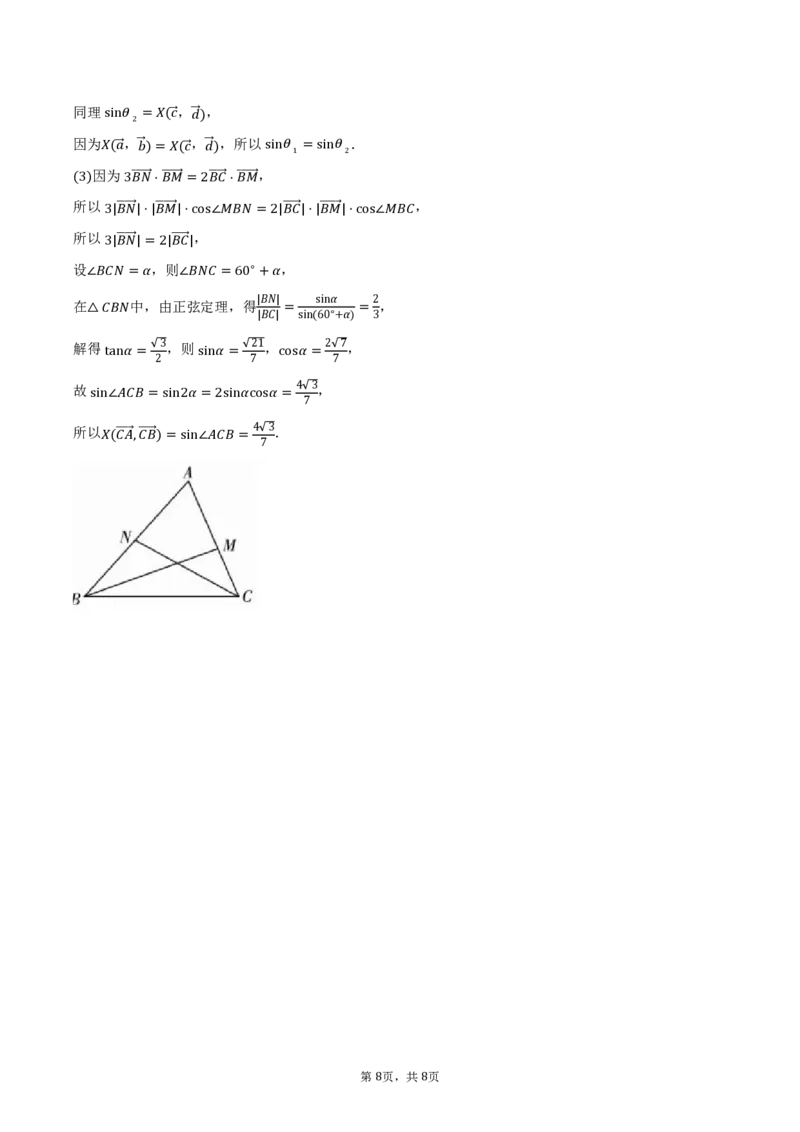
(所3)以 3 ��� ��⋅ ��� ��=2 ��� ��⋅ ��� �� ,
所以3| ��� ��|⋅| ��� ��|⋅c,os∠ =2| ��� ��|⋅| ��� ��|⋅cos∠
设 3| ��� ��|=,2则| ��� ��| ,
∘
∠ = ∠ =60 +
在 中,由正弦定理,得 ,
| | sin 2
△ | | =sin(60 ∘ + )=3
解得 ,则 , ,
3 21 2 7
tan = 2 sin = 7 cos = 7
故 ,
4 3
sin∠ =sin2 =2sin cos = 7
所以 .
4 3
( ��� �, ��� ��)= sin∠ = 7
第 页,共 页
8 8