文档内容
格致课堂
8.1 基本几何图形
第 1 课时 棱柱、棱锥、棱台
一、选择题
1.下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后的图形是( )
A. B. C. D.
【答案】B
【解析】
将其折叠起来,变成正方体后的图形中,相邻的平面中三条线段是平行线,排除A,C;相邻平面只有两
个是空白面,排除D;
故选B
2.一个棱锥的各条棱都相等,那么这个棱锥必不是( )
A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥
【答案】D
【解析】正六棱锥的底面是个正六边形,正六边形共由6个等边三角形构成,设每个等边三角形的边长为
,正六棱锥的高为 ,正六棱锥的侧棱长为 ,由正六棱锥的高 、底面的半径 、侧棱长 构成直角
三角形得, ,故侧棱长 和底面正六边形的边长 不可能相等.
故选D.格致课堂
3.下列几何体中棱柱有( )
A.5个 B.4个 C.3个 D.2个
【答案】D
【解析】
由棱柱的定义及几何特征,①③为棱柱.故选D.
4.用一个平面去截一个四棱锥,截面形状不可能的是 ( )
A.四边形 B.三角形 C.五边形 D.六边形
【答案】D
【解析】根据一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,而四棱锥最多只有5
个面,则截面形状不可能的是六边形,故选D.
5.(多选题)给出下列命题,其中假命题是( )
A.棱柱的侧棱都相等,侧面都是全等的平行四边形;
B.用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台;
C.若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;
D.棱台的侧棱延长后交于一点,侧面是等腰梯形.
【答案】ABD
【解析】对于A,棱柱的侧面不一定全等,故错误;
对于B,由棱台的定义可知只有当平面与底面平行时,所截部分才是棱台,故错误;
对于C,若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直,
比如正方体中共点的三个相邻平面,故正确;
对于D,棱台的侧面不一定是等腰三角形,故错误;
故选ABD .
6.(多选题)正方体的截面可能是( )
A.钝角三角形 B.直角三角形 C.菱形 D.正六边形
【答案】CD格致课堂
【解析】
如图所示截面为三角形ABC,OA=a,OB=b,OC=c,
∴ ,
∴
∴∠CAB为锐角,同理∠ACB与∠ABC也为锐角,即△ABC为锐角三角形,
∴正方体的截面若是三角形,则一定是锐角三角形,
不可能是钝角三角形和直角三角形,A、B错误;
若是四边形,则可以是梯形(等腰梯形)、平行四边形、菱形、矩形、正方形,
但不可能是直角梯形,C正确;
正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,
如图为正六边形,故若是六边形,则可以是正六边形,D正确.
故选:CD.
二、填空题
7.一棱柱有10个顶点,其所有的侧棱长的和为60 cm,则每条侧棱长为________cm.
【答案】12
【解析】该棱柱为五棱柱,共有5条侧棱,每条侧棱长都相等,∴每条侧棱长为12 cm.
8.如图,M是棱长为2 cm的正方体ABCD-ABC D 的棱CC 的中点,沿正方体表面从点A到点M的最短
1 1 1 1 1
路程是________cm.
【答案】
【解析】 由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分格致课堂
别为2 cm,3 cm,故两点之间的距离是 cm.若以BB 为轴展开,则A,M两点连成的线段所在的直角三角
1
形的两直角边的长度分别为1,4,故两点之间的距离是 cm.故沿正方体表面从点A到点M的最短路程是
cm.
9.下列说法中正确的为________(填序号).
(1)棱柱的侧棱长相等,侧面都是平行四边形:(2)各侧面都是正方形的四棱柱一定是正方体;(3)
正棱锥的侧面是等边三角形;(4)有两个面互相平行,其余各面都是等腰梯形的几何体是棱台.
【答案】(1)
【解析】(1)正确,由棱柱定义可知,棱柱的侧棱相互平行且相等,所以侧面均为平行四边形;(2)不
正确,上、下底面是菱形,各侧面是全等的正方形的四棱柱不一定是正方体;(3)不正确,正棱锥的侧
面都是等腰三角形,不一定是等边三角形;(4)不正确,用反例去检验,如图,显然错误图.
故答案为:(1)
10.一个棱台至少有________个面,面数最少的棱台有________个顶点,有________条棱.
【答案】5 6 9
【解析】面数最少的棱台是三棱台,共有5个面,6个顶点,9条棱.
三、解答题
11.如图所示是一个三棱台ABC-A′B′C′,试用两个平面把这个三棱台分成三部分,使每一部分都是一个
三棱锥.
【答案】见解析
【解析】过A′,B,C三点作一个平面,再过A′,B,C′作一个平面,就把三棱台ABC-A′B′C′分成三部分,
形成的三个三棱锥分别是A′-ABC,B-A′B′C′,A′-BCC′.(答案不唯一)
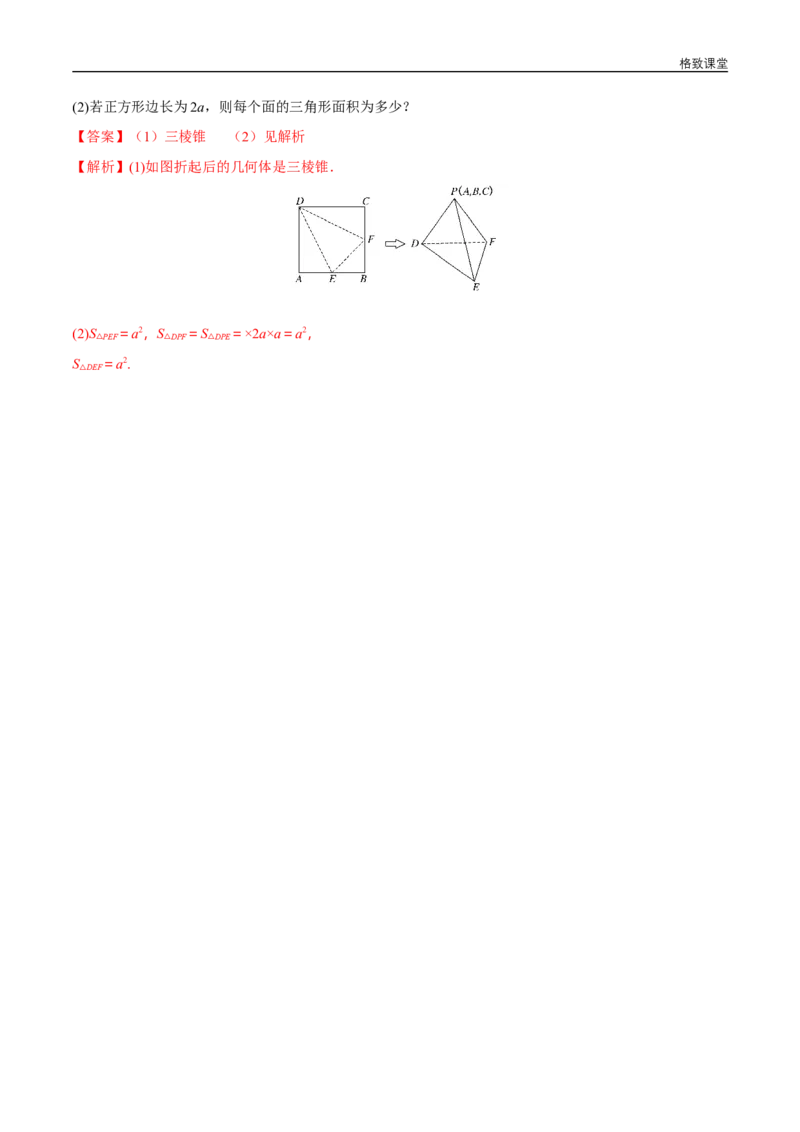
12.如图在正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C
重合,重合后记为点P.
问:(1)折起后形成的几何体是什么几何体?格致课堂
(2)若正方形边长为2a,则每个面的三角形面积为多少?
【答案】(1)三棱锥 (2)见解析
【解析】(1)如图折起后的几何体是三棱锥.
(2)S =a2,S =S =×2a×a=a2,
PEF DPF DPE
△ △ △
S =a2.
DEF
△