文档内容
期末模拟卷 2
一、单选题(本大题共8小题,共40.0分)
复数 为虚数单位 在复平面内对应的点位于
1.
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
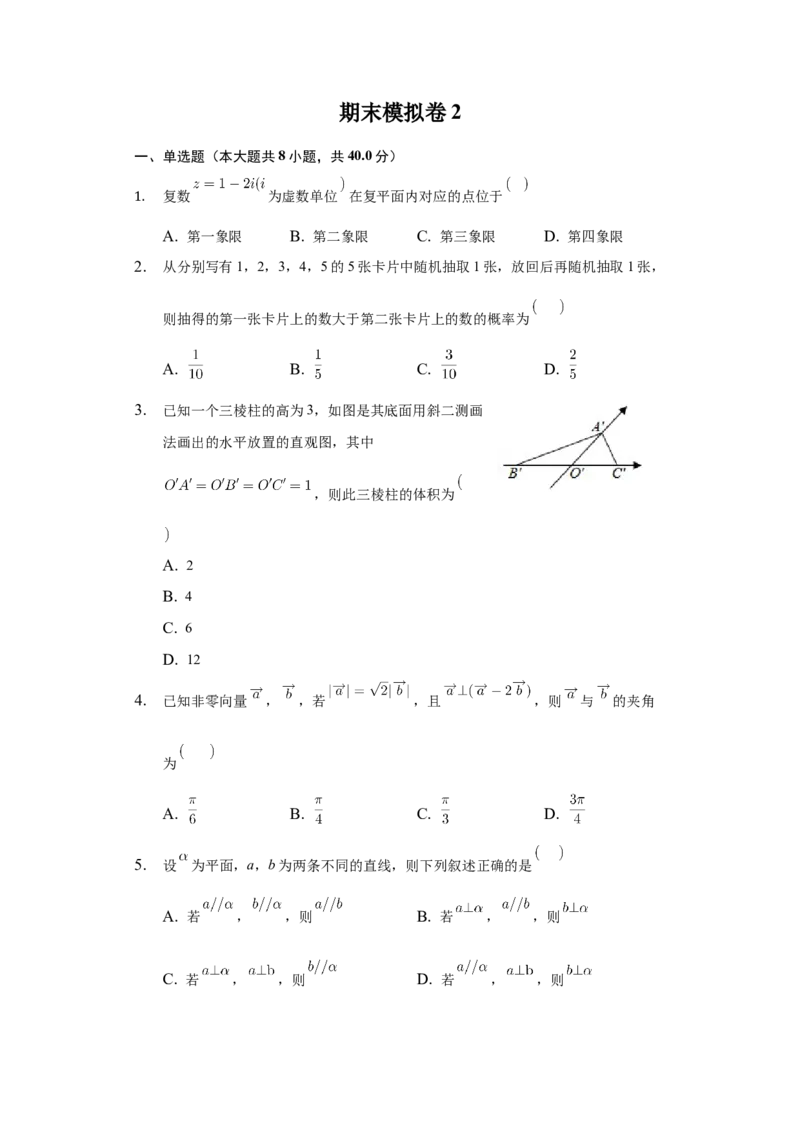
3. 已知一个三棱柱的高为3,如图是其底面用斜二测画
法画出的水平放置的直观图,其中
,则此三棱柱的体积为
A. 2
B. 4
C. 6
D. 12
4. 已知非零向量 , ,若 ,且 ,则 与 的夹角
为
A. B. C. D.
5. 设 为平面,a,b为两条不同的直线,则下列叙述正确的是
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则6. 已知圆锥的顶点为P,母线PA,PB所成角的余弦值为 ,PA与圆锥底面所成角
为 ,若 的面积为 ,则该圆锥的体积为
A. B. C. D.
7. 已知数据 的方差为4,若 ,则
新数据 的方差为
A. 16 B. 13 C. D.
8. 在 中,A,B,C所对的边分别是a,b,c,若 ,且
,则
A. 3 B. 4 C. 5 D. 6
二、多选题(本大题共4小题,共20.0分)
9. 有甲 乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订
一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I
为“一种报纸也不订” 下列命题正确的是
A. E与G是互斥事件 B. F与I是互斥事件,且是对立事件
C. F与G不是互斥事件 D. G与I是互斥事件
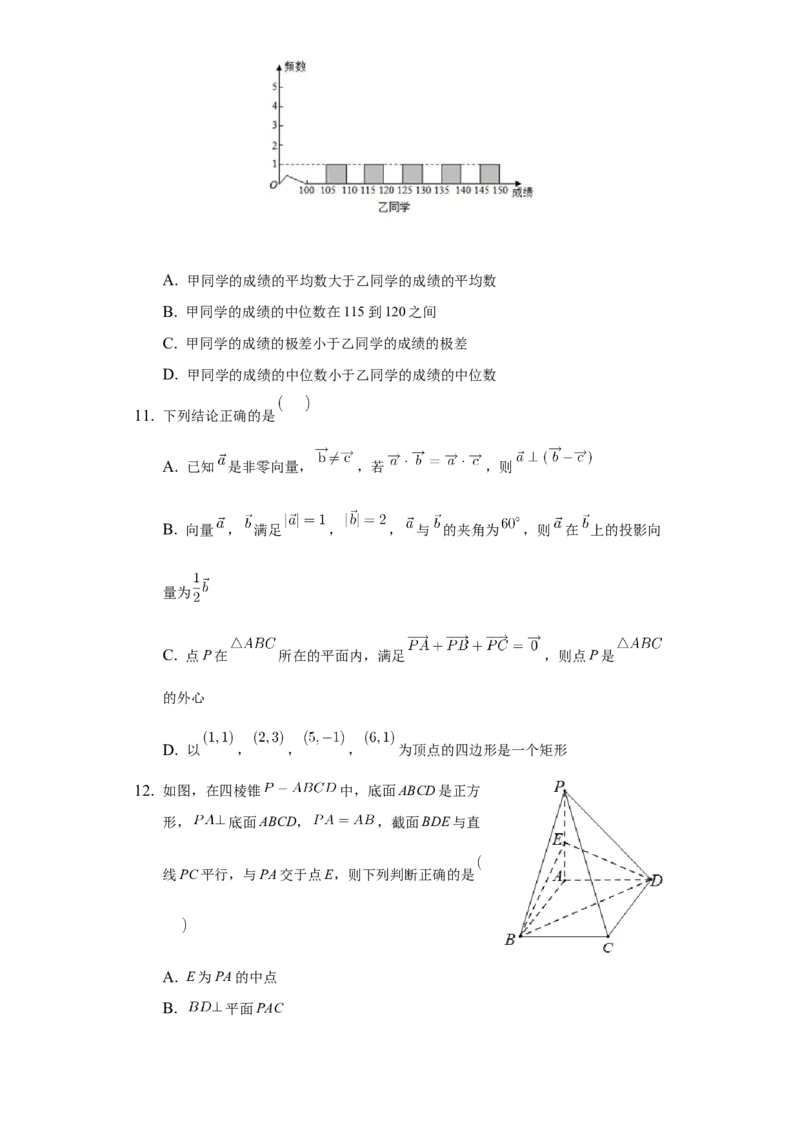
10. 下面是甲、乙两位同学高三上学期的5次联考的数学成绩,现只知其从第1次到
第5次分数所在区间段分布的条形图 从左至右依次为第1至第5次 ,则从图中
可以读出一定正确的信息是A. 甲同学的成绩的平均数大于乙同学的成绩的平均数
B. 甲同学的成绩的中位数在115到120之间
C. 甲同学的成绩的极差小于乙同学的成绩的极差
D. 甲同学的成绩的中位数小于乙同学的成绩的中位数
11. 下列结论正确的是
A. 已知 是非零向量, ,若 ,则
B. 向量 , 满足 , , 与 的夹角为 ,则 在 上的投影向
量为
C. 点P在 所在的平面内,满足 ,则点P是
的外心
D. 以 , , , 为顶点的四边形是一个矩形
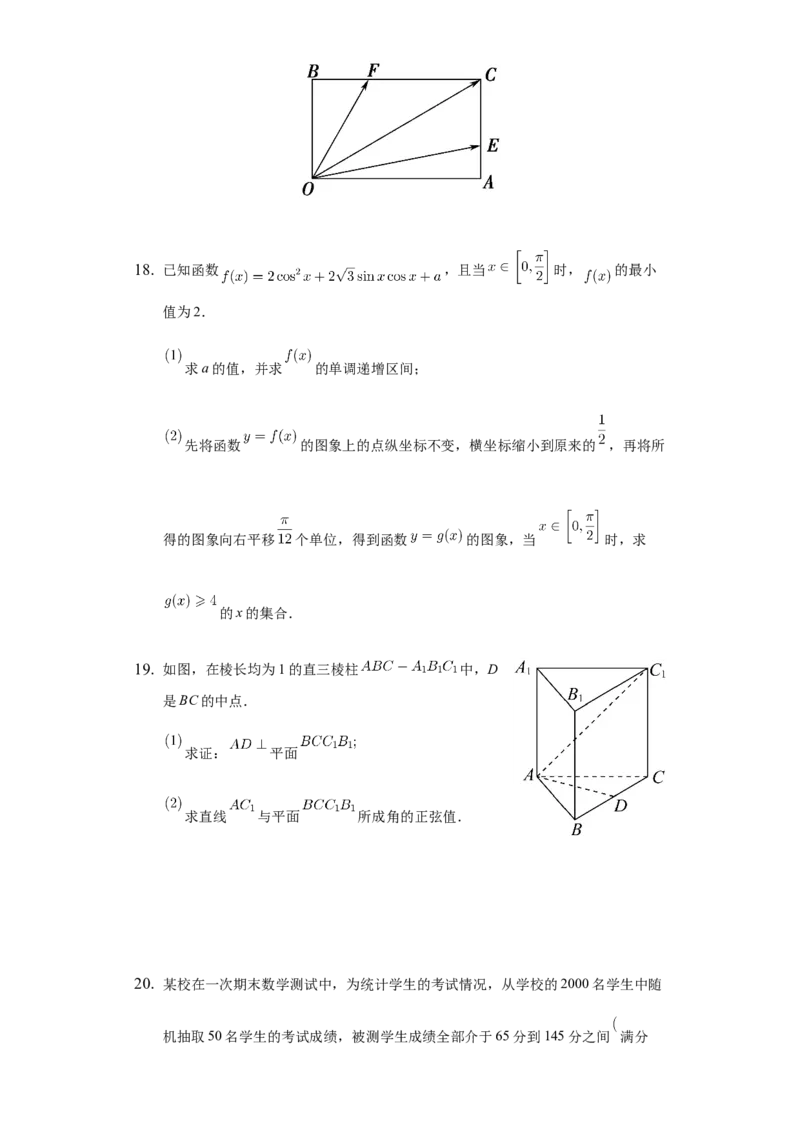
12. 如图,在四棱锥 中,底面ABCD是正方
形, 底面ABCD, ,截面BDE与直
线PC平行,与PA交于点E,则下列判断正确的是
A. E为PA的中点
B. 平面PACC. PB与CD所成的角为
D. 三棱锥 与四棱锥 的体积之比等于 .
三、填空题(本大题共4小题,共20.0分)
13. 若复数z满足方程 ,则 .
14. 如图,在平行四边形ABCD中,M,N分别为AD,AB上的点,且
,MN交于点 若 ,则 的值为 .
15. 某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出
两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是
,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一
轮的概率等于 .
16. 如图,在正方体 中,点O为线段
BD的中点,设点P在线段 上,直线OP与平面
所成的角为 ,则 的最小值 ,最大
值 .
四、解答题(本大题共6小题,共70.0分)
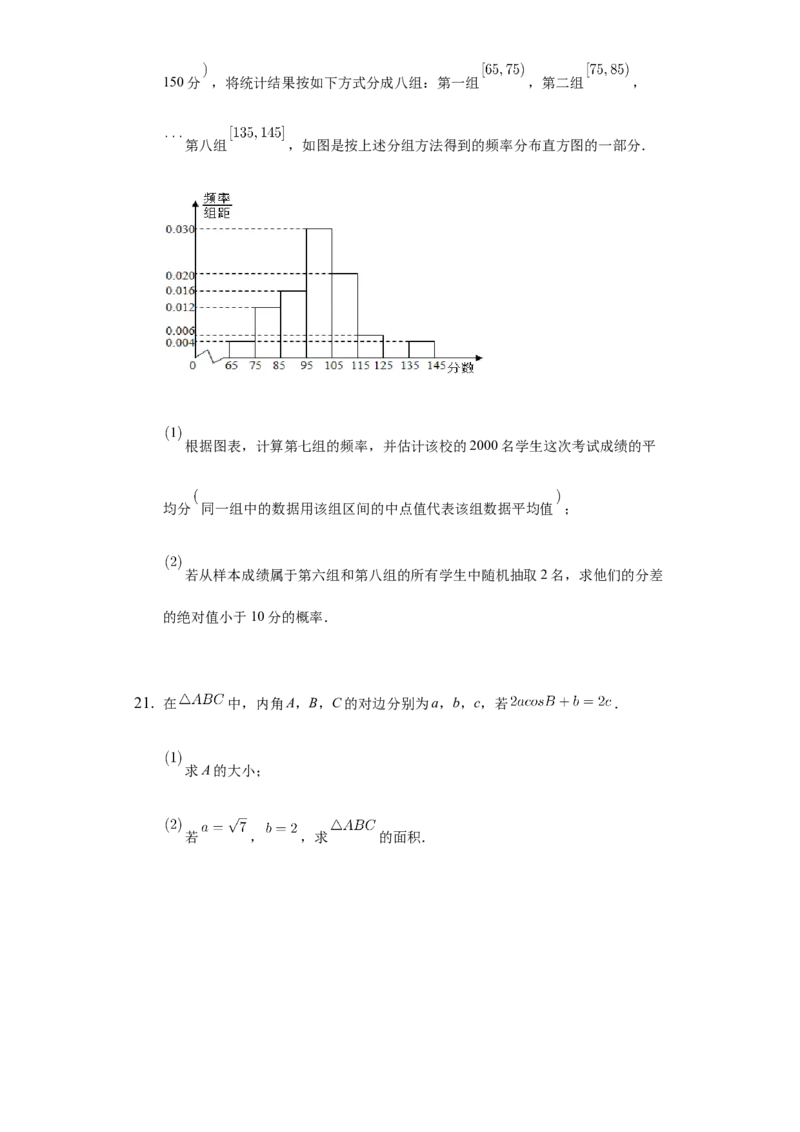
17. 如图,在矩形OACB中,E和F分别是边AC和BC上
的点,满足 , ,若 ,其中 ,
R,求 , 的值.18. 已知函数 ,且当 时, 的最小
值为2.
求a的值,并求 的单调递增区间;
先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的 ,再将所
得的图象向右平移 个单位,得到函数 的图象,当 时,求
的x的集合.
19. 如图,在棱长均为1的直三棱柱 中,D
是BC的中点.
求证: 平面
求直线 与平面 所成角的正弦值.
20. 某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随
机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间 满分150分 ,将统计结果按如下方式分成八组:第一组 ,第二组 ,
第八组 ,如图是按上述分组方法得到的频率分布直方图的一部分.
根据图表,计算第七组的频率,并估计该校的2000名学生这次考试成绩的平
均分 同一组中的数据用该组区间的中点值代表该组数据平均值 ;
若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差
的绝对值小于10分的概率.
21. 在 中,内角A,B,C的对边分别为a,b,c,若 .
求A的大小;
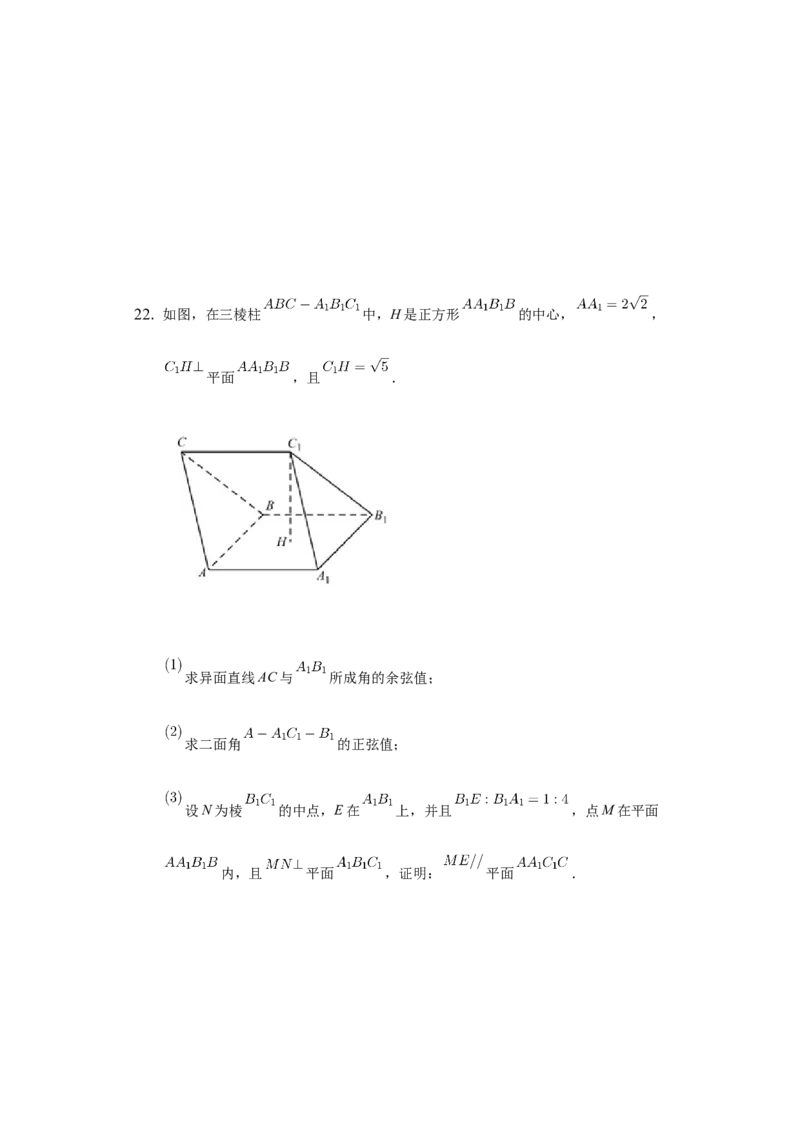
若 , ,求 的面积.22. 如图,在三棱柱 中,H是正方形 的中心, ,
平面 ,且 .
求异面直线AC与 所成角的余弦值;
求二面角 的正弦值;
设N为棱 的中点,E在 上,并且 ,点M在平面
内,且 平面 ,证明: 平面 .