文档内容
格致课堂
8.6.2 直线与平面垂直
第2课时 直线与平面垂直的性质
(用时45分钟)
【选题明细表】
知识点、方法 题号
线面垂直性质定理的应用 1,2,4,5,7,8
空间距离 3,6
综合应用 9,10,11,12
基础巩固
1.已知直线 平面 ,直线 ,则( )
A. B.
C. 异面 D. 相交而不垂直
【答案】A
【解析】根据线面垂直的定义,若直线与平面垂直,则直线垂直与该平面内的任意一条直线,因此 ,
故选A
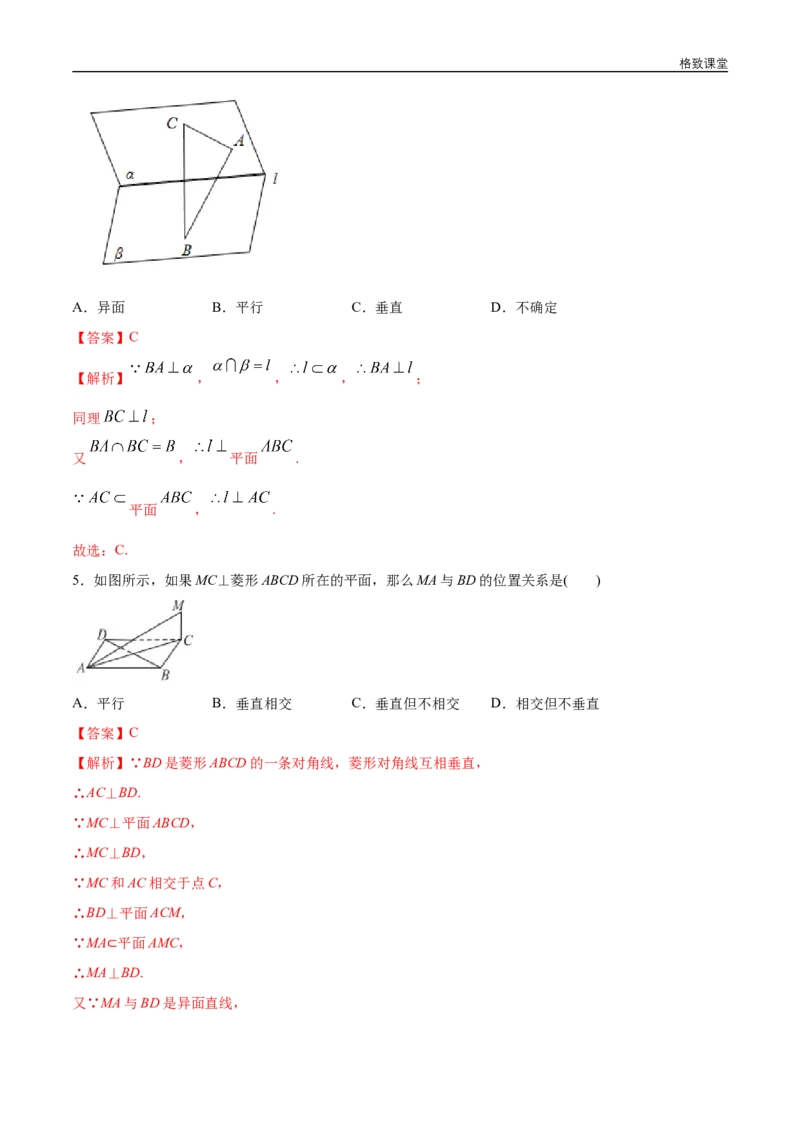
2.如图,点 ,点 ,点 , , 是 内异于 和 的动点,且 ,则动
点 在平面 内所组成的集合是( )
A.一条线段,但要去掉两个点 B.一个圆,但要去掉两个点
C.半圆 D.半圆,但要去掉两个点
【答案】B格致课堂
【解析】连接 , ,由于 , ,
所以 平面 , 平面
所以 ,说明动点 在以 为直径的圆上,
但不与点 重合.所以B正确
故选:B
3.在长方体 中,M,N分别为 ,AB的中点, ,则MN与平面 的
距离为( )
A.4 B. C.2 D.
【答案】C
【解析】如图,
BC ,又 平面 , 平面 .
1
∴MN与平面 的距离为N到面 的距离.又N到平面 的距离为 .
∴MN与平面 的距离为2.
故选:C
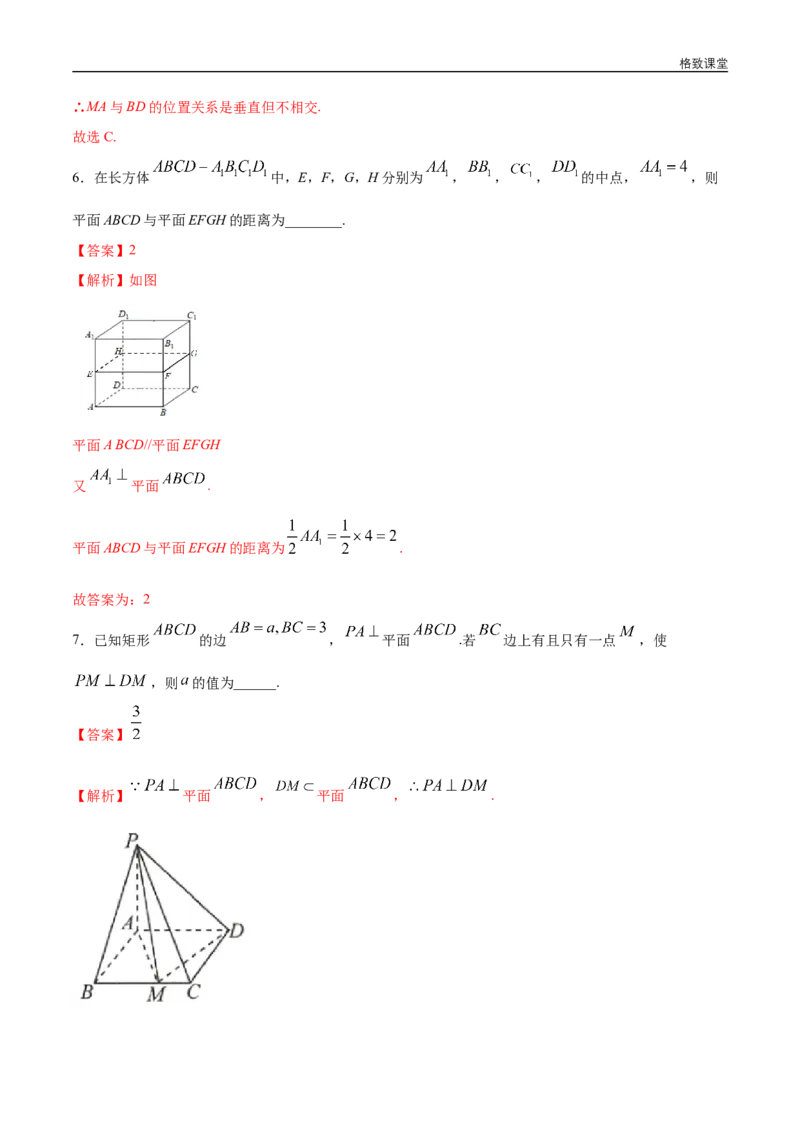
4.如图, ,点 ,点 ,且 , ,那么直线l与直线 的关系是
( )格致课堂
A.异面 B.平行 C.垂直 D.不确定
【答案】C
【解析】 , , , ;
同理 ;
又 , 平面 .
平面 , .
故选:C.
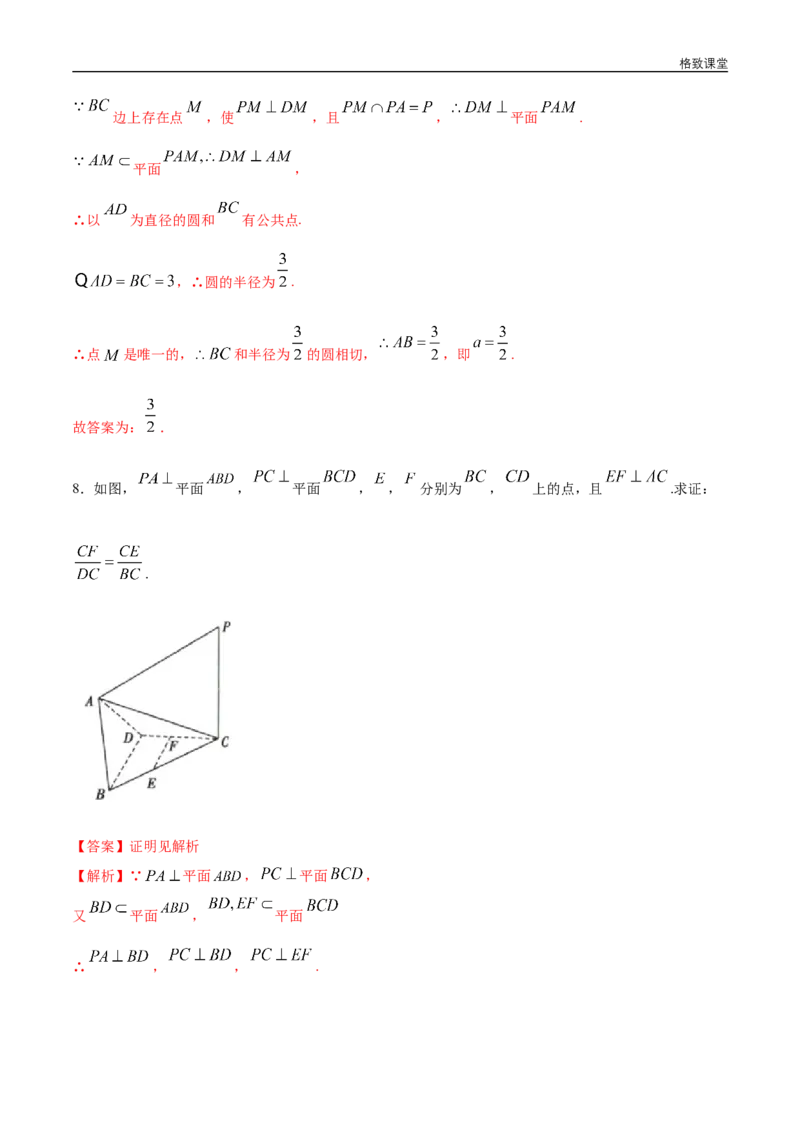
5.如图所示,如果MC⊥菱形ABCD所在的平面,那么MA与BD的位置关系是( )
A.平行 B.垂直相交 C.垂直但不相交 D.相交但不垂直
【答案】C
【解析】∵BD是菱形ABCD的一条对角线,菱形对角线互相垂直,
∴AC⊥BD.
∵MC⊥平面ABCD,
∴MC⊥BD,
∵MC和AC相交于点C,
∴BD⊥平面ACM,
∵MA 平面AMC,
∴MA⊂⊥BD.
又∵MA与BD是异面直线,格致课堂
∴MA与BD的位置关系是垂直但不相交.
故选C.
6.在长方体 中,E,F,G,H分别为 , , , 的中点, ,则
平面ABCD与平面EFGH的距离为________.
【答案】2
【解析】如图
平面A BCD//平面EFGH
又 平面 .
平面ABCD与平面EFGH的距离为 .
故答案为:2
7.已知矩形 的边 , 平面 .若 边上有且只有一点 ,使
,则 的值为______.
【答案】
【解析】 平面 , 平面 , .格致课堂
边上存在点 ,使 ,且 , 平面 .
平面 ,
∴以 为直径的圆和 有公共点.
,∴圆的半径为 .
∴点 是唯一的, 和半径为 的圆相切, ,即 .
故答案为: .
8.如图, 平面 , 平面 , , 分别为 , 上的点,且 .求证:
.
【答案】证明见解析
【解析】∵ 平面 , 平面 ,
又 平面 , 平面
∴ , , .格致课堂
又 , 平面
∴ 平面 .
又 , ,
平面 ∴ 平面 ,
∴ // ,∴ .
能力提升
9.如图所示,直线PA垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB
的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中正
确的是( )
A.①② B.①②③ C.① D.②③
【答案】B
【解析】对于①,∵PA⊥平面ABC,∴PA⊥BC.
∵AB为⊙O的直径,∴BC⊥AC,
又∵PA∩AC=A,∴BC⊥平面PAC,
又PC 平面PAC,∴BC⊥PC,对于②,∵点M为线段PB的中点,∴OM∥PA,
∵PA ⊂平面PAC,OM 平面PAC,
∴OM⊂∥平面PAC,对⊄于③,由①知BC⊥平面PAC,
∴线段BC的长即是点B到平面PAC的距离,故①②③都正确.
10.如图,在直角梯形 中, , , 、 分别是 、 的中点,将三角形
沿 折起,则下列说法正确的是______________.格致课堂
(1)不论 折至何位置(不在平面 内),都有 平面 ;
(2)不论 折至何位置,都有 ;
(3)不论 折至何位置(不在平面 内),都有 ;
(4)在折起过程中,一定存在某个位置,使 .
【答案】(1)(2)(4)
【解析】
折叠后如图,分别取 中点 ,连接 ,易知 是 的交点,因此 也是
中点,而 别是 的中点,
∴ , ,∴ 是平行四边形,∴ ,
平面 , 平面 ,∴ 平面 .(1)正确;
折叠过程中 保持不变,又 ,所以 平面 ,从而 ,格致课堂
所以 ,(2)正确;
若 ,则 共面,即 共面,从而直线 共面,这样 在平面 也
即在平面 内,矛盾,(3)错误;
当 时,又 ,而 ,∴ 平面 , 平面 ,所以
.(4)正确.
故答案为:(1)(2)(4).
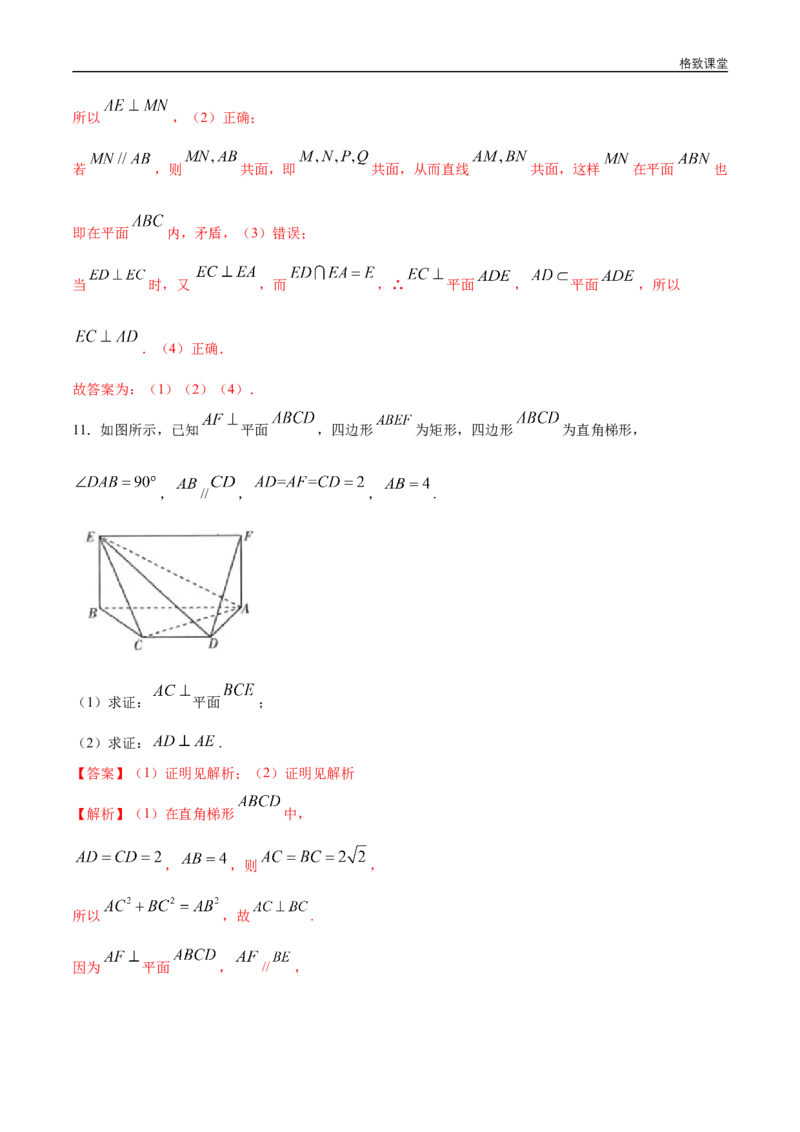
11.如图所示,已知 平面 ,四边形 为矩形,四边形 为直角梯形,
, // , , .
(1)求证: 平面 ;
(2)求证: .
【答案】(1)证明见解析;(2)证明见解析
【解析】(1)在直角梯形 中,
, ,则 ,
所以 ,故 .
因为 平面 , // ,格致课堂
所以 平面 ,所以 .
又 平面 , ,
所以 平面 .
(2)因为 平面 , 平面 ,
所以 ,又 ,所以 .
又 平面 , ,
所以 平面 .
又 平面 ,所以 .
素养达成
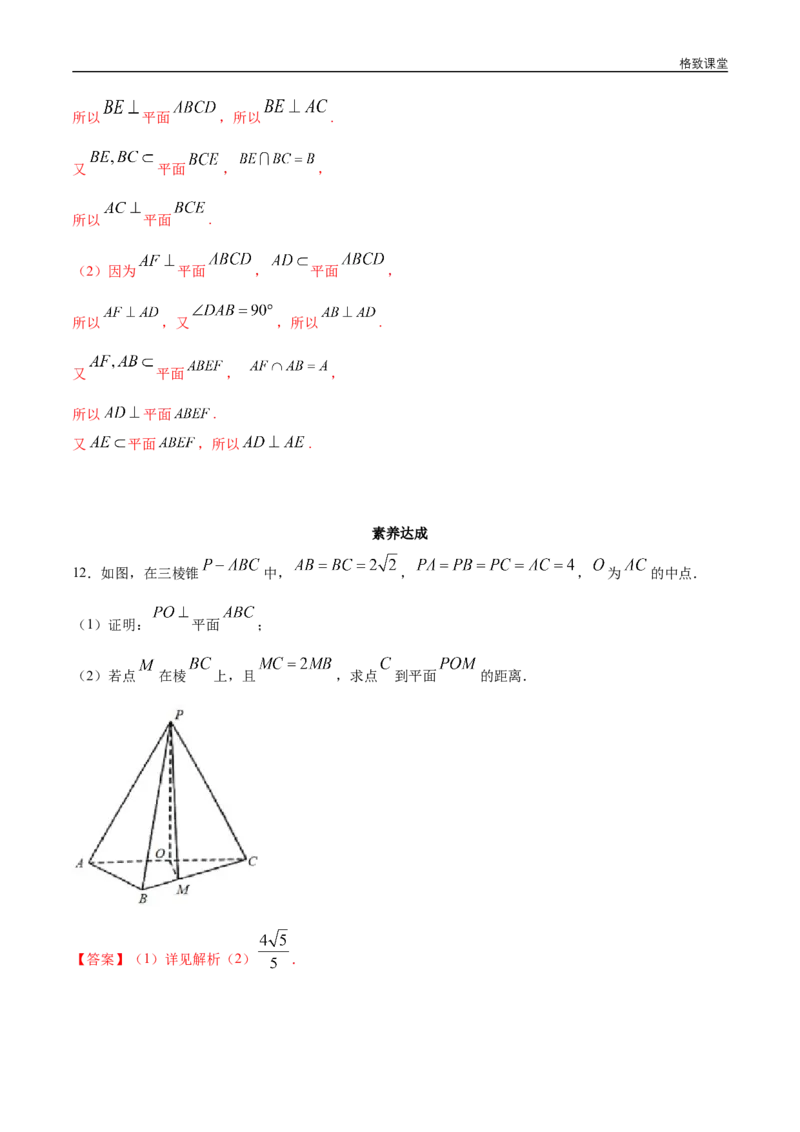
12.如图,在三棱锥 中, , , 为 的中点.
(1)证明: 平面 ;
(2)若点 在棱 上,且 ,求点 到平面 的距离.
【答案】(1)详见解析(2) .格致课堂
【解析】(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP= .
连结OB.因为AB=BC= ,所以△ABC为等腰直角三角形,且OB⊥AC,OB= =2.
由 知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.
由题设可知OC= =2,CM= = ,∠ACB=45°.
所以OM= ,CH= = .
所以点C到平面POM的距离为 .