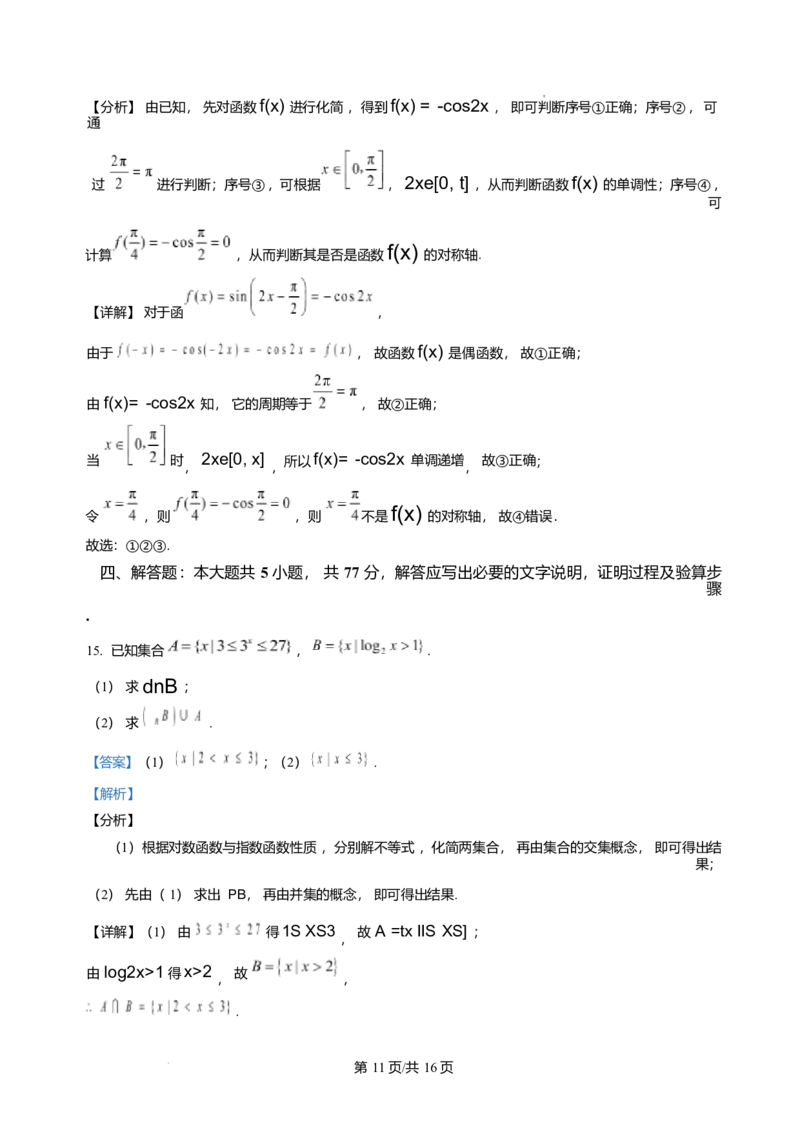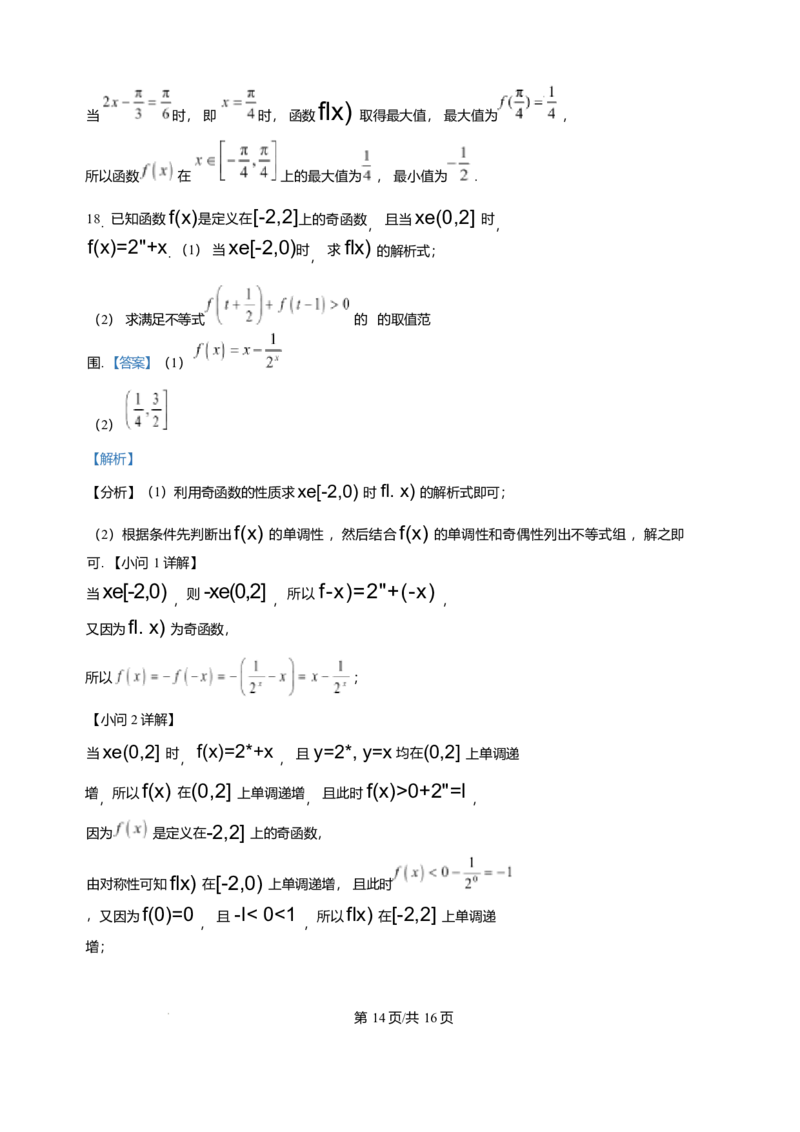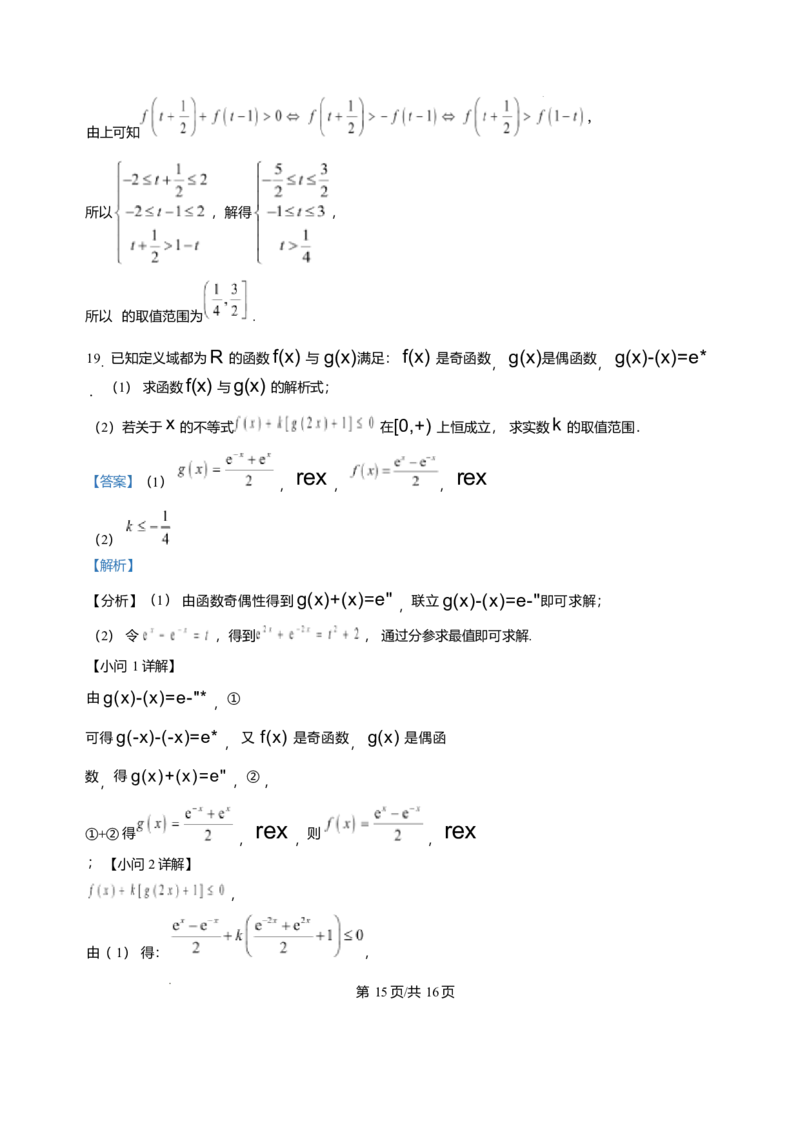文档内容
济南一中 2025 级高一上学期 1 月学情检测
数学试题
本试卷满分 150 分 考试时间 120 分钟
一 、单项选择题:本大题共 8 小题,每小题 5 分, 共 40 分,每小题只有一个选项符合题目
要求.
A门B=
1. 已知集合 ,则 ( )
A. B.
C. D.
2 . 若 sinf cosf <0) , 且 sinf-co sf>) , 则 是 ( )
A. 第—象限 角 B. 第二象限的角
C. 第三象限的角 D. 第四象限的角
3. 已知 , ,则 r 是 a 的 ( )
A 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
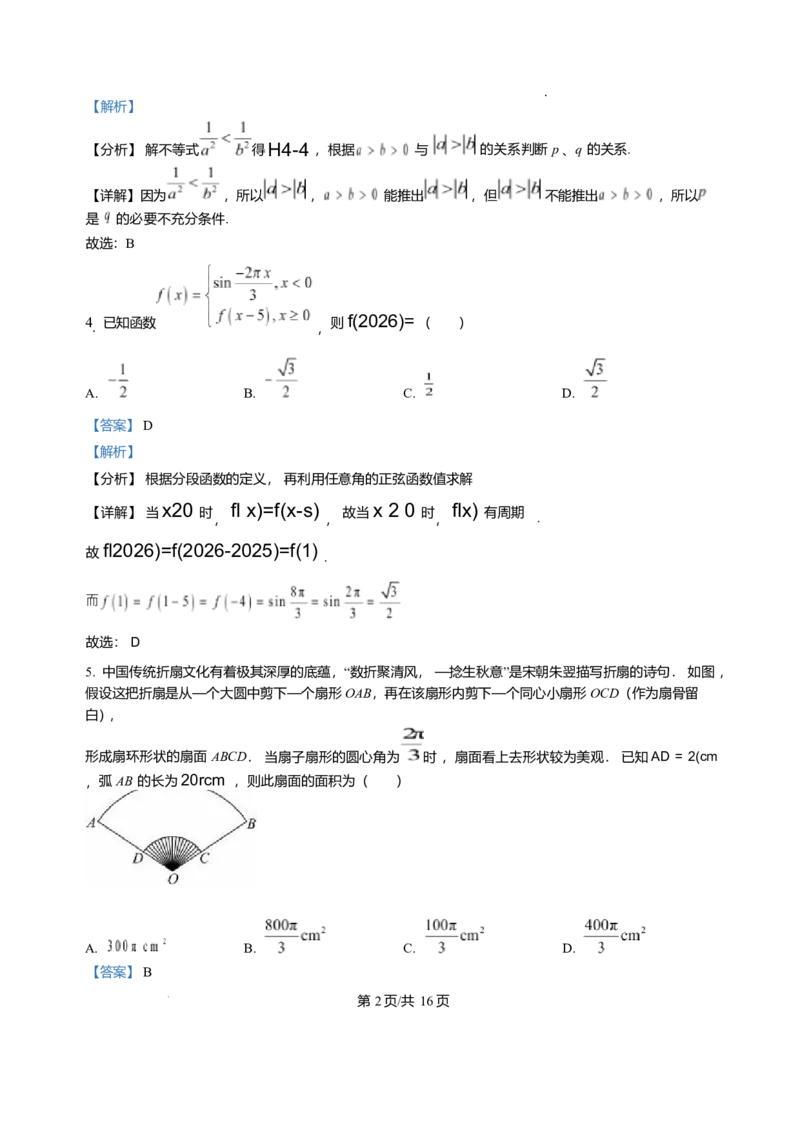
4 已知函数 则 f(2026)= ( )
,
A. B. C. D.
5. 中国传统折扇文化有着极其深厚的底蕴,“数折聚清风, —捻生秋意”是宋朝朱翌描写折扇的诗句. 如图 ,
假设这把折扇是从—个大圆中剪下—个扇形 OAB,再在该扇形内剪下—个同心小扇形 OCD(作为扇骨留
白),
形成扇环形状的扇面 ABCD. 当扇子扇形的圆心角为 时 ,扇面看上去形状较为美观. 已知AD = 2(cm
,弧 AB 的长为20rcm ,则此扇面的面积为 ( )
A. B. C. D.
第 1页/共 4页6. 设 , , c= ln5 ,则 e 、s 、 的大小关系是 ( )
A a> b>c B c>b>a C b >c>a D a>c>b
. . . .
7. 下列函数中最小正周期为 , 且在区间 上单调递增的是 ( )
A. y=sin x B. C. D.
F(x)=f(x)-b
8. 已知函数 ,若函数 有四个不同的零点
, 则 的取值范围是 ( )
A. B. C. D.
二 、多项选择题:本大题共 3 小题,每小题 6 分, 共 18 分,在每小题给出的选项中,有多
项符合题目要求,全对得 6 分, 部分选对的得部分分, 有选错的得 0 分.
9. 若角A,B,C 是 ABC 的三个内角 ,则下列等式中—定成立的是 ( )
A sin(A+B)=sin c B
. .
C. D. cos(2A+2B)=cos2c
R f(x) fl x+2)=-f(x) 0s xsl f(x)=x
10. 已知定义在 上的函数 满足:
,
当 时
, ,
且函数
f(x-1)
的图象关于点(1,0) 对称 ,则下列说法正确的是 ( )
A. f(x) 的图象关于直线t=2 对称
B. f(x) 是奇函数
C f(x+ 4)= f(x)
.
lgr- f(x)=)
D. 方程 有 4 个不相等的实根
11. 已知 , 其中 且 ,则 ( )
flx)
A. 偶函数
fx)
B. 的图象经过原点
·
第 2页/共 4页g(x)=f(x)-2
C . 函数 有—个零点
a>1 fx)=f1x:)
D. 当 时
,
若 且
,
则
三、填空题:本大题共 3 小题, 每小题 5 分, 共 15 分.
12. 已知函数y=log(x+3)-2 ( a >0 且 ) 的图象恒过定点坐标__________.
13. 已知 ue lu-al , 且 ,则 ______.
14. 已知函数 , 下列结论你认为正确的是______( 填序号)
flx)
①函数 是偶函数
f(x)
②函数 的最小正周期为
flx)
③函数 在区间 上单调递增
flx)
④函数 的图像关于直线 对称
四、解答题:本大题共 5 小题, 共 77 分,解答应写出必要的文字说明,证明过程及验算步
骤
.
15. 已知集合 , .
dnB
(1) 求 ;
(2) 求 .
16. 已知函数
x
(1)若 为第二象限角 ,试化简f(x) 表达式;
(2)若 , 计算sin r(sin x+cos x) 的值 .
17. 已知函数 .
flx) flx) [0,r
(1) 求 的最小正周期及 在区间 内的单调递增区间;
第 3页/共 4页flx)
(2) 当 时, 求 的最大值及最小值, 并求出相应的 的取值.
[-2,2] xe(0,2] fl x)=2"+x
18. 已知函数 是定义在 上的奇函数 , 且当 时 , .
xel-2,0) flx)
(1) 当 时 求 解析式;
,
(2) 求满足不等式 的 的取值范围.
19. 已知定义域都为R 的函数 f(x) 与 g(x) 满足: f(x) 是奇函数
,
g(x) 是偶函数
,
g(x)-
(x)=e* (1) 求函数 f(x) 与 g(x) 的解析式;
.
(2)若关于 x 的不等式 在[0,+x) 上恒成立, 求实数 k 的取值范围.
第 4页/共 4页济南一中 2025 级高一上学期 1 月学情检测
数学试题
本试卷满分 150 分 考试时间 120 分钟
一 、单项选择题:本大题共 8 小题,每小题 5 分, 共 40 分,每小题只有一个选项符合题目
要求.
A门B=
1. 已知集合 ,则 ( )
A. B.
C. D.
【答案】 C
【解析】
【分析】 先求得集合 , 再根据交集的定义与运算求出结果.
【详解】 由集合 ,
所以 ,
故选:C.
2 . 若 sinf cos fk0) , 且 sinf-co sf>) , 则 是 ( )
A. 第—象限的角 B. 第二象限的角
C. 第三象限的角 D. 第四象限的角
【答案】 B
【解析】
【分析】 判断出角 的正余弦的正负, 进而可得答案.
【详解】 由 ,得 ,
所以角 位于第二象限的角.
故选:B
3. 已知 , ,则 是 的 ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】 B
第 1页/共 16页·
【解析】
【分析】 解不等式 得H4-4 ,根据 与 的关系判断 p 、q 的关系.
【详解】因为 ,所以 , 能推出 ,但 不能推出 ,所以
是 的必要不充分条件.
故选:B
4 . 已知函数 , 则 f(2026)= ( )
A. B. C. D.
【答案】 D
【解析】
【分析】 根据分段函数的定义, 再利用任意角的正弦函数值求解
x20 fl x)=f(x-s) x 2 0 flx)
【详解】 当 时 , , 故当 时 , 有周期 .
fl2026)=f(2026-2025)=f(1)
故 .
⽽
故选: D
5. 中国传统折扇文化有着极其深厚的底蕴,“数折聚清风, —捻生秋意”是宋朝朱翌描写折扇的诗句. 如图 ,
假设这把折扇是从—个大圆中剪下—个扇形 OAB,再在该扇形内剪下—个同心小扇形 OCD(作为扇骨留
白),
形成扇环形状的扇面 ABCD. 当扇子扇形的圆心角为 时 ,扇面看上去形状较为美观. 已知AD = 2(cm
,弧 AB 的长为20rcm ,则此扇面的面积为 ( )
A. B. C. D.
【答案】 B
第 2页/共 16页·
【解析】
【分析】 先通过弧长公式求出大扇形半径 0A , 再结合AD 的长度得到小扇形半径0D , 最后利用扇形
面积公式计算两个扇形的面积差 ,得到扇面面积.
【详解】 设0A=Rcm 因为圆心角 弧 AB 的长为ly g=20cm
, , ,
代入弧长公式 可得 ,解得 R=30 .
所以0D = 30-20=10
.
由扇形面积公式 可得,
,
,
所以此扇面的面积
.
故选:B
6. 设 , , c= ln5 ,则 o 、s 、 的大小关系是 ( )
A a> b>c B c>b>a C b >c>a D a>c>b
. . . .
【答案】 B
【解析】
【分析】 利用指数函数和对数函数的单调性比较a 、b 、 三个数与 和 的大小关系 ,利用换底公式和
不等式的基本性质可得出 、 的大小关系, 进而可得出这三个数的大小关系.
(< a l ne=1 .
第 3页/共 16页.
c>b>a
因此 , .
故选:B.
【点睛】 本题考查指数式和对数式的大小比较, —般利用指数函数和对数函数的单调性, 结合中间值法
来比较 ,考查推理能力 ,属于中等题.
7. 下列函数中最小正周期为 , 且在区间 上单调递增的是 ( )
A y=sin x B C D
. . . .
【答案】 B
【解析】
【分析】利用函数的周期排除 A ,C 两项 ,对于 B ,D 两项 ,两函数的图象可通过正弦函数与余弦函数的
图象翻折得到, 结合图象即可判断.
【详解】 依题意 ,对于 A ,C, 两函数的最小正周期都是 21 , 故 A ,C 均不正
y=inN
确;对于 B, 因函数 可由正弦函数的图象 ,将 轴下方部分向上翻折
得到,
r - a y-hi nl
故其最小正周期为正弦函数的周期 的—半, 即 , 且函数 在 上单调递增, 故
B 正确;
y=l cos
对于 D, 因函数 可由余弦函数的图象 ,将 轴下方部分向上翻折得到,
故其最小正周期为余弦函数的周期 的—半 ,即 ,且函数 在 上单调递减 ,故 D
不正确.
故选:B.
F(x)=f(x)-b
8. 已知函数 ,若函数 有四个不同的零点
, 则 的取值范围是 ( )
A B. C. D.
【答案】 C
【解析】
·
第 4页/共 16页·
【分析】
根据题意得到 , , 再对所求目标式子进行化简 ,利用对勾函数的单调性, 得到所求
范围.
F(xt)=f(x)-b (x0
当 时, ;结合奇函数性质与周期性, 可画出 在 上的图象,
y= lgr 在x=10 时 lg10=1 ;x>10 时 lgx> l
, , ,
flx) I-.1] xe(0,10)
而 的值域为 , 因此只需考虑 的区间, 逐—分析区间内交点:
y=x
: 与 无交点;
(1,3] : fl. x) 图象与 有 1 个交点;
flx) y=lg s
: 图象与 有 1 个交点;
15,71 : flx) 图象与 有 1 个交点;
(7,9 : fl. x) 图象与y=lg s 有 1 个交
点; (9,10j : fl. x) 图象与 有 1 个
交点;因此总计 5 个不相等的实根 ,D 错误.
故选:BC
JI X)=lo'-ll
11. 已知
,
其中 且
,
则 ( )
flx)
A. 为偶函数
f(x)
B. 的图象经过原点
g(x)=f(x)-2
C . 函数 有—个零点
D. 当 a>1 时 ,若 且 ,则
【答案】 BCD
【解析】
f(0)=0 gl x)=0
【分析】 A 利用偶函数的定义即可判断;B 由 可判断;C 令 ,解方程即可判断;D 画
出
第 8页/共 16页的图象 ,令 l'-Il-k 解方程求出x1, x2 , 结合对数运算及对数函数的性质即可判断.
R flx)
【详解】 A, 函数 的定义域为 , 与 不恒相等, 故 不是偶函数,
故 A错误;
f10)=o"-I=0 flx)
B 所以 的图象经过原点 故 B 正确;
, , ,
gl x)=0 u'-I - -2 a' -I=
C 令 即 即 所以 或
, , , ,
2 当 时 a' = -I 因为a' >0 故无解
, , , , ,
当a' -I= 2 时 解得x=log。3
, ,
g(x)=fl x)-2
所以函数 只有—个零点, 故 C 正确;
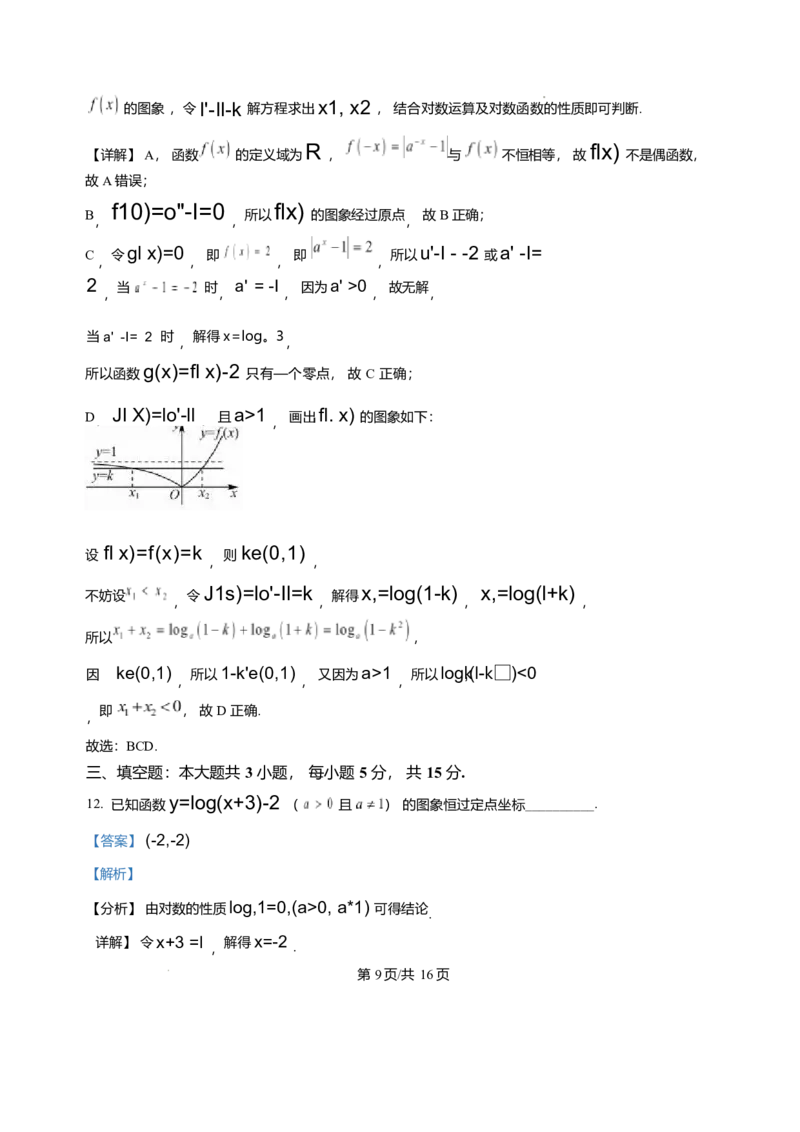
JI X)=lo'-ll a>1 fl. x)
D 且 画出 的图象如下:
, , ,
fl x)=f(x)=k ke(0,1)
设 则
, ,
J1s)=lo'-Il=k x,=log(1-k) x,=log(l+k)
不妨设 令 解得
, , , ,
所以 ,
因 ke(0,1) 所以1-k'e(0,1) 又因为a>1 所以log,k⃞(l-k⃞(cid:2))<0
, , ,
即 , 故 D 正确.
,
故选:BCD.
三、填空题:本大题共 3 小题, 每小题 5 分, 共 15 分.
y=log(x+3)-2
12. 已知函数 ( 且 ) 的图象恒过定点坐标__________.
【答案】 (-2,-2)
【解析】
【分析】 由对数的性质log,1=0,(a>0, a*1) 可得结论.
详解】 令x+3 =l , 解得x=-2 .
第 9页/共 16页当 x=-2 时 , y=log,1-2=0-2=-2 .
即函数恒过定点(-2,-2) .
故答案为: (-2,-2) .
13. 已知 , 且 ,则 ______.
【答案】
【解析】
【分析】 由 两边平方可求 , 判断 的象限, 再结合同角关系求结
论.
【详解】 由 两边平方可得
,⼜ ,
ae(0,)
所以 又
, ,
所以 , 故 ,
⼜ ,
所以 .
故答案为: .
14. 已知函数 , 下列结论你认为正确的是______( 填序号)
①函数f(x) 是偶函数
f(x)
②函数 的最小正周期为
flx)
③函数 在区间 上单调递增
flx)
④函数 的图像关于直线 对称
【答案】
①②③ 【解
析】
第 10页/共 16页【分析】 由已知, 先对函数f(x) 进行化简 ,得到f(x) = -cos2x , 即可判断序号①正确;序号② , 可
通
2xe[0, t] f(x)
过 进行判断;序号③ , 可根据 , ,从而判断函数 的单调性;序号④ ,
可
f(x)
计算 ,从而判断其是否是函数 的对称轴.
【详解】 对于函 ,
由于 , 故函数f(x) 是偶函数, 故①正确;
由 f(x)= -cos2x 知, 它的周期等于 , 故②正确;
当 时 2xe[0, x] 所以 f(x)= -cos2x 单调递增 故③正确;
, , ,
f(x)
令 ,则 ,则 不是 的对称轴, 故④错误.
故选:①②③.
四、解答题:本大题共 5 小题, 共 77 分,解答应写出必要的文字说明,证明过程及验算步
骤
.
15. 已知集合 , .
(1) 求 dnB ;
(2) 求 .
【答案】(1) ;(2) .
【解析】
【分析】
(1)根据对数函数与指数函数性质 ,分别解不等式 ,化简两集合, 再由集合的交集概念, 即可得出结
果;
(2) 先由( 1) 求出 PB, 再由并集的概念, 即可得出结果.
【详解】(1) 由 得1S XS3 故 A =tx IIS XS] ;
,
由 log2x>1得 x>2 故
, ,
.
第 11页/共 16页XB=txl xs2
(2) 由 得
,
.
【点睛】 本题主要考查集合的交集并集和补集运算 ,熟记概念即可, 涉及指数与对数不等式 ,属于基础
题型.
16. 已知函数
x f(x)
(1)若 为第二象限角 ,试化简 表达式;
(2)若 ,计算 的值.
【答案】(1) j(x)= tan x ;
(2) 答案见解析.
【解析】
【分析】(1)根据给定条件 ,利用诱导公式及同角公式化简即得.
(2) 由( 1) 的信息 ,利用正余弦齐次式法分类计算即得.
【小问 1 详解】
由 x 为第二象限角 ,得cos x<0 ,
所以函数 .
【小问 2 详解】
由( 1) 知 而 则 sin x>(
, , , ,
cos x<) :
当 , 即 第二象限角时, ,
;
当cos x>0 , 即 是第—象限角时, ,
第 12页/共 16页.
17. 已知函数 .
flx)
(1) 求 的最小正周期及 在区间 内的单调递增区间;
fl. x) :
(2) 当 时, 求 的最大值及最小值, 并求出相应的 的取
值. 【答案】(1) 最小正周期为 ;
-
(2) 时, 最大值为 ; 时, 最小值为 .
【解析】
flx)
【 分 析 】( 1) 利 用 正 弦 型 函 数 最 小 正 周 期 的 计 算 公 式 , 求 得 函 数 的 最 小 正 周 期 ,
根 据
, 结合正弦函数的单调性, 进而求得 的单调递增区间;
(2)根据 , 求得 , 结合正弦函数的性质可求答
案. 【小问 1 详解】
fl. x)
由函数 , 可得函数 的最小正周期为 ,
由 , 可得 ,
令 , 可得 ;令 , 可得 ,
所以函数 的单调递增区间为 .
【小问 2 详解】
由 , 可得 ,
flx)
当 时, 即 时, 函数 取得最小值, 最小值为 ;
·
第 13页/共 16页flx)
当 时, 即 时, 函数 取得最大值, 最大值为 ,
所以函数 在 上的最大值为 , 最小值为 .
f(x) [-2,2] xe(0,2]
18. 已知函数 是定义在 上的奇函数
,
且当 时
,
f(x)=2"+x xe[-2,0) flx)
. (1) 当 时 求 的解析式;
,
(2) 求满足不等式 的 的取值范
围. 【答案】(1)
(2)
【解析】
【分析】(1)利用奇函数的性质求xe[-2,0) 时 fl. x) 的解析式即可;
f(x) f(x)
(2)根据条件先判断出 的单调性 ,然后结合 的单调性和奇偶性列出不等式组 ,解之即
可. 【小问 1 详解】
xe[-2,0) -xe(0,2] f-x)=2"+(-x)
当 则 所以
, , ,
fl. x)
又因为 为奇函数,
所以 ;
【小问 2 详解】
xe(0,2] f(x)=2*+x y=2*, y=x (0,2]
当 时 且 均在 上单调递
, ,
f(x) (0,2] f(x)>0+2"=l
增 所以 在 上单调递增 且此时
, , ,
因为 是定义在-2,2] 上的奇函数,
flx) [-2,0)
由对称性可知 在 上单调递增, 且此时
f(0)=0 -I< 0<1 flx) [-2,2]
,又因为 且 所以 在 上单调递
, ,
增;
第 14页/共 16页由上可知
所以 ,解得 ,
所以 的取值范围为 .
19. 已知定义域都为 R 的函数 f(x) 与 g(x) 满足: f(x) 是奇函数
,
g(x) 是偶函数
,
g(x)-(x)=e*
f(x) g(x)
(1) 求函数 与 的解析式;
.
(2)若关于 x 的不等式 在 [0,+) 上恒成立, 求实数 k 的取值范围.
rex rex
【答案】(1)
, , ,
(2)
【解析】
【分析】(1) 由函数奇偶性得到 g(x)+(x)=e" 联立g(x)-(x)=e-"即可求解;
,
(2) 令 ,得到 , 通过分参求最值即可求解.
【小问 1 详解】
由g(x)-(x)=e-"* ①
,
可得g(-x)-(-x)=e* 又 f(x) 是奇函数 g(x) 是偶函
, ,
数 得g(x)+(x)=e" ②
, , ,
rex rex
①+②得 则
, , ,
; 【小问 2 详解】
,
由( 1) 得: ,
·
第 15页/共 16页令e'- e"'= i 又 y= t ' - ' 在[0,+n) 单调递增 所以 t20
, , ,
则 ,
得: 在[0,+n) 恒成立,
i-o
分参可得: , 当 时,
t>0
,当 时
,
,
t=2
因为 , 当且仅当 时取等号, 的最小值为 ,
综上当 时, 的最小值为 ,
所以 .
第 16页/共 16页