文档内容
高一上册数学期中模拟卷02
本试卷共4页,22小题,满分150分,考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合 , ,则 ( )
A. B. C. D.
2.已知函数 若 ,且 ,则 ( )
A. B.0 C.1 D.2
3.二次不等式 的解集是 ,则 的值为( )
A. B. C. D.
4.函数 的图象大致为( )
A. B.
C. D.
5.已知集合 , ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.若函数 在 上是减函数,则实数m的取值范围是( )A. B. C. D.
7.已知正实数a、b满足 ,若 的最小值为4,则实数m的取值范围是( )
A. B. C. D.
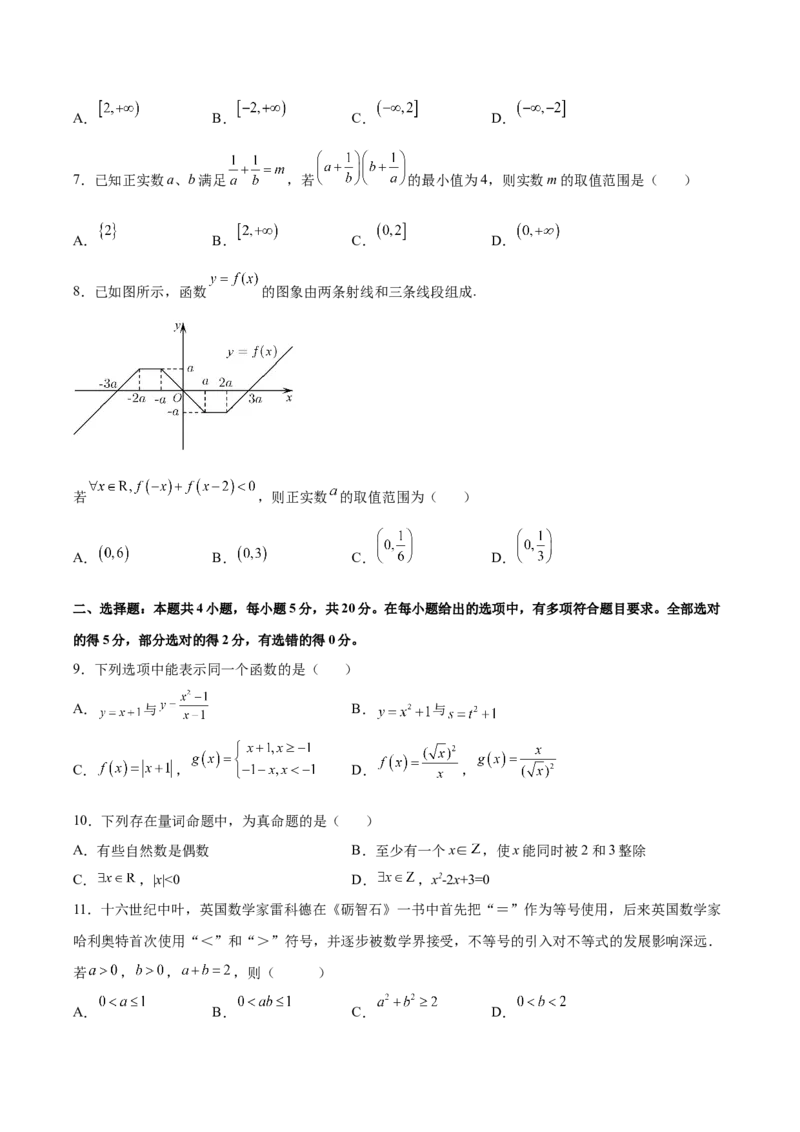
8.已如图所示,函数 的图象由两条射线和三条线段组成.
若 ,则正实数 的取值范围为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对
的得5分,部分选对的得2分,有选错的得0分。
9.下列选项中能表示同一个函数的是( )
A. 与 B. 与
C. , D. ,
10.下列存在量词命题中,为真命题的是( )
A.有些自然数是偶数 B.至少有一个x∈ ,使x能同时被2和3整除
C. ,|x|<0 D. ,x2-2x+3=0
11.十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家
哈利奥特首次使用“<”和“>”符号,并逐步被数学界接受,不等号的引入对不等式的发展影响深远.
若 , , ,则( )
A. B. C. D.12.已知 是定义在R上的不恒为零的函数,对于任意a, 都满足 ,则下述正
确的是( )
A. B. C. 是奇函数 D.若 ,则
三.填空题 本题共4小题,每小题5分,共20分
13.已知 , ,则 的取值范围是_________
14.某年级先后举办了数学、历史、音乐讲座,其中有75人听了数学讲座,68人听了历史讲座,61人听
了音乐讲座,17人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲
座,还有6人听了全部讲座,则听讲座人数为__________.
15.已知幂函数 的图像关于y轴对称,且在 上是减函数,实数 满足
,则 的取值范围是_____.
16.已知函数 的定义域为 ,则当 ___________时, 取得最小值,且最小值为
___________.
四.解答题:本题共6小题,17题10分,剩下每题12分。共70分,解答应写出文字说明、证明过程或演算步
骤
17.已知函数 .
(1)若 ,求实数 的值;
(2)若 , 恒成立,求:实数 的取值范围.
18.设集合 ,集合 .
(1)若 ,求 , ;
(2)设命题 ,命题 ,若 是 成立的必要不充分条件,求实数 的取值范围.19.已知函数 , .
(1)当 时,写出函数 的单调区间和值域(不用写过程);
(2)求 的最小值 的表达式.
20.已知函数 .
(1)求函数 的解析式;
(2)设 ,若存在 使 成立,求实数 的取值范围.
.
21.2020 年初至今,新冠肺炎疫情袭击全球,对人民生命安全和生产生活造成严重影响. 在党和政府强有
力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降
对企业和民众带来的损失. 为降低疫情影响,某厂家拟在2022年举行某产品的促销活动,经调查测算,该
产品的年销售量(即该厂的年产量) x万件与年促销费用m万元(m≥0)满足 x= 4− . 已知生产该产品的固
定成本为 8万元,生产成本为16万元 / 万件,厂家将产品的销售价格定为 万元 / 万件 (产品年平
均成本)的1.5倍.
(1)将2022年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2022年的促销费用投入多少万元时,厂家的利润最大?
22.函数 的定义域为R,若存在常数 ,使得 对一切实数x均成立,则称
为“圆锥托底型”函数.
(1)判断函数 , 是否为“圆锥托底型”函数?并说明理由;
(2)若 是“圆锥托底型”函数,求出M的最大值;(3)问实数k、b满足什么条件, 是“圆锥托底型”函数.