文档内容
期中测试卷 01
(本卷满分150分,考试时间120分钟)
(人教A版2019)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符
合题目要求的.
1.复数 在复平面内对应的点位于( )。
A、第一象限
B、第二象限
C、第三象限
D、第四象限
【答案】B
【解析】 ,在复平面对应的点的坐标为 ,位于第二象限,故选B。
2.若复数 ( 为虚数单位),则 ( )。
A、
B、
C、
D、
【答案】A
【解析】 ,∴ ,故选A。
3.已知向量 , ,且 与 平行,则 ( )。
A、
B、
C、
D、
【答案】A
【解析】∵ 、 ,且 与 平行,∴ ,解得 ,故选A。
4.已知 、 、 是三条不同的直线, 、 是两个不同的平面,则下面说法中正确的是( )。
A、若 , ,且 , ,则
B、若 , ,且 ,则
C、若 且 ,则
D、若 , ,且 , ,则
【答案】D
【解析】A选项错,∵ 、 两条直线的位置关系不确定,
∴只有 、 相交时才能得到 ,
B选项错,如图所示,把 看作 , 看作 ,
平面 看作 ,平面 看作 ,此时 ,
C选项错,若 且 ,则 或 在 内,
D选项对,∵ , ,∴ ,若 , ,则 ,
故选D。
5.如图所示,已知一圆台上底面半径为 ,下底面半径为 ,母线 长为 ,其中 在上
底面上, 在下底面上,从 的中点 处拉一条绳子,绕圆台的侧面转一周达到 点,则这条绳子的长
度最短为( )。
A、
B、
C、
D、
【答案】C
【解析】画图,则设 ,圆心角为 ,则 ,
,解得 , ,
则 , , ,故选C。
6 . 已 知 中 , , , , 为 所 在 平 面 内 一 点 , 且 满 足
,则 的值为( )。
A、
B、
C、
D、
【答案】B
【解析】∵ ,∴ ,∴ ,∴ ,故选B。
7.平行四边形 中, ,且 ,沿 将四边形折起成平面 平面 ,
则三棱锥 外接球的表面积为( )。
A、
B、
C、
D、
【答案】C
【解析】将平面 平面 ,
又∵平面 平面 , 平面 ,
,∴ 平面 ,
∵四边形 为平行四边形,∴ ,
同理 平面 ,∴ 、 均为 ,
设 中点为 ,连 、 ,
则 , 为三棱锥 外接球半径,
则 , ,
则 ,故三棱锥 外接球的表面积为 ,故选C。
8.如图所示,三棱锥 中, 、 、 、 、 , 是 的中点,
,则三棱锥 的体积为( )。
A、
B、
C、
D、
【答案】D
【解析】由 、 、 可知 ,
∴ 为直角三角形,∴ ,
由 、 、 可知 ,
∴ 为直角三角形,∴ ,
又 , 平面 , 平面 ,
∴ 平面 ,由 是 的中点得 ,,
∵ ,∴ 为直角三角形, ,
∴ ,
又 , ,∴ ,即 为直角三角形, ,
∴ ,
∴ ,故选D。
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,
全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列说法中错误的是( )。
A、若 、 、 ,则
B、若 且 ,则
C、若 、 非零向量且 ,则
D、若 ,则有且只有一个实数 ,使得
【答案】ABD
【解析】A选项,当 、 中至少有一个 时, 与 可能不平行,错,
B选项,由 且 ,可得 或 ,错,
C选项, ,则两边平方化简可得 ,∴ ,对,
D选项,根据向量共线基本定理可知当 为零向量时不成立,错,
故选ABD。
10.下列四个命题中是真命题的是( )。
A、若复数 满足 ,则
B、若复数 满足 ,则
C、若复数 满足 ,则
D、若复数 、 满足 ,则
【答案】BC
【解析】A选项, , , ,则A是假命题,
具体做:设 ( ),则 ,则 或 ,
当 、 时 为纯虚数,当 、 时 为纯实数,
B选项,一个数的平方小于 ,则这个数一定是虚数,而且还是纯虚数,则B是假命题,具体做:设 ( ),则 ,则 且 ,
则 时 可取,则 时 不可取,
则 , , , 为纯虚数,
C选项, ,则 ,又 恒成立,∴ ,∴ ,则C是真命题,
具体做:设 ( ),则 ,
则 且 ,则 ,
D选项, 、 , , ,则D是假命题,
具体做:设 ( ), ( ),
则 ,
则 ,解有很多种可能,当 且 时符合条件,
此时 、 , 、 , 不一定成立,
故选BC。
11.已知四面体 是球 的内接四面体,且 是球 的一条直径, , ,则下面结论
正确的是( )。
A、球 的表面积为
B、 上存在一点 ,使得
C、若 为 的中点,则
D、四面体 体积的最大值为
【答案】ACD
【 解 析 】 ∵ 是 球 的 一 条 直 径 , ∴ , , ∴
,
球 的半径为 ,球 的表面积为 ,A正确,
∵ 与平面 相交, 上找不到一点 ,使得 ,B错误,
连接 、 ,∵ , 为 的中点,∴ ,C正确,
易知点 到平面 的距离的最大值为球的半径 ,
∴四面体 体积的最大值为: ,D正确,
故选ACD。
12.如图所示,正方体 的棱长为 , 、 分别是棱 、 的中点,过直线 、
的平面分别与棱 、 交于 、 ,设 , ,则下列命题中正确的是( )。
A、平面 平面B、当且仅当 时,四边形 的面积最小
C、四边形 周长 是单调函数
D、四棱锥 的体积 为常函数
【答案】ABD
【解析】A选项,∵ , , ,∴ ,∴ 平面 ,
又∵ 平面 ,∴平面 平面 ,A对,
B选项,∵四边形 为菱形,∴ ,
又 ,要使四边形 的面积最小,只需 最小,
则当且仅当 时,四边形 的面积最小,B对,
C选项,∵ , ,
∴ 在 上不是单调函数,C错,
D选项, ,
,点 到平面 的距离为 , ,
又 ,点 到平面 的距离为 , ,
∴ 为常函数,D对,
故选ABD。
三、填空题:本题共4小题,每小题5分,共20分.
13.设 是虚数单位,若复数 ( )是纯虚数,则 。
【答案】
【解析】 ,
∵复数 ( )是纯虚数,∴ ,且 ,∴ 。
14.古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑上刻着他认为最满意的一个
数学发现。如图,一个“圆柱容球”的几何图形,即圆柱容器里放了一个球,该球顶天立地,四周碰边,
在该图中,球的体积是圆柱体积的 ,并且球的表面积也是圆柱表面积的 ,若圆柱的表面积是 ,现
在向圆柱和球的缝隙里注水,则最多可以注入的水的体积为 。【答案】
【解析】设球的半径为 ,则由题意可得球的表面积为 ,∴ ,
∴圆柱的底面半径为 ,高为 ,∴最多可以注入的水的体积为 。
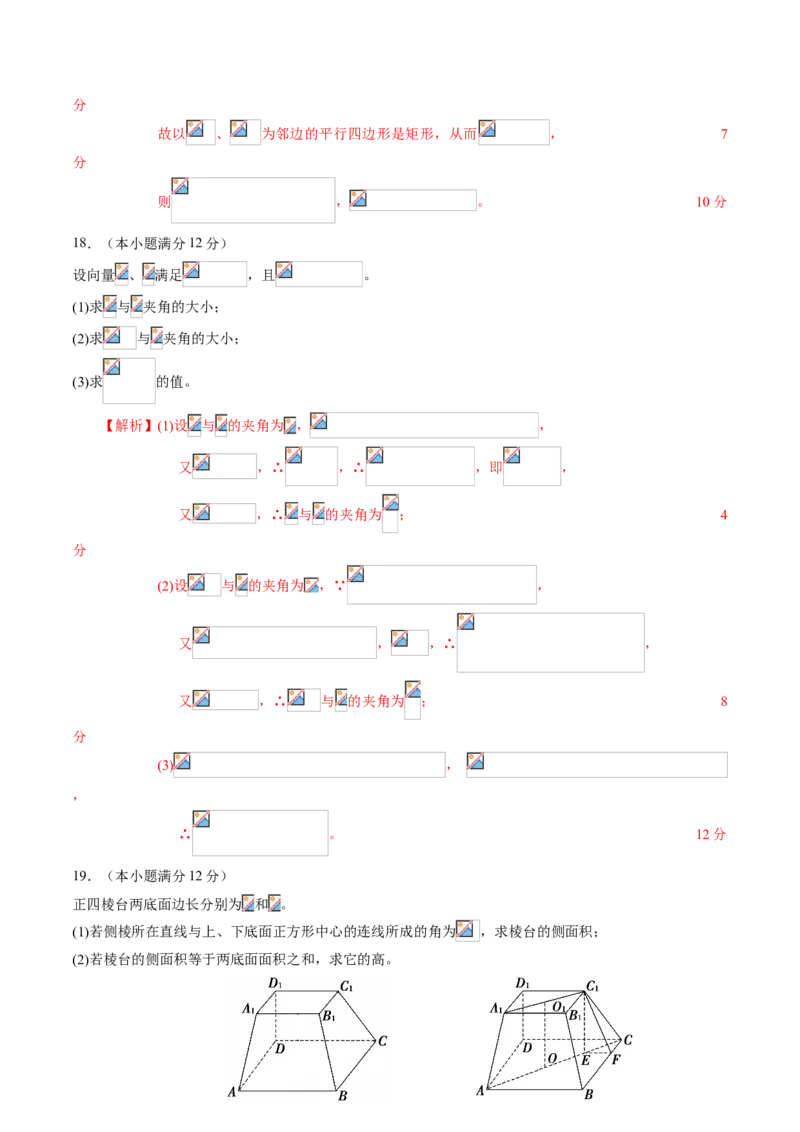
15.已知在边长为 的正三角形 中, 、 分别为边 、 上的动点,且 ,则
的最大值为 。
【答案】
【解析】如图建系,则 、 、 ,
则 , ,设 ( ),
则 ( ),则 , ,
∴ , ,
∴ ,
当 时 取最大值 。
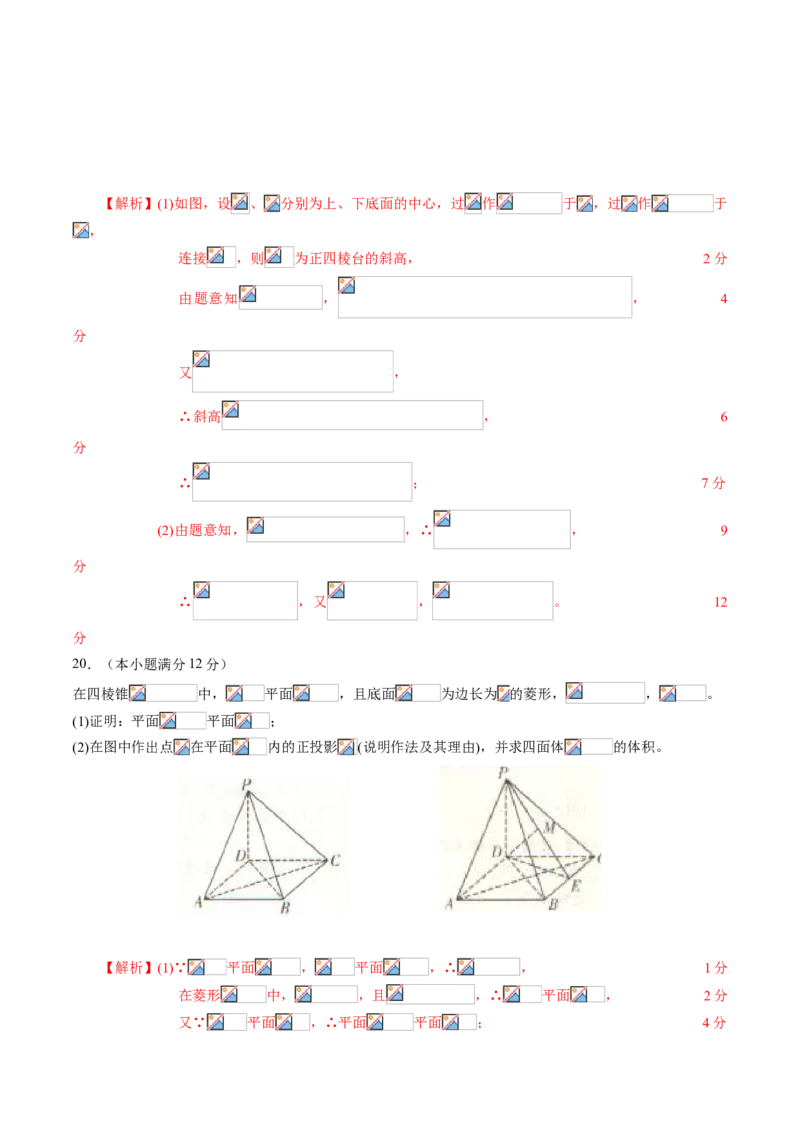
16.连接正方体相邻各面的中心(中心是指正方形的两条对角线的交点)后所得到了一个几何体,设正方体
的棱长为 ,则该几何体的表面积为 ,该几何体的体积为 。(本题第一空2分,第二空3分)
【答案】
【解析】这正八面体每个面是全等的正三角形,
, ,
∵ , , ,
∴ 。
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知复数 、 满足 、 ,且 ,求 与 的值。
【解析】设复数 、 在复平面上对应的点为 、 ,由于 , 2
分
故 , 4分
故以 、 为邻边的平行四边形是矩形,从而 , 7
分
则 , 。 10分
18.(本小题满分12分)
设向量 、 满足 ,且 。
(1)求 与 夹角的大小;
(2)求 与 夹角的大小;
(3)求 的值。
【解析】(1)设 与 的夹角为 , ,
又 ,∴ ,∴ ,即 ,
又 ,∴ 与 的夹角为 ; 4
分
(2)设 与 的夹角为 ,∵ ,
又 , ,∴ ,
又 ,∴ 与 的夹角为 ; 8
分
(3) ,
,
∴ 。 12分
19.(本小题满分12分)
正四棱台两底面边长分别为 和 。
(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为 ,求棱台的侧面积;
(2)若棱台的侧面积等于两底面面积之和,求它的高。【解析】(1)如图,设 、 分别为上、下底面的中心,过 作 于 ,过 作 于
,
连接 ,则 为正四棱台的斜高, 2分
由题意知 , , 4
分
又 ,
∴斜高 , 6
分
∴ ; 7分
(2)由题意知, ,∴ , 9
分
∴ ,又 , 。 12
分
20.(本小题满分12分)
在四棱锥 中, 平面 ,且底面 为边长为 的菱形, , 。
(1)证明:平面 平面 ;
(2)在图中作出点 在平面 内的正投影 (说明作法及其理由),并求四面体 的体积。
【解析】(1)∵ 平面 , 平面 ,∴ , 1分
在菱形 中, ,且 ,∴ 平面 , 2分
又∵ 平面 ,∴平面 平面 ; 4分(2)取 的中点 ,连接 、 ,易得 是等边三角形,
∴ ,又∵ 平面 ,∴ , 5
分
又 ,∴ 平面 ,
在平面 中,过 作 于 ,则 , 7
分
又 ,∴ 平面 ,
则 是点 在平面 内的正投影, 9
分
经计算得 ,在 中, , , 10分
, , 11
分
∴ 。 12
分
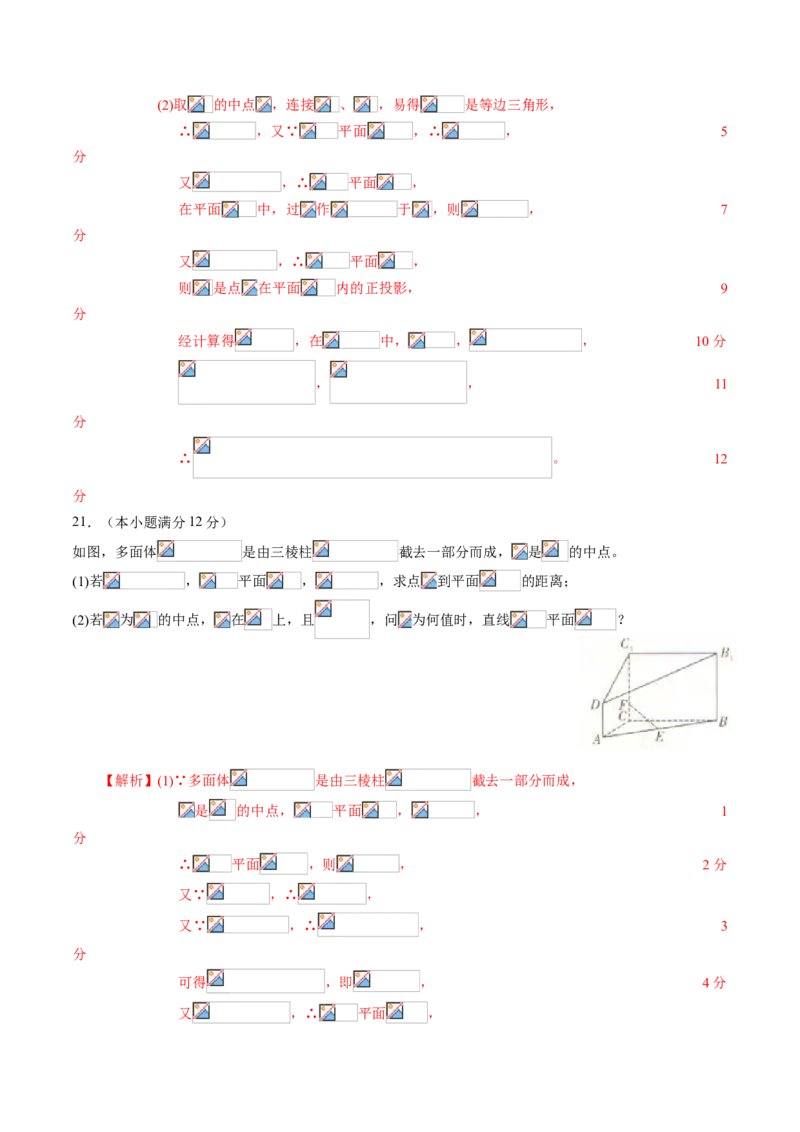
21.(本小题满分12分)
如图,多面体 是由三棱柱 截去一部分而成, 是 的中点。
(1)若 , 平面 , ,求点 到平面 的距离;
(2)若 为 的中点, 在 上,且 ,问 为何值时,直线 平面 ?
【解析】(1)∵多面体 是由三棱柱 截去一部分而成,
是 的中点, 平面 , , 1
分
∴ 平面 ,则 , 2分
又∵ ,∴ ,
又∵ ,∴ , 3
分
可得 ,即 , 4分
又 ,∴ 平面 ,∴点 到平面 的距离 ; 5
分
(2)当 时,直线 平面 ,证明如下:
设 ,则 ,取 的中点 ,连接 ,可得 , 6
分
∵ 是梯形 的中位线,∴ , 8
分
∴当 时,四边形 为平行四边形,即 , 10
分
∵ 平面 ,∴直线 平面 ,此时 。 12分
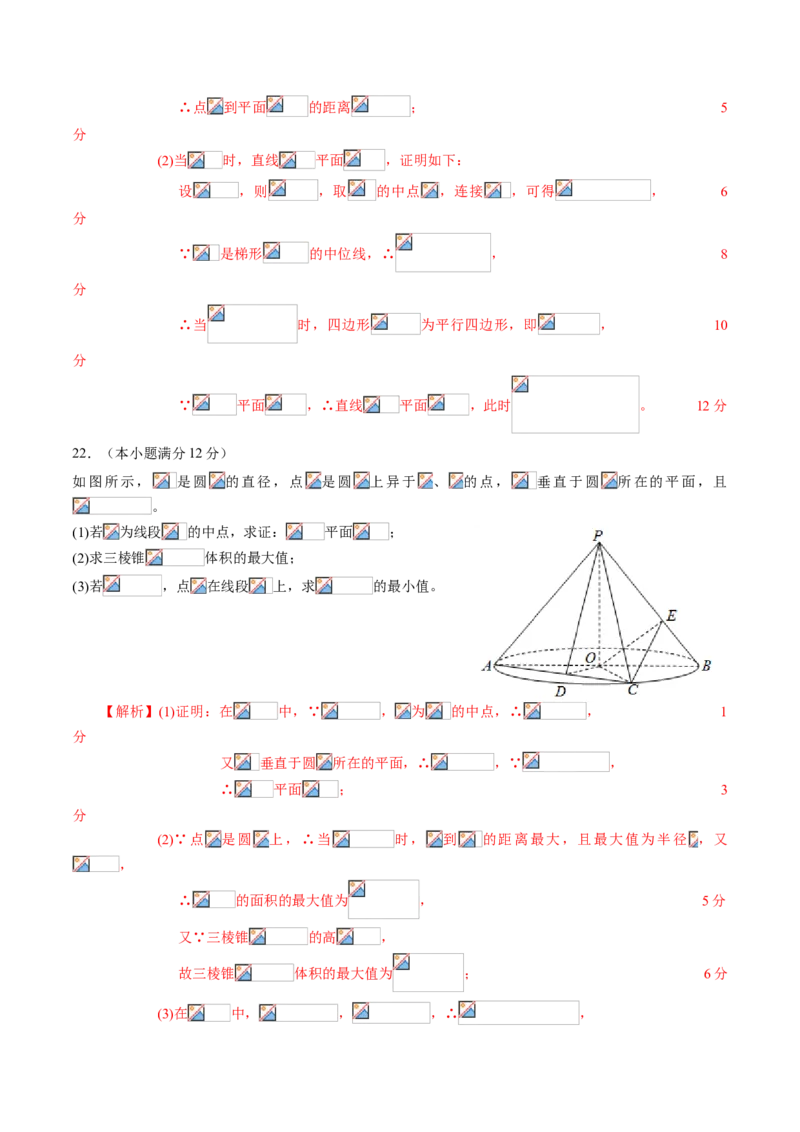
22.(本小题满分12分)
如图所示, 是圆 的直径,点 是圆 上异于 、 的点, 垂直于圆 所在的平面,且
。
(1)若 为线段 的中点,求证: 平面 ;
(2)求三棱锥 体积的最大值;
(3)若 ,点 在线段 上,求 的最小值。
【解析】(1)证明:在 中,∵ , 为 的中点,∴ , 1
分
又 垂直于圆 所在的平面,∴ ,∵ ,
∴ 平面 ; 3
分
(2)∵点 是圆 上,∴当 时, 到 的距离最大,且最大值为半径 ,又
,
∴ 的面积的最大值为 , 5分
又∵三棱锥 的高 ,
故三棱锥 体积的最大值为 ; 6分
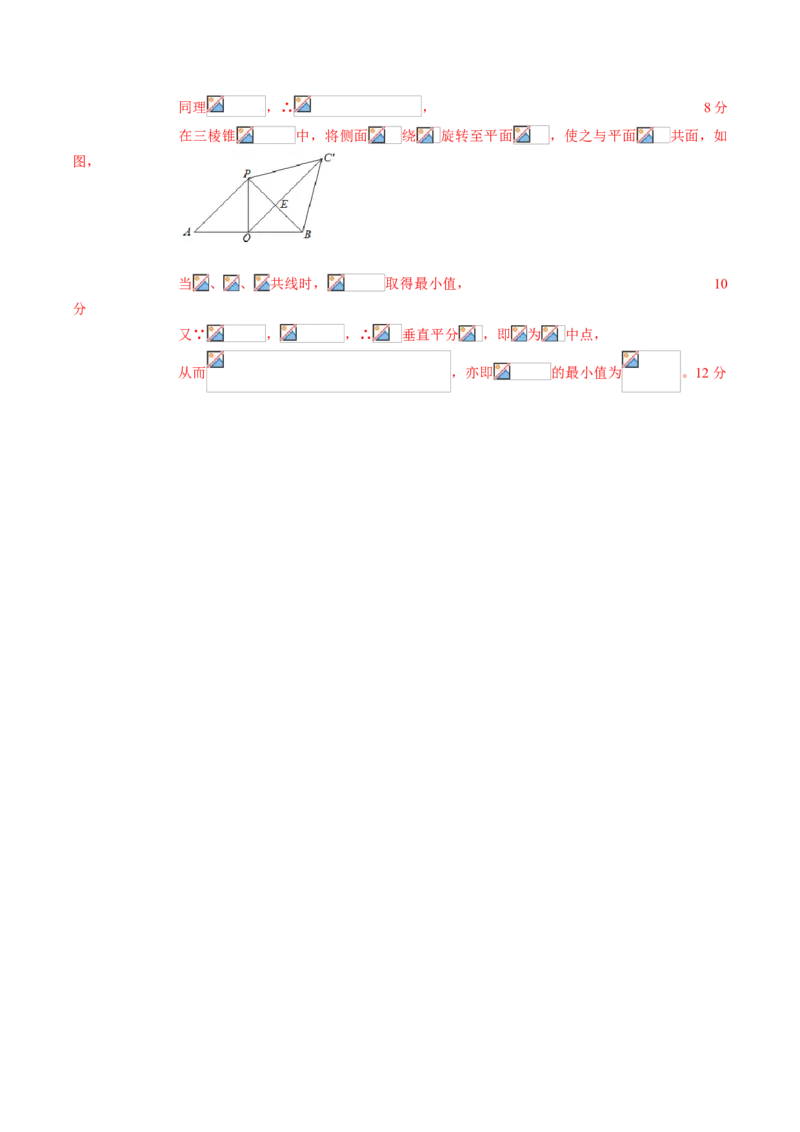
(3)在 中, , ,∴ ,同理 ,∴ , 8分
在三棱锥 中,将侧面 绕 旋转至平面 ,使之与平面 共面,如
图,
当 、 、 共线时, 取得最小值, 10
分
又∵ , ,∴ 垂直平分 ,即 为 中点,
从而 ,亦即 的最小值为 。12分