文档内容
期末模拟卷 2
一、单选题(本大题共8小题,共40.0分)
复数 为虚数单位 在复平面内对应的点位于
1.
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
【解析】
【分析】
本题考查复数的几何意义,直接由复数 求出在复平面内对应的点的坐标得
答案.
【解答】
解:复数 为虚数单位 在复平面内对应的点的坐标为: ,位于第四
象限.
故选D.
2. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
【答案】D
【解析】
【分析】
本题主要考查概率的求法,解题时要认真审题,注意列举法的合理运用,属于基础题.
先求出基本事件总数 ,再用列举法求出抽得的第一张卡片上的数大于第二张卡
片上的数包含的基本事件个数,由此能求出抽得的第一张卡片上的数大于第二张卡片
上的数的概率.
【解答】解:从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数 ,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有: , ,
, , , , , , , ,共有 个基本
事件,
抽得的第一张卡片上的数大于第二张卡片上的数的概率 ,
故选:D.
3. 已知一个三棱柱的高为3,如图是其底面用斜二测画
法画出的水平放置的直观图,其中
,则此三棱柱的体积为
A. 2
B. 4
C. 6
D. 12
【答案】C
【解析】
【分析】
本题考察直观图与原图的关系,以及棱柱的体积公式,属于基础题.
依据直观图可知原图的底面三角形的底边长为2,高为2,可求出柱体的底面面积,再
依据棱柱体积公式可求出答案.
【解答】解:设三棱柱的底面三角形为 ,由直观图可知 , ,
且 , ,
故 .
故答案选C.
4. 已知非零向量 , ,若 ,且 ,则 与 的夹角
为
A. B. C. D.
【答案】B
【解析】
【分析】
本题考查了向量的数量积,考查了向量垂直的关系,考查了向量夹角的求解 本题的关
键是由垂直求出数量积为0.
由向量垂直可得 ,结合数量积的定义表达式可求出
,又 ,从而可求出夹角的余弦值,进而可求夹角的
大小.
【解答】
解:因为 ,
所以 ,因为 ,
所以 ,
.
故选:B.
5. 设 为平面,a,b为两条不同的直线,则下列叙述正确的是
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】B
【解析】
【分析】
本题考查命题的真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培
养.
利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解.
【解答】
解:若 , ,则a与b相交、平行或异面,故A错误;
若 , ,则由直线与平面垂直的判定定理知 ,故B正确;
若 , ,则 或 ,故C错误;若 , ,则 ,或 ,或b与 相交,故D错误.
故选:B.
6. 已知圆锥的顶点为P,母线PA,PB所成角的余弦值为 ,PA与圆锥底面所成角
为 ,若 的面积为 ,则该圆锥的体积为
A. B. C. D.
【答案】C
【解析】
【分析】
本题考查线面角的概念、三角形面积公式、圆锥的体积公式,考查转化与化归思想,
考查空间想象能力、运算求解能力.
设底面半径为 ,根据线面角的大小可得母线长为2r,再根据三角形的面积得
到r的值,最后代入圆锥的体积公式,即可得答案.
【解答】
解:如图所示,设底面半径为 ,与圆锥底面所成角为 , ,
, 母线PA,PB所成角的余弦值为 ,
, ,
,
故选:C.
7. 已知数据 的方差为4,若 ,则
新数据 的方差为
A. 16 B. 13 C. D.
【答案】A
【解析】
【分析】
本题考查利用方差的性质求解方差的问题,属于基础题.
根据方差的性质直接计算可得结果.
【解答】
解:由方差的性质知:新数据 的方差为: .
故选:A.8. 在 中,A,B,C所对的边分别是a,b,c,若 ,且
,则
A. 3 B. 4 C. 5 D. 6
【答案】D
【解析】
【分析】
本题主要考查正弦定理和余弦定理的应用,属于中档题.
根据题目已知条件应用余弦定理和正弦定理进行化简,即可得到答案.
【解答】
解: ,
,
,
,又 .
代入可得
故答案选D.
二、多选题(本大题共4小题,共20.0分)
9. 有甲 乙两种报纸供市民订阅,记事件E为“只订甲报纸”,事件F为“至少订
一种报纸”,事件G为“至多订一种报纸”,事件H为“不订甲报纸”,事件I
为“一种报纸也不订” 下列命题正确的是
A. E与G是互斥事件 B. F与I是互斥事件,且是对立事件
C. F与G不是互斥事件 D. G与I是互斥事件
【答案】BC
【解析】
【分析】
本题考查了互斥事件和对立事件的概念,属于基础题.根据互斥事件、对立事件的概念判断即可.
【解答】
解:对于A选项,E、G事件有可能同时发生,不是互斥事件;
对于B选项,F与I不可能同时发生,且发生的概率之和为1,是互斥事件,且是对立
事件;
对于C选项,F与G可以同时发生,不是互斥事件;
对于D选项,G与I也可以同时发生,不是互斥事件.
故选:BC.
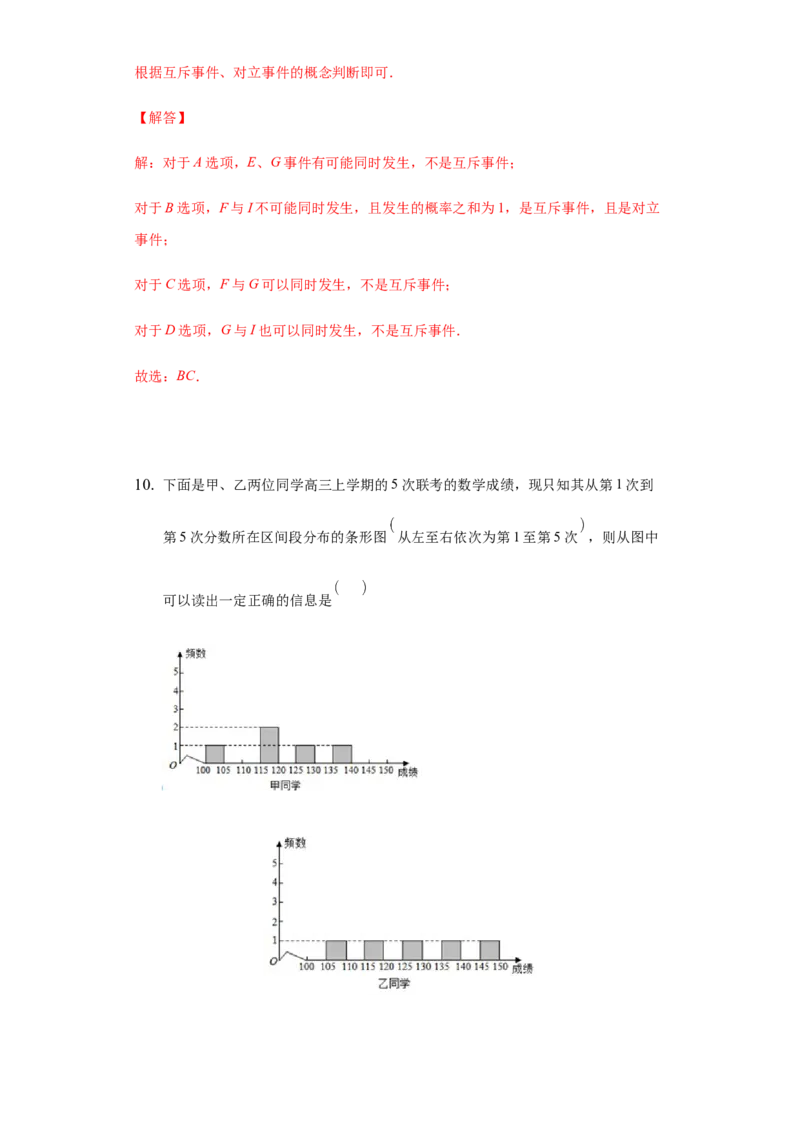
10. 下面是甲、乙两位同学高三上学期的5次联考的数学成绩,现只知其从第1次到
第5次分数所在区间段分布的条形图 从左至右依次为第1至第5次 ,则从图中
可以读出一定正确的信息是A. 甲同学的成绩的平均数大于乙同学的成绩的平均数
B. 甲同学的成绩的中位数在115到120之间
C. 甲同学的成绩的极差小于乙同学的成绩的极差
D. 甲同学的成绩的中位数小于乙同学的成绩的中位数
【答案】DB
【解析】
【分析】
本题考查了频数分布直方图与应用问题,是基础题.
根据频数分布直方图的数据,对选项中的命题进行分析,判断正误即可.
【解答】
解:对于A,甲同学的成绩的平均数 ,
乙同学的成绩的平均数 ,
所以甲同学的成绩的平均数小于乙同学的成绩的平均数,故A错误;
由题图甲知,B正确;
对于C,由题图知,甲同学的成绩的极差介于 之间,乙同学的成绩的极差介于
之间,
所以甲同学的成绩的极差也可能大于乙同学的成绩的极差,故C错误;
对于D,甲同学的成绩的中位数在 之间,乙同学的成绩的中位数在
之间,
所以甲同学的成绩的中位数小于乙同学的成绩的中位数,故D正确.
故选:BD.11. 下列结论正确的是
A. 已知 是非零向量, ,若 ,则
B. 向量 , 满足 , , 与 的夹角为 ,则 在 上的投影向
量为
C. 点P在 所在的平面内,满足 ,则点P是
的外心
D. 以 , , , 为顶点的四边形是一个矩形
【答案】DBA
【解析】
【分析】
本题考查向量数量积的运算,向量的坐标运算,向量垂直的转化,属中档题.
利用平面向量的数量积运算,结合向量的线性运算,对每个选项进行逐一分析,即可
容易判断选择.
【解答】
解:对A:因为 ,
又 ,可得 ,
故 ,故A选项正确;对B:因为 , , 与 的夹角为 ,
所以 .
故 在 上的投影向量为 ,故B选项正确;
对C:点P在 所在的平面内,满足 ,
则点P为三角形ABC的重心,故C选项错误;
对D:不妨设 ,
则 ,
故四边形ABCD是平行四边形;
又 ,
所以 ,故四边形ABCD是矩形 故D选项正确;
综上所述,正确的有ABD.
故选ABD.12. 如图,在四棱锥 中,底面ABCD是正方
形, 底面ABCD, ,截面BDE与直
线PC平行,与PA交于点E,则下列判断正确的是
A. E为PA的中点
B. 平面PAC
C. PB与CD所成的角为
D. 三棱锥 与四棱锥 的体积之比等于 .
【答案】ABD
【解析】
【分析】
本题考查立体几何的综合应用,熟练线线、线面、面面之间的位置关系,审清题意,
考验分析能力,属中档题.
采用排除法,根据线面平行的性质定理以及线面垂直的判定定理,结合线线角的求法,
锥体体积公式的计算,可得结果.
【解答】
解:对于A,连接AC交BD于点M,连接EM,如图所示,
面BDE, 面APC,且面 面 , ,又 四边形ABCD是正方形, 为AC的中点,
为PA的中点,故A正确.
对于B, 面ABCD, 面ABCD, ,
又 , , 面PAC
面PAC,故B正确.
对于C, , 为PB与CD所成的角,
面ABCD, 面ABCD, ,
在 中, , ,故C错误.
对于D,由等体积法可得 ,
又 , ,故D正确.
故选:ABD.
三、填空题(本大题共4小题,共20.0分)
13. 若复数z满足方程 ,则 .【答案】
【解析】
【分析】
本题考查复数的计算,属基础题.
根据题意可得 ,然后根据复数的乘法可得结果.
【解答】
解:由 ,则 ,
所以 ,
所以 ,
故答案为:
14. 如图,在平行四边形ABCD中,M,N分别为AD,AB上的点,且
,MN交于点 若 ,则 的值为 .
【答案】
【解析】
【分析】本题考查平面向量共线定理的推论,涉及向量的线性运算,属基础题.
用向量 表示 ,结合 三点共线,即可求得参数值.
【解答】
解:根据题意,
,
因为 三点共线,
所以 ,解得 .
故答案为 .
15. 某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出
两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是
,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一
轮的概率等于 .
【答案】
【解析】
【分析】
本题考查相互独立事件的概率乘法公式,属于基础题.
根据题意,若该选手恰好回答了4个问题就晋级下一轮,必有第二个问题回答错误,
第三、四个问题回答正确,第一个问题可对可错.
【解答】解:根据题意,记“该选手恰好回答了4个问题就晋级下一轮”为事件A,
若该选手恰好回答了4个问题就晋级下一轮,
必有第二个问题回答错误,第三、四个问题回答正确,第一个问题可对可错;
由相互独立事件的概率乘法公式,
可得 ,
故答案为 .
16. 如图,在正方体 中,点O为线段
BD的中点,设点P在线段 上,直线OP与平面
所成的角为 ,则 的最小值 ,最大
值 .
【答案】
1
【解析】
【分析】
此题考查正方体的性质和直角三角形的边角关系,线面角的求法,考查推理能力,属
于中档题。
由题意,直线OP与平面 所成的角 的最小值为 和 中的最小者,
然后利用正方体的性质和直角三角形的边角关系,求出 的取值范围,再确定其最
值
【解答】解:连接 , ,
因为 , 平面 ,
所以 平面 ,
又 平面
所以平面 平面 ,
所以直线OP与平面 所成的角 的最小值为 和 中的最小者,
不妨设 ,
在 中, ,,
所以 的取值范围为 ,
所以 的最小值为 ,最大值为1,
故答案为: ;1.
四、解答题(本大题共6小题,共70.0分)
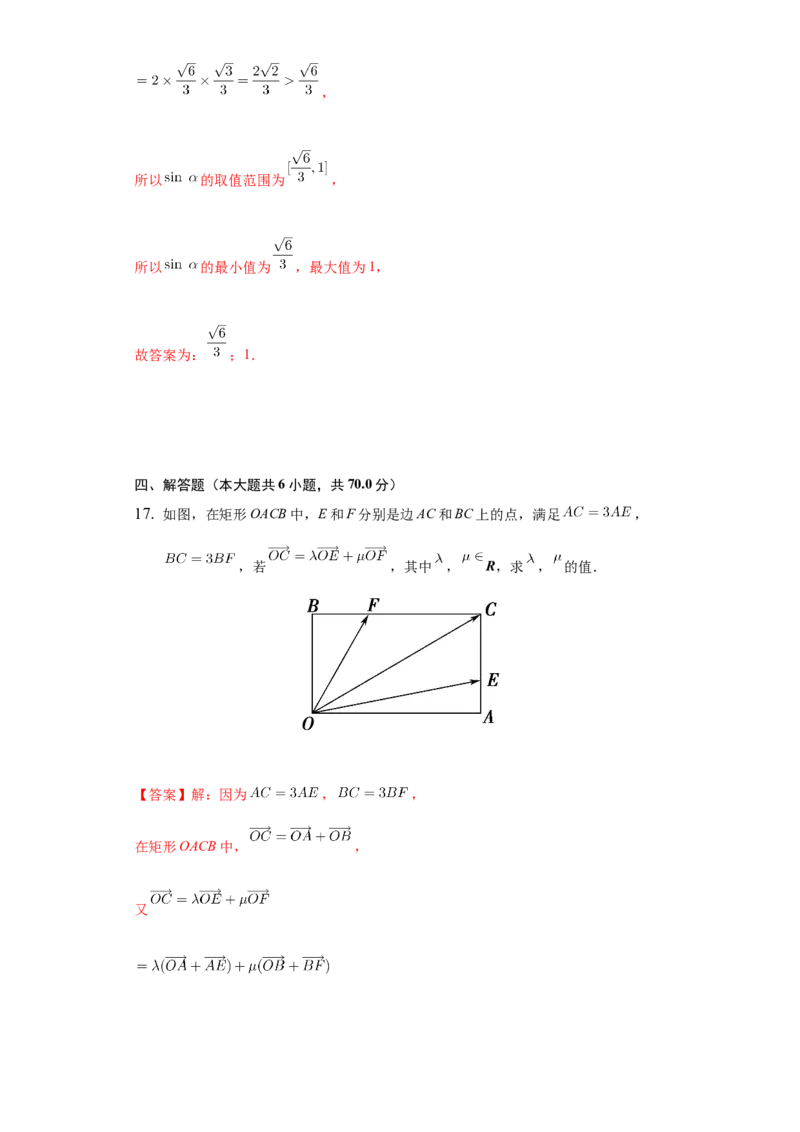
17. 如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足 ,
,若 ,其中 , R,求 , 的值.
【答案】解:因为 , ,
在矩形OACB中, ,
又,
所以 , ,
所以 .
【解析】本题考查平面向量基本定理,属于基础题.
根据题意得出 ,则 ,
由此即可求出结果.
18. 已知函数 ,且当 时, 的最小
值为2.
求a的值,并求 的单调递增区间;
先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的 ,再将所
得的图象向右平移 个单位,得到函数 的图象,当 时,求
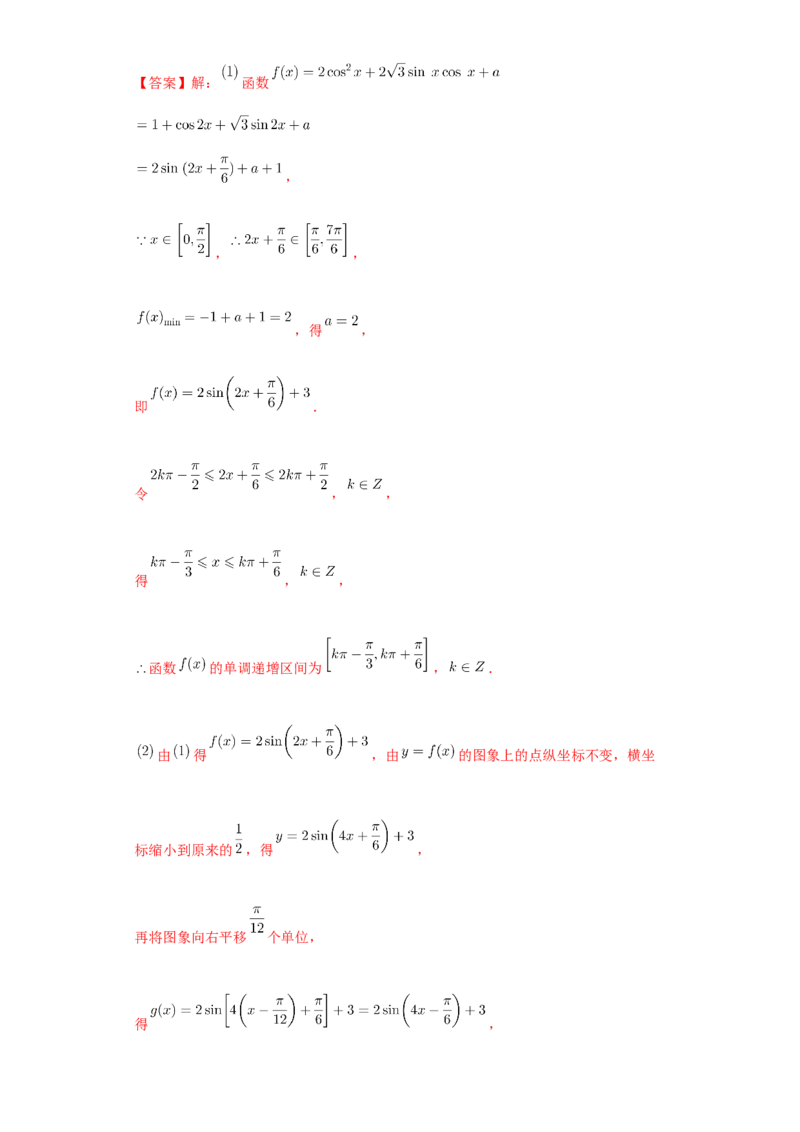
的x的集合.【答案】解: 函数
,
, ,
,得 ,
即 .
令 , ,
得 , ,
函数 的单调递增区间为 , .
由 得 ,由 的图象上的点纵坐标不变,横坐
标缩小到原来的 ,得 ,
再将图象向右平移 个单位,
得 ,又 ,即 ,
,
即 ,
,
不等式的解集 .
【解析】本题主要考查了二倍角和辅助角公式,求三角函数的单调区间,三角函数图
象变换,解三角不等式等,属于中档题.
化简可得 ,由题意可得, ,解方程
可得a的值,解不等式 , 可得单调递增区间.
由函数图象变换可得: ,可得 ,令
,解不等式与 求交集即可.19. 如图,在棱长均为1的直三棱柱 中,D
是BC的中点.
求证: 平面
求直线 与平面 所成角的正弦值.
【答案】 证明:直三棱柱 中, 平面ABC, 平面
ABC,
,
,D是BC的中点,
,
又 ,BC、 平面 ,
平面 .
解:如图,连接 ,
由 可知, 平面 ,
则 即为直线 与平面 所成角,因为 平面 , 平面 ,
所以 ,
在 中, , ,
所以 ,
所以直线 与平面 所成角的正弦值为 .
【解析】本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到 ,并且 ,从而由线面垂直的判定定理可得到
平面 ;
连接 ,可得到 为直线 和平面 所成角,即可得解.
本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到 ,并且 ,从而由线面垂直的判定定理可得到
平面 ;
连接 ,可得到 为直线 和平面 所成角,即可得解.
20. 某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随
机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间 满分
150分 ,将统计结果按如下方式分成八组:第一组 ,第二组 ,
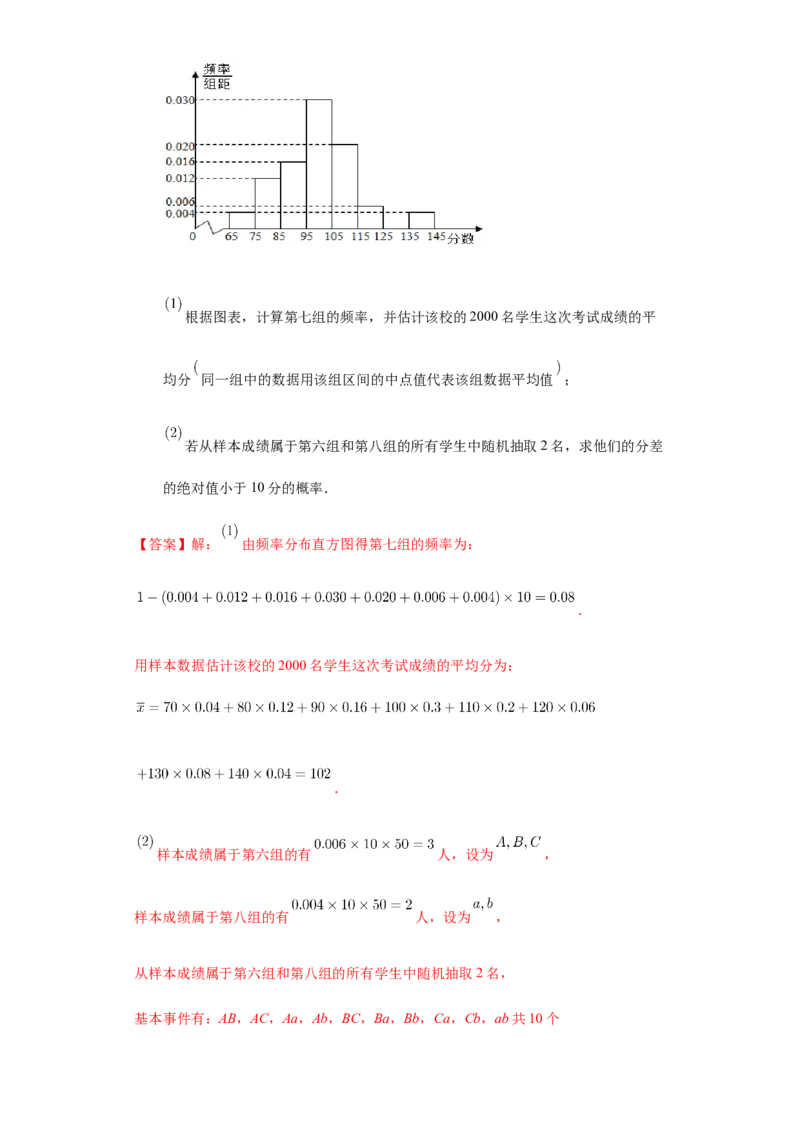
第八组 ,如图是按上述分组方法得到的频率分布直方图的一部分.根据图表,计算第七组的频率,并估计该校的2000名学生这次考试成绩的平
均分 同一组中的数据用该组区间的中点值代表该组数据平均值 ;
若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差
的绝对值小于10分的概率.
【答案】解: 由频率分布直方图得第七组的频率为:
.
用样本数据估计该校的2000名学生这次考试成绩的平均分为:
.
样本成绩属于第六组的有 人,设为 ,
样本成绩属于第八组的有 人,设为 ,
从样本成绩属于第六组和第八组的所有学生中随机抽取2名,
基本事件有:AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab共10个他们的分差的绝对值小于10分,即在同一组中包含的基本事件有:AB,AC,BC,ab
共4个
他们的分差的绝对值小于10分的概率 .
【解析】本题考查利用频率分布直方图求解样本数据的平均值,考查古典概型概率的
计算,难度中档.
计算样本数据的平均值时,只需利用每组中间值乘以本组频率求和即可得到答案;
古典概型的解答注意分析清楚基本事件总数及某事件成立时所包含的基本事件数.
利用所有组频率和为1即可求得第七组的频率,然后利用 其中 表示
第i组的中间值, 表示该组的频率 求出平均值;
利用古典模型概率的计算方法求解即可.
21. 在 中,内角A,B,C的对边分别为a,b,c,若 .
求A的大小;
若 , ,求 的面积.
【答案】解: ,由正弦定理得:
,
, , ,又 , ;由余弦定理可得 ,
, , , ,或 舍去
.
【解析】本题考查三角形的解法,正弦定理以及余弦定理的应用,考查计算能力.
由 与正弦定理可得 ,又 ,得 ;
由 , 与余弦定理可得 ,得 ,由
可得结果.
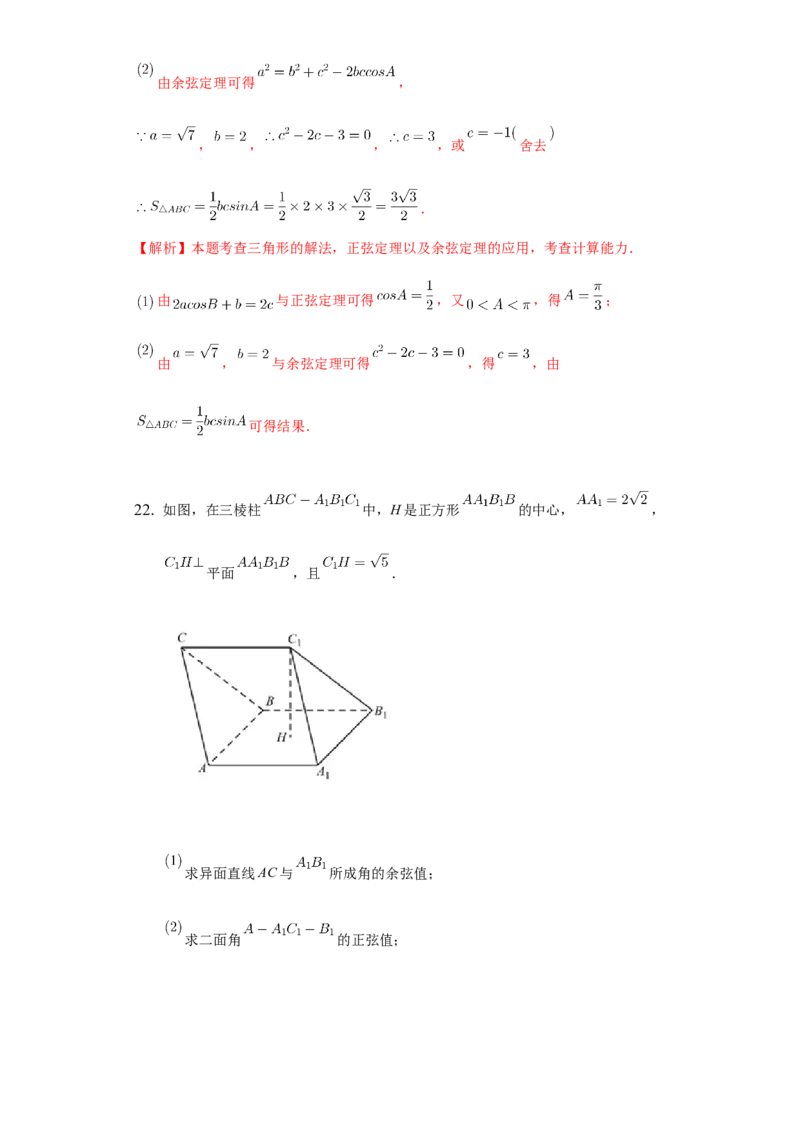
22. 如图,在三棱柱 中,H是正方形 的中心, ,
平面 ,且 .
求异面直线AC与 所成角的余弦值;
求二面角 的正弦值;设N为棱 的中点,E在 上,并且 ,点M在平面
内,且 平面 ,证明: 平面 .
【答案】解: 连接 , 为正方形 的中心, ,则
, ,
在三棱柱 中, ,
或补角 是异面直线AC与 所成的角.
平面 , 平面 , ,
,可得 ,
由余弦定理得 ,
因此,异面直线AC与 所成角的余弦值为 ;
连接 , 平面 , 平面 , ,
为 的中点,则 ,又由于 , , ,
,
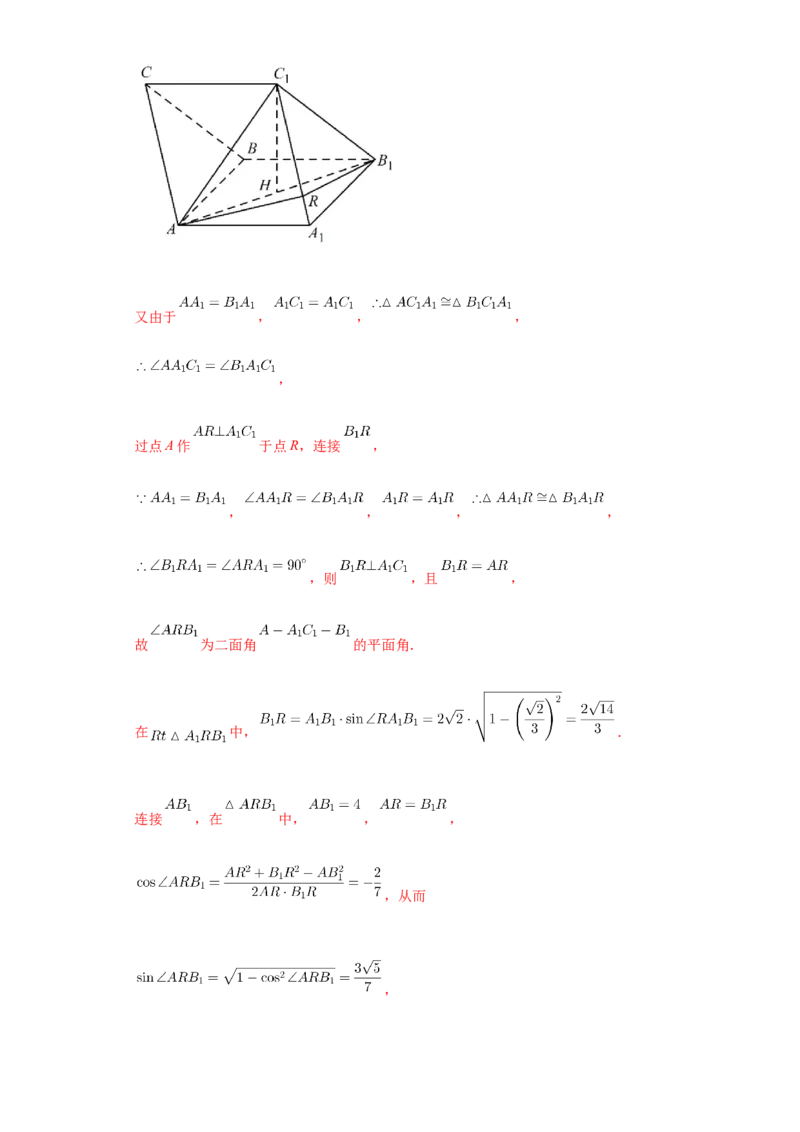
过点A作 于点R,连接 ,
, , , ,
,则 ,且 ,
故 为二面角 的平面角.
在 中, .
连接 ,在 中, , ,
,从而
,因此,二面角 的正弦值为 .
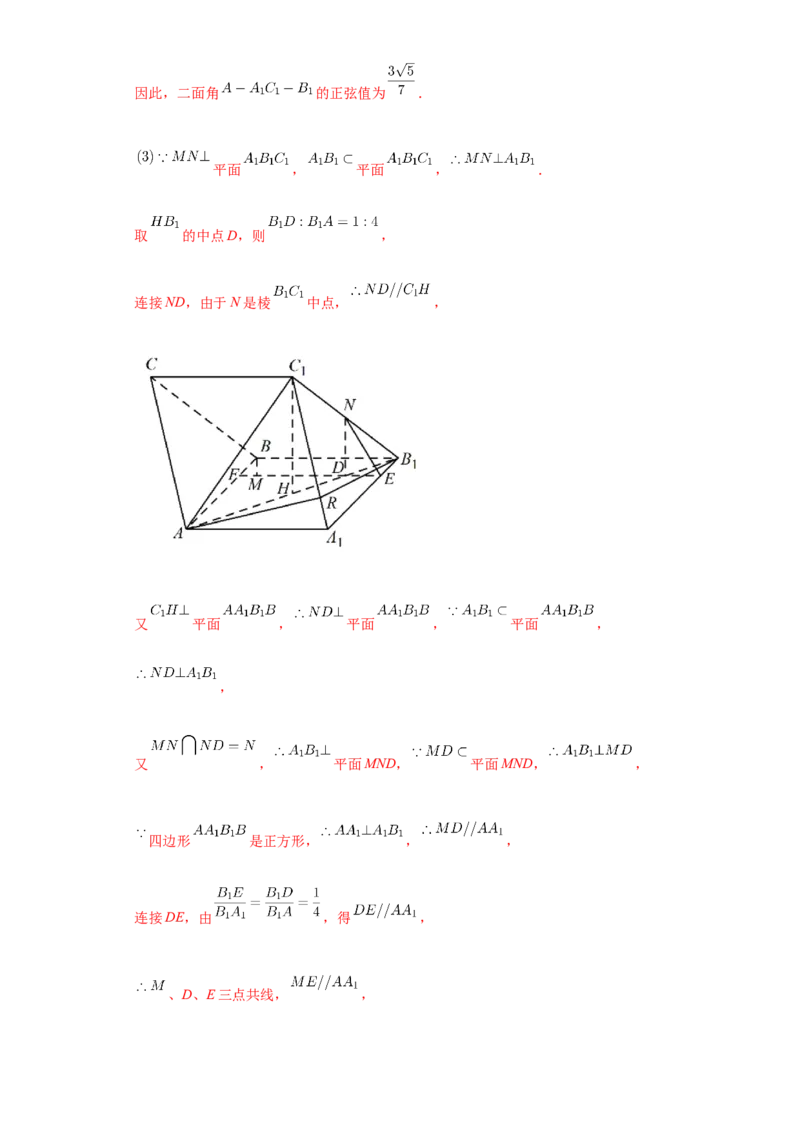
平面 , 平面 , .
取 的中点D,则 ,
连接ND,由于N是棱 中点, ,
又 平面 , 平面 , 平面 ,
,
又 , 平面MND, 平面MND, ,
四边形 是正方形, , ,
连接DE,由 ,得 ,
、D、E三点共线, ,平面 , 平面 , 平面 .
【解析】本题考查异面直线所成角、二面角的计算,同时也考查了线面平行的证明,
考查推理能力与计算能力,属于中等题.
连接 ,由 可知 或补角 是异面直线AC与 所成的角,
计算出 各边边长,利用余弦定理可求得 的值,进而得解;
连接 ,过点A作 于点R,连接 ,证明 ,可得出
为二面角 的平面角,计算出 的三边边长,利用余弦定
理可求得 ,利用同角三角函数的基本关系可求得二面角 的
正弦值;
取 的中点D,连接ND,证明出 平面MND,可得出 ,进而
推导出 ,推导出 ,可得出M、D、E三点共线,进而得出
,利用线面平行的判定定理可得出 平面 .