文档内容
期末测试卷 01
满分:150分 时间:120分钟
一、单项选择题(4分×10题=40分)
a+i
1.已知a是实数, 是纯虚数,则a等于( )
1-i
A.-❑√2 B.-1 C. ❑√2 D. 1
2.已知向量a=(2,1),b=(x,-2),若a// b,则a+b=( )
A.(-2,-1) B.(2,1) C.(3,-1) D.(-3,1)
3.正四面体ABCD中,E、F分别是AB、CD的中点,则异面直线EF与BC所成的角
等于( )
A.30° B.45° C.60° D.120°
4.在△ABC中,若A=30°,a=8,b=8❑√3,则S =( )
△ABC
A.32❑√3 B.16❑√3 C.32❑√3或16❑√3 D.12❑√3
1
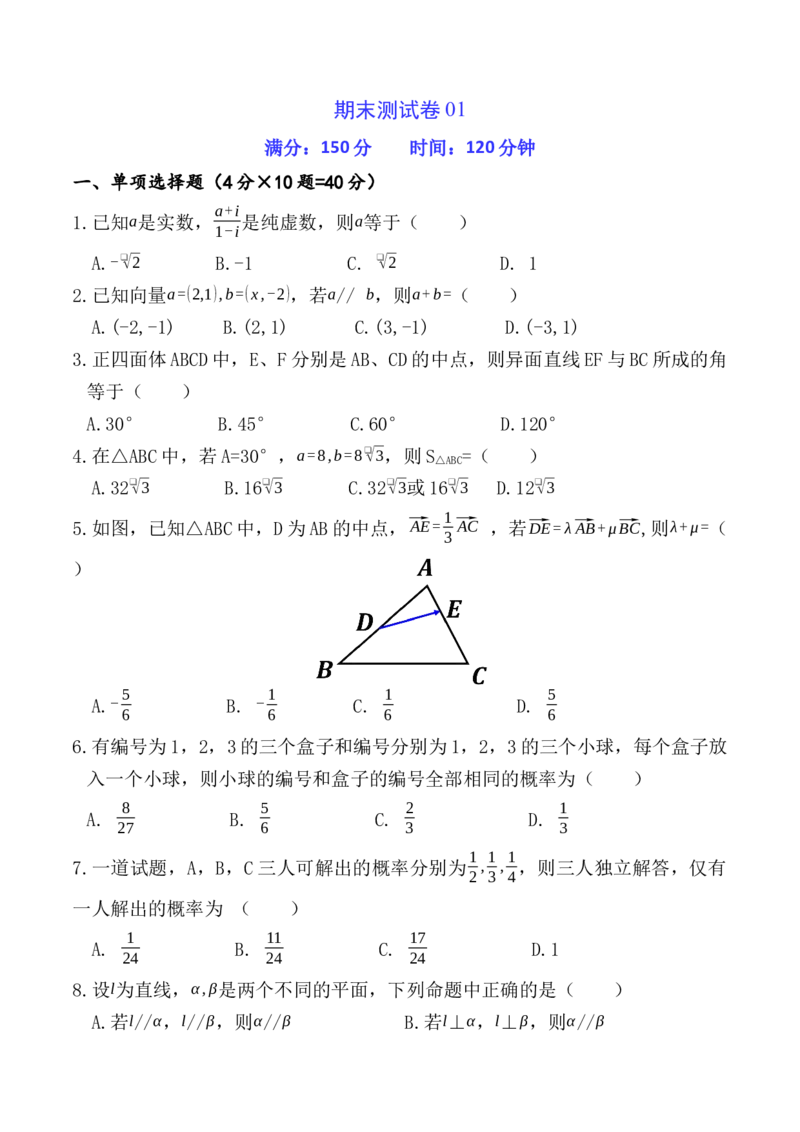
5.如图,已知△ABC中,D为AB的中点,⃗AE= ⃗AC ,若⃗DE=λ⃗AB+μ⃗BC,则λ+μ=(
3
)
5 1 1 5
A.- B. - C. D.
6 6 6 6
6.有编号为1,2,3的三个盒子和编号分别为1,2,3的三个小球,每个盒子放
入一个小球,则小球的编号和盒子的编号全部相同的概率为( )
8 5 2 1
A. B. C. D.
27 6 3 3
1 1 1
7.一道试题,A,B,C三人可解出的概率分别为 , , ,则三人独立解答,仅有
2 3 4
一人解出的概率为 ( )
1 11 17
A. B. C. D.1
24 24 24
8.设l为直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若l//α,l//β,则α//β B.若l⊥α,l⊥β,则α//βC. 若l⊥α,l//β,则α//β D.若α⊥β,l//α,则l⊥β
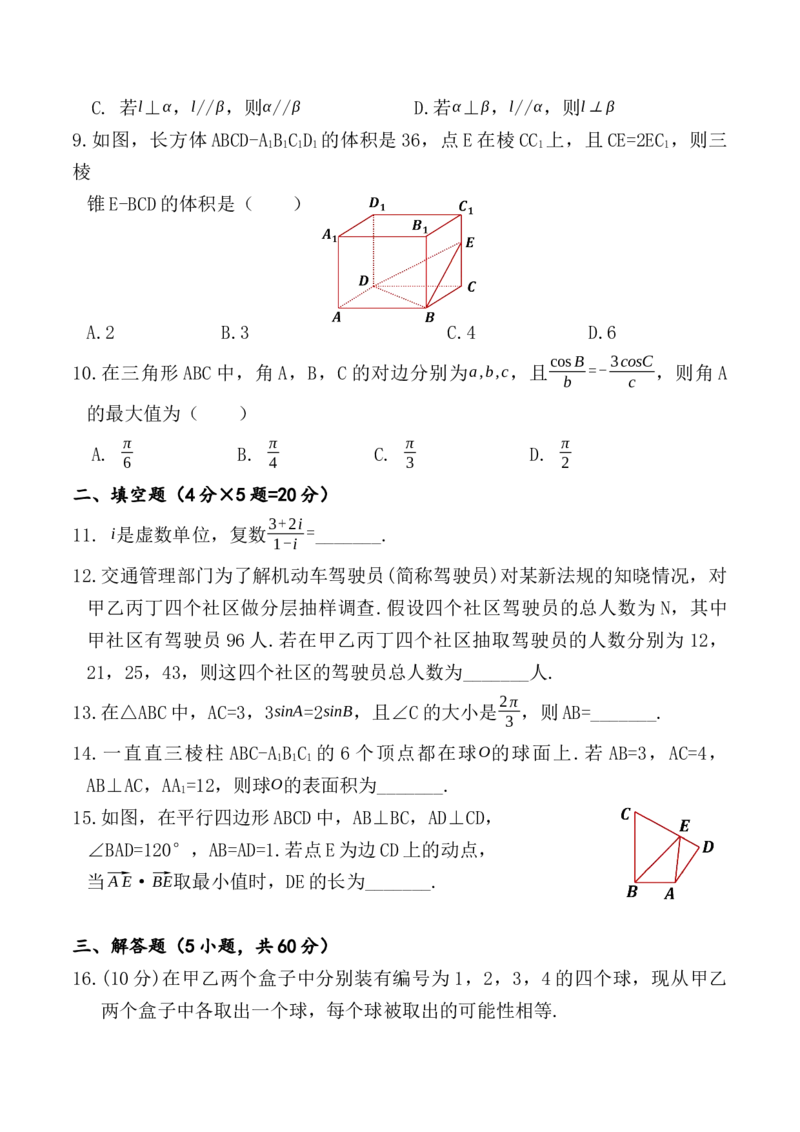
9.如图,长方体 ABCD-A B C D 的体积是 36,点 E 在棱 CC 上,且 CE=2EC ,则三
1 1 1 1 1 1
棱
锥E-BCD的体积是( )
A.2 B.3 C.4 D.6
cosB 3cosC
10.在三角形 ABC 中,角 A,B,C 的对边分别为a,b,c,且 =- ,则角 A
b c
的最大值为( )
π π π π
A. B. C. D.
6 4 3 2
二、填空题(4分×5题=20分)
3+2i
11. i是虚数单位,复数 =_______.
1-i
12.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对
甲乙丙丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为 N,其中
甲社区有驾驶员 96 人.若在甲乙丙丁四个社区抽取驾驶员的人数分别为 12,
21,25,43,则这四个社区的驾驶员总人数为_______人.
2π
13.在△ABC中,AC=3,3sinA=2sinB,且∠C的大小是 ,则AB=_______.
3
14.一直直三棱柱 ABC-A B C 的 6 个顶点都在球O的球面上.若 AB=3,AC=4,
1 1 1
AB⊥AC,AA =12,则球O的表面积为_______.
1
15.如图,在平行四边形ABCD中,AB⊥BC,AD⊥CD,
∠BAD=120°,AB=AD=1.若点E为边CD上的动点,
当⃗AE·⃗BE取最小值时,DE的长为_______.
三、解答题(5小题,共60分)
16.(10 分)在甲乙两个盒子中分别装有编号为 1,2,3,4 的四个球,现从甲乙
两个盒子中各取出一个球,每个球被取出的可能性相等.(1)请列出所有可能的结果
(2)求取出的两个球的编号恰为相邻整数的概率
(3)求取出的两个球的编号之和与编号之积都不小于4的概率
17.(12 分 ) 在 △ ABC 中 , 内 角 A , B , C 所 对 的 边 分 别 为 a,b,c. 已 知
asinA=4bsinB,ac=❑√5(a2-b2-c2 ).
(1)求cosA的值
(2)求sin(2B-A)的值
18.(12分)已知|a|=4,|b|=3,(2a-3b)·(2a-b)=43.
(1)求a与b的夹角θ
(2)求|a+b|
(3)若(a-b)⊥(a+λb),求实数λ的值
19.(13 分)在如图所示的四棱锥 P-ABCD 中,已知 PA⊥平面 ABCD,AD//BC,
∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
(1)求证:CE//平面PAD
(2)求证:平面PAC⊥平面PDC
(3)求直线EC与平面PAC所成角的正切值20.(13分)如图,四棱柱ABCD-A B C D 的底面ABCD是菱形,AA ⊥平面ABCD,
1 1 1 1 1
AB=1,AA =2,∠BAD=60°,点P为DD 中点.
1 1
(1)求证:直线BD //平面PAC
1
(2)求证:BD ⊥AC
1
(3)求二面角B -AC-P的余弦值.
1