数学答案——2024年7月高一期末调研考试_2024-2025高一（7-7月题库）_2024年7月试卷_0704河北省保定市2023-2024学年高一下学期期末调研考试

2023-2024 学年第二学期高一数学期末调研考试 参考答案 一、选择题：本题共8 小题，每小题 5 分，共40 分。 1.A. 2. D 3.C 4．B 5.D 6.B 7.C 8.C 二、选择题：本题共 3 小题，每小题6 分，共 18分。在每小题给出的选项中，有多项符合题 目要求。全部选对的得 6分，部分选对的得部分分，有选错的得 0 分。（部分选对中如有 三个正确选项，选对一个得 2 分，选对两个得 4 分；如有两个正确选项，选对一个得 3 分.） 9.ACD 10.BD 11.ABD 三、填空题：本题共 3小题，每小题 5分，共 15 分。 1 12.  13．225 14.208 2 四、解答题：本题共 5小题，共 77 分。解答应写出文字说明、证明过程或演算步骤。 2 15.解： （1）（0.002+0.003+0.006+a+0.018+0.008+0.004）×20=1 …………………1分 即0.041+a=0.05 a=0.009 ……………………………………………………………2分 由图可知，学习时长在170分钟以下的团员所占比例为： （0.002+0.003+0.006+0.009）×20=0.4=40% ……………………………………3分 学习时长在190分钟以下的团员所占的比例为：0.4+0.018×20=0.76=76% ……4分  170，190  因此，67%分位数一定位于 内， 0.670.40 法1：由170 20185 0.760.40 法2：设样本数据的67%分位数约为x,则（x-170）×0.018=0.67-0.40，解得x=185 可以估计学习时长的样本数据的67%分位数约为185. ……………………………8分 （2）由图可知，学习时长位于  150，170  内的团员共有10000.00920180人 ，…10分 因为采用的是比例分配的分层随机抽样方法，从1000人中再抽取50人参加座谈 50  150，170  1809人 所以参加座谈的团员中学习时长在区间 内有1000 .……………13分 16.解： (1)证明：连接AD , 1 1 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#} ABCDABCD 为长方体， AB平面ADDA …………1分 1 1 1 1 1 1  AD 平面ADD A , AB  AD …………………………………………………2分 1 1 1 又点E在棱AB上移动， AD  AE …………………………………………………3分 1  AD  AA 1，四边形ADD A 为正方形，  AD  AD ………………………4分 1 1 1 1 1 又AD D E  D且AD  面AD E,D E  面AD E 1 1 1 1 1 1 1 AD 面AD E ………………………………………6分 1 1 又AE  面AD E 1 AD  AE 1 ………………………………………………………………………………………………7分 (2)解：  A  E   1 A  B  ,  AE 1,BE 1 ………………………………………………8分 2 连接DE,计算得 DE 2,EC 2 ，DC= 2 ，由勾股定理逆定理得DE CE , ………10分 法1：DD面ABCD且CE面ABCDDDCE， 1 1 又DD面DDE，DE 面DDE，DDDE DCE  面DDE ,CE DE 1 1 1 1 1 1 法2： DD面ABCD且DE面ABCDDD DEDE 3 1 1 1 又EC 2,DC 5 1 EC2 DE2 5 DC2DE EC 1 1 1 DED为二面角D ECD的平面角 …………………………………………13分 1 1 DD  DE 由题可知 1 ,所以在直角三角形DDE中， 1 DE  2 ,DD1, tanDED= 2 …………………………………………………15分 1 1 2 17.解： （1）用数字m表示第一次抛掷骰子出现的点数是m，数字n表示第一次抛掷骰子出现的点数 是n，则数组 表示这个试验的一个样本点。因此该试验的样本空间   m,n =  m,n  m,n 1,2,3,4,5,6  其中共有36个样本点. ………………………2分 记“两次点数之和为6”为事件A, 则A={（1,5），（5,1），（2,4），（4,2），（3,3）}，即n(A)=5 ………………………3分 2 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#}记“两次点数之和能被4整除”为事件B, 则B={（1,3），（3,1），（2,2），（2,6），（6,2），（3,5），（5,3），（4,4），（6,6）}， 即n(B)=9 ………………………4分 连续掷骰子两次的基本事件总数为36. 5 所以由乙先发球的概率为 ， ………………………5分 36 1 由丙先发球的概率为4 ， ………………………6分 这个方法不公平. 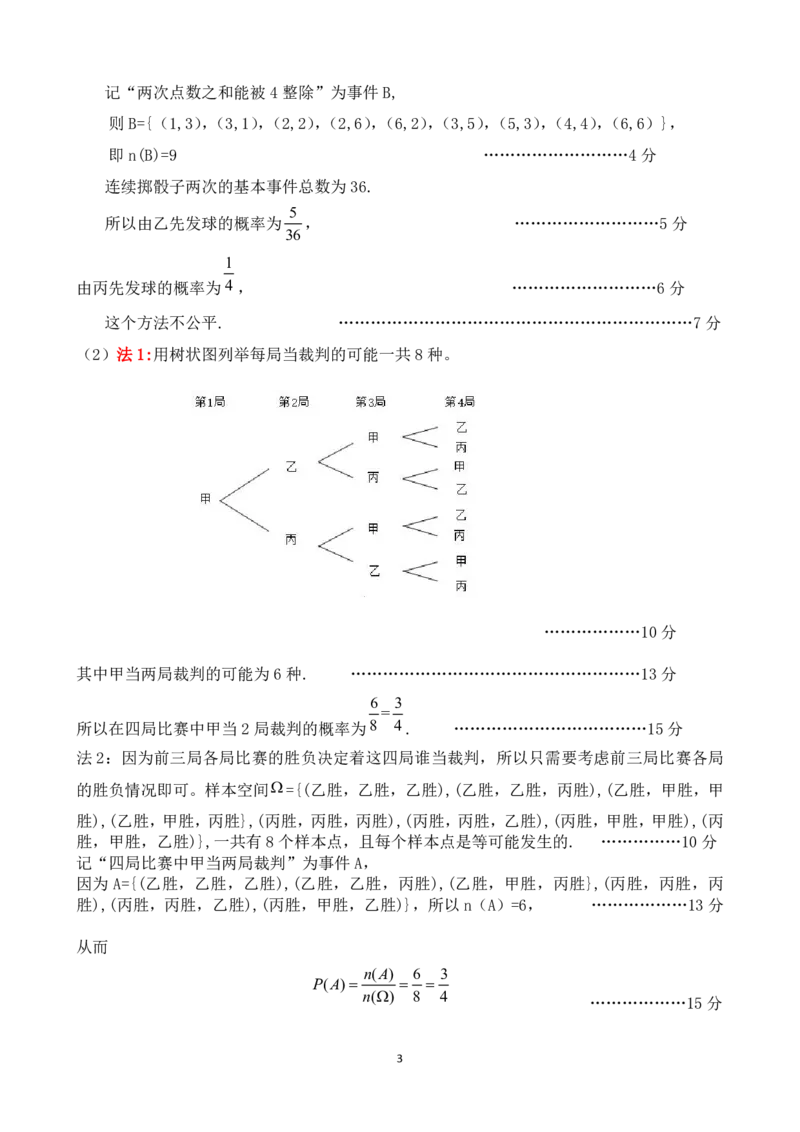…………………………………………………………7分 （2）法1:用树状图列举每局当裁判的可能一共8种。 ………………10分 其中甲当两局裁判的可能为6种. ………………………………………………13分 6 3 = 所以在四局比赛中甲当2局裁判的概率为8 4. ………………………………15分 法 2：因为前三局各局比赛的胜负决定着这四局谁当裁判，所以只需要考虑前三局比赛各局 的胜负情况即可。样本空间={(乙胜，乙胜，乙胜),(乙胜，乙胜，丙胜),(乙胜，甲胜，甲 胜),(乙胜，甲胜，丙胜},(丙胜，丙胜，丙胜),(丙胜，丙胜，乙胜),(丙胜，甲胜，甲胜),(丙 胜，甲胜，乙胜)},一共有8个样本点，且每个样本点是等可能发生的. 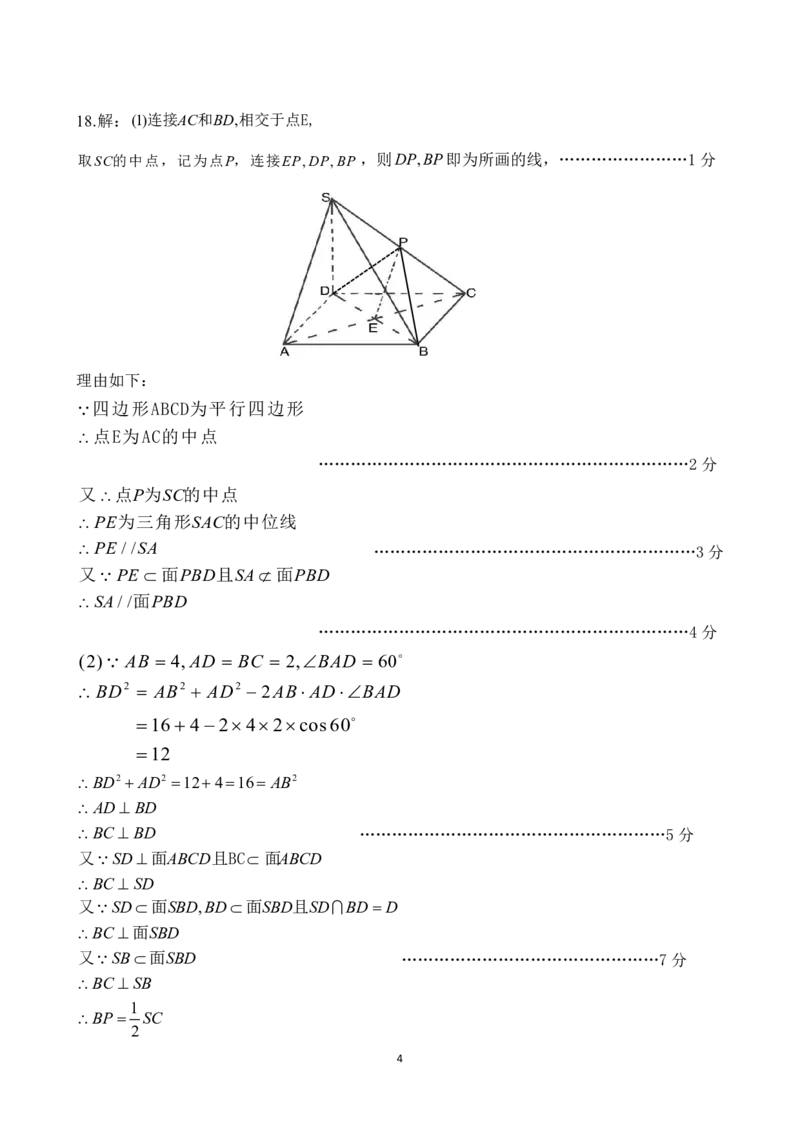……………10分 记“四局比赛中甲当两局裁判”为事件A， 因为 A={(乙胜，乙胜，乙胜),(乙胜，乙胜，丙胜),(乙胜，甲胜，丙胜},(丙胜，丙胜，丙 胜),(丙胜，丙胜，乙胜),(丙胜，甲胜，乙胜)}，所以n（A）=6， ………………13分 从而 n(A) 6 3 P(A)   n() 8 4 ………………15分 3 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#}18.解：(1)连接AC和BD,相交于点E, 取SC的中点，记为点P，连接EP,DP,BP ，则DP,BP即为所画的线，……………………1分 理由如下： 四边形ABCD为平行四边形  点E为AC的中点 ……………………………………………………………2分 又点P为SC的中点 PE为三角形SAC的中位线 PE / /SA ……………………………………………………3分 又 PE  面PBD且SA  面PBD SA/ /面PBD ……………………………………………………………4分 (2) AB  4, AD  BC  2,BAD  60 BD2  AB2  AD2  2AB ADBAD 16 4 242cos60 12 BD2 AD2 12 416 AB2 AD BD BC  BD …………………………………………………5分 又SD 面ABCD且BC 面ABCD BC  SD 又SD面SBD,BD面SBD且SDBD  D BC 面SBD 又SB面SBD …………………………………………7分 BC  SB 1 BP  SC 2 4 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#}又SD DC 1 DP SC 2 又SC  SD2DC2  416  2 5 DP BP 5 …………………………………………………………9分 又BD2 3 BE  3 PE  BP2BE2  2 1 S  2 3 2  6 PBD 2 ……………………………………………………………11分 (3)设点C到平面PBD的距离为h V V PBCD CPBD 1 1 …………………………13分  S 1 S h 3 BCD 3 PBD 1 即 22 31= 6h 2 h= 2 …………………………15分 h 2 10 直线SC与平面PBD所成角的正弦值为   PC 5 5 …………………………17分 19.解：（1） 由余弦定理可知：BC2  AB2 AC2 2ABACcosBAC 1 即：BC2=25+9253 =19  2分 2 19 7 由题中定理可得：25+9=2(AD2  ),解得AD= 4 2 7 即三角形BC边上的中线长为 . 2 …………………………………………………………………… 4分 (2)证明： BC2 AB2AC2 法:1：在ABC中，cosB …………………………5分 2BCAB 1 BC2  AB2 AD2 在 ABD中， BD2  AB2 AD2 4 …………………………7分 cosB  2BDAB BCAB 1 cosB cosB,化简得AB2AC2 2AD2 BC2 2(AD2BD2)…………………9分 2 5 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#}AD2BD2 AB2 法2：在 ABD中cosADB , 2ADBD AD2 CD2  AC2 在ADC 中cosADC  2ADCD cosADBcosADC 0,化简得AB2  AC2  2(AD2 BD2) 法3：向量方法 AD是三角形BC边上的中线  1      AD (AB AC),BC  AC AB 2  2 1    2   ：AD = (AB AC)2，BC （AC AB）2 4 1     即：AD2  (AB2 AC2 2ABAC),BC2  AC2 AB2 2ABAC 4   4AD2  AB2 AC22ABAC  BC  4AD2BC2 2(AB2 AC2),即：AB2 AC2=2 AD2+（ )2    2  （3）解：(ⅰ)asin A3bsinB 3bsin(AC)，asin A=3b[sin(AC)sinB]， asin A=3b[sin(AC)sin（AC）],asin A=6bcosAsinC 设ABC的内角A,B,C的对边分别为a,b,c a2=6bccosA， b2 c2 a2 2 a2=6bc ，b2 c2  a2  24. …………………………12分 2bc 3 AB2  AC2  2(AD2 BD2),BD 3,所以AD  3 …………………………13分 1 3 3 S =2S =2 AD DC sin ADC = , ABC ADC 2 2 1  所以sinÐADC= ，即ÐADC= ， …………………………15分 2 6 AD2 CD2  AC2 在ADC 中，cosADC  ，得AC  3. …………………16分 2ADCD 2 在等腰ADC 中，ÐDAC= 3 1 所以cosDAC= …………………………17分 2 6 {#{QQABLYAAogioAIIAAQhCQQ0YCgIQkBAACSgOxBAEIAIAQQNABAA=}#}