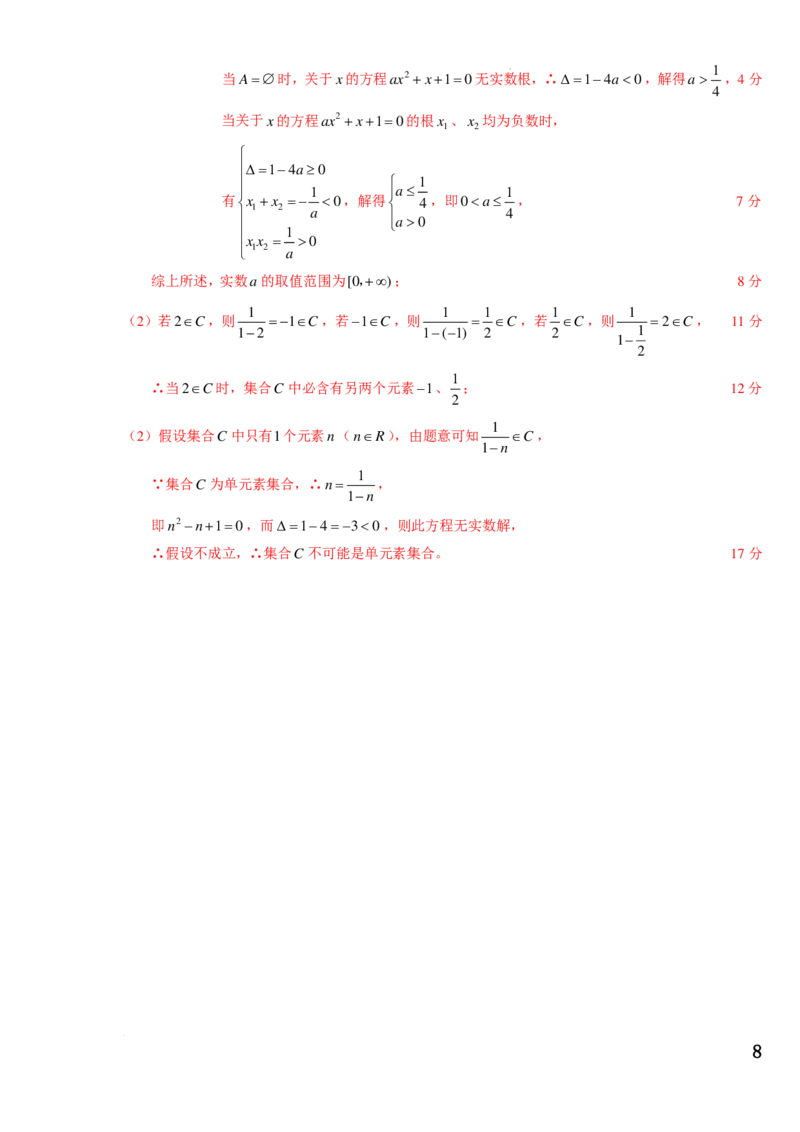数学答案-辽宁省名校联盟2024-2025学年高一上学期第一次月考_2024-2025高一（7-7月题库）_2024年9月试卷_0910辽宁省名校联盟2024-2025学年高一上学期第一次月考数学试题

绝 密★启用并使用完毕前 辽宁省名校联盟 2024-2025 学年高一第一次月考—数学 本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间120分钟 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。 1．给出下列关系式，其中正确的是（ ）。 A、0∈∅ B、{0}⊆{x|x2 =x} x+2y=5 C、{0}⊆ N D、{1，2}⊆{(x，y)| } + 3x−y=1 【答案】B 【解析】A选项，∅是没有任何元素的集合，错， B选项，∵{x|x2 =x}={0，1}，∴{0}⊆{x|x2 =x}，对， C选项，N 是正整数集合，错， + x+2y=5 D选项，{(x，y)| }={(1，2)}，元素是点坐标，错， 3x−y=1 故选B。 2．已知命题 p：∀x∈[0，+∞)，x2 +1≥1，则命题 p的否定为（ ）。 A、∃x∉[0，+∞)，x2 +1<1 B、∃x∈[0，+∞)，x2 +1<1 C、∀x∉[0，+∞)，x2 +1<1 D、∀x∈[0，+∞)，x2 +1≤1 【答案】B 【解析】命题 p：∀x∈[0，+∞)，x2 +1≥1否定为∃x∈[0，+∞)，x2 +1<1，故选B。 3．已知a、b、c∈R，则下列命题正确的是（ ）。 1 1 A、若ab≠0且a B、若0 ，错， a b B选项，0 ⋅[a⋅(a+1)]， a+1 a a+1 a ∴ab+a>ab+b，∴a>b与a0）。若命题q是命题 p的充分不必要条件，则实数 m的取值范围为（ ）。 1 1 1 4 1 4 A、(0，) B、(0，] C、( ，) D、[ ，] 3 3 3 3 3 3 【答案】B 【解析】由题意 p：|1−2x|≤5中，解得−2≤x≤3，在q：[x−(2+m)][x−(2−m)]≤0（m>0）中， −3m+2≥−2  解得−3m+2≤x≤3m+2，∵q是 p的充分不必要条件，∴3m+2≤3 ，等号不同时成立，  m>0 2 学科网（北京）股份有限公司1 1 ∴01）的解集为空集，则T = + 的最小值为（ ）。 a 2(ab−1) ab−1 A、 2 B、2 C、2 2 D、4 【答案】D 1 4c ab2 1 a(b+2c) 1+2ab+a2b2 【解析】 >0，b2 − ≤0，得c≥ ，∴T = + ≥ ， a a 4 2(ab−1) ab−1 2(ab−1) 1+2(m+1)+(m+1)2 m 2 令ab−1=m，则m>0，∴T ≥ = + +2≥4，故选D。 2m 2 m 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的得6分， 部分选对的得部分分，有选错的得0分。 9．已知集合P={(x，y)|x−y=0}、集合Q={(x，y)|x⋅y=1}，则下列说法正确的是（ ）。 A、PQ=R B、PQ={(1，1)，(−1，−1)} C、PQ={(x，y)|x=±1，y=±1} D、PQ有3个真子集 【答案】BD 1 【解析】由题意得集合P表示直线y=x上所有的点，集合Q表示y= 上所有的点，PQ是点集，A选项错， x y=x  x=1 x=−1 由 1 得 或 ，∴PQ={(1，1)，(−1，−1)}，∴B选项对，C选项错， y= y=1 y=−1  x ∴PQ有3个真子集：∅、{(1，1)}、{(−1，−1)}，D选项对， 故选BD。 10．已知条件 p：{x|x2 +x−6=0}，条件q：{x|mx+1=0}，且 p是q的必要条件，则实数m的值可以是（ ）。 1 1 1 A、− B、0 C、 D、 2 3 2 【答案】ABC 【解析】设集合A={x|x2 +x−6=0}={x|(x+3)(x−2)={−3，2}、集合B={x|mx+1=0}={x|mx=−1}， ∵ p是q的必要条件，∴B⊆ A， 当B=∅时，由mx+1=0无解可得m=0，符合题意， 1 当B≠∅时，B={2}或B={−3}，当B={2}时，由2m+1=0解得m=− ， 2 1 当B={−3}时，由−3m+1=0解得m= ， 3 1 1 综上所述，实数m的取值为0、− 、 ，故选ABC。 2 3 3 学科网（北京）股份有限公司x x+1 4x+a 11．已知关于x的方程 + = 只有一个实数根，则实数a的可能取值为（ ）。 x+1 x x(x+1) 1 A、 B、1 C、0 D、5 2 【答案】ABD x x+1 4x+a 【解析】对方程 + = ，去分母可得：2x2 −2x+1−a=0，且x≠−1且x≠0， x+1 x x(x+1) 此时∆=(−2)2 −4×2×(1−a)=8a−4， 1 1 当∆=0时，即a= 时，此时方程为2x2 −2x+ =0，即4x2 −4x+1=(2x−1)2 =0， 2 2 1 解得x= ，符合题意， 2 1 1− 2a−1 1+ 2a−1 当∆>0，即a> 时，方程2x2 −2x+1−a=0有两根x = 、x = >0， 2 1 2 2 2 当x =−1或x =0时，x 为增根，此时方程只有一个实根， 1 1 1 1− 2a−1 当x = =−1时，a=5，符合题意， 1 2 1− 2a−1 当x = =0时，a=1，符合题意， 1 2 1 综上所述，实数a的可能取值为 或1或5，故选ABD。 2 三、填空题：本题共3小题，每小题5分，共15分。 12．已知实数a满足：a+a−1 =3，则a3+a−3 = 。 【答案】18 【解析】a3 +a−3 =(a1+a−1)⋅(a2 +a1⋅a−1+a−2)=(a1+a−1)⋅[(a1+a−1)2 −3]=18。 b 13．若两个正实数a、b满足4a+b=ab，且存在这样的a、b使不等式a+ a+ 有解，则m2 +3m>4，即m2 +3m−4=(m+4)(m−1)>0， 4 4 学科网（北京）股份有限公司解得m<−4或m>1，∴实数m的取值范围为(−∞，−4)(1，+∞)。 x2 −2x−8>0 14．已知关于x的不等式组 仅有一个整数解，则实数k 的取值范围为 。  2x2 +(2k+7)x+7k <0 【答案】[−5，3)(4，5] 【解析】由不等式x2 −2x−8=(x+2)(x−4)>0，解得x<−2或x>4， 7 解方程2x2 +(2k+7)x+7k =0，解得x =− 、x =−k， 1 2 2 7 7 7 ①若−k <− ，即k > 时，不等式2x2 +(2k+7)x+7k <0的解集为(−k，− )， 2 2 2 若不等式组只有一个整数解，则−5≤k <−4，解得4− ，即k < 时，不等式2x2 +(2k+7)x+7k <0的解集为(− ，−k)， 2 2 2 若不等式组只有一个整数解，则−3<−k ≤5，解得−5≤k <3， 综上所述，实数k 的取值范围为[−5，3)(4，5]。 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（本小题满分13分）某光伏企业投资144万元用于太阳能发电项目，经计算n（n∈N∗）年内的总维修保养费用为 4n2 +20n万元，该项目每年可给公司带来100万元的收入。假设到第n年年底，该项目的纯利润为y万元。（纯利润= 累计收入-总维修保养费用−投资成本） （1）写出纯利润y的表达式，并求该项目从第几年起开始盈利； （2）若干年后，该公司为了投资新项目，决定转让该项目，现有以下两种处理方案： ①年平均利润最大时，以72万元转让该项目；②纯利润最大时，以8万元转让该项目； 你认为以上哪种方案最有利于该公司的发展？请说明理由。 【解析】（1）由题意可知y=100n−(4n2 +20n)−144=−4n2 +80n−144（n∈N∗）， 2分 令y>0，即−4n2 +80n−144>0，即n2 −20n+36=(n−2)(n−18)>0，解得20、y>0，∴x+ y≥2 xy ，又∵x+ y=4，∴4≥2 xy ，∴x⋅y≤4， ∴不存在x、y使得x⋅y=5； 5分 （2）(a2 +b2)(c2 +d2)≥(ac+bd)2，证明如下： (a2 +b2)(c2 +d2)−(ac+bd)2 =a2d2 +b2c2 −2abcd =(ad −bc)2 ≥0， 当且仅当ad =bc时等号成立，∴(a2+b2)(c2 +d2)≥(ac+bd)2； 10分 （3）由（1）得(22 +12)(m2 +n2)≥(2m+n)2，∴(2m+n)2 ≤5×5=25，∴2m+n≤5， 当且仅当m=2n，即m=2、n=1时等号成立，∴2m+n的最大值为5。 15分 17．（本小题满分15分）根据要求完成下列问题： x−4 （1）已知命题 p： <0，命题q：x2 −(a+1)x+a<0（a∈R），且命题 p是命题q的必要不充分条件，求实数a x+3 的取值范围。 （2）已知不等式|2x−1|<2的解集与关于x的不等式−x2 − px+q>0（ p、q∈R）的解集相同，若实数a，b∈R 满 + 1 4 足a+b= p+4q，求 + 的最小值。 a b x−4 【解析】（1）命题 p： <0，解得−31时，解得10得x2 + px−q<0，其解集为− 0且∆=16(1−k)2 −12(k2 +4k−5)<0， 即(k+5)(k−1)>0且(k−1)(k−19)<0，解得10，解得m≤−2 3−2或m≥2 3−2， ∴m≤−2 3−2或2 3−2≤m<2， 10分 m 1 根据韦达定理得x +x = 、x ⋅x =− ， 11分 1 2 m−2 1 2 m−2 m 4 m2 +4m−8 又∵1≤|x −x |≤3，∴1≤(x +x )2 −4x ⋅x ≤3，∴1≤( )2 + = ≤3， 1 2 1 2 1 2 m−2 m−2 m2 −4m+4 3 3 5− 3 ∴m≥ 且m2 −8m+10≥0，∴ ≤m≤ ， 16分 2 2 2 3 5− 3 3 5− 3 综上所述， ≤m≤ ，∴实数m的取值范围为[ ， ]。 17分 2 2 2 2 19．（本小题满分17分）根据要求完成下列问题： （1）已知集合A={x|ax2 +x+1=0}、集合B={x|x≥0}，且满足AB=∅，求实数a的取值范围； 1 （2）设数集C 满足：1∉C，又若实数m是数集C 中的一个元素，则 一定也是数集C 中的一个元素，求证： 1−m ①若2∈C，则集合C 中还有其他两个元素； ②集合C 不可能是单元素集合。 【解析】（1）当a=0时，A={x|x+1=0}={−1}，此时AB=∅， 1分 当a≠0时，∵AB=∅，∴A=∅或关于x的方程ax2 +x+1=0的根均为负数， 2分 7 学科网（北京）股份有限公司1 当A=∅时，关于x的方程ax2 +x+1=0无实数根，∴∆=1−4a<0，解得a> ，4分 4 当关于x的方程ax2 +x+1=0的根x 、x 均为负数时， 1 2  ∆=1−4a≥0   1  1 a≤ 1 有x +x =− <0，解得 4，即00 4  1 xx = >0  1 2 a 综上所述，实数a的取值范围为[0，+∞)； 8分 1 1 1 1 1 （2）若2∈C，则 =−1∈C，若−1∈C，则 = ∈C ，若 ∈C，则 =2∈C， 11分 1−2 1−(−1) 2 2 1 1− 2 1 ∴当2∈C时，集合C 中必含有另两个元素−1、 ； 12分 2 1 （2）假设集合C 中只有1个元素n（n∈R），由题意可知 ∈C， 1−n 1 ∵集合C 为单元素集合，∴n= ， 1−n 即n2−n+1=0，而∆=1−4=−3<0，则此方程无实数解， ∴假设不成立，∴集合C 不可能是单元素集合。 17分 8 学科网（北京）股份有限公司