数学答案-湖南省株洲市天元区株洲市二中2023级高一年级暑期夏令营检测试卷_2024-2025高一（7-7月题库）_2024年8月试卷_0813湖南省株洲市天元区株洲市二中2023级高一年级暑期夏令营检测

株洲市二中 2023 级高一年级暑期夏令营检测试卷 数学试题 命题人：金 晶 审题人：杨平安 时量：120 分钟 分值：150分 一、单选题(本大题共8个小题，每小题5分，共60分，在每小题给出的四个选项中只有一 个是符合题目要求的) 1．在一些美术字中，有的汉字是轴对称图形.下面4个汉字中，可看作是轴对称图形的是（ ） A．全 B．面 C．发 D．展 1．A 【分析】根据轴对称的定义判断即可； 【详解】解：全面发展四个字中，可以看作是轴对称图形的是全； 故选A． 2．四个大小相同的正方体搭成的几何体如图所示，从正面得到的视图是（ ） A． B． C． D． 2．D 【分析】根据从正面看得到的图形是主视图，可得答案． 【详解】从正面看第一层是2个小正方形，第二层右边1个小正方形， 故选：D． 【点睛】考查了简单组合体的三视图，从正面看得到的图形是主视图． 4 3．反比例函数y 的图象一定经过的点是（ ） x A．1，4 B．1，4 C．2，2 D．2，2 3．C 4 【分析】根据题意将各项的坐标代入反比例函数y 即可解答． x 4 【详解】解：A、将x1代入反比例函数y 得到y14，故A项不符合题意； x {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}4 B、项将x1代入反比例函数y 得到y44，故B项不符合题意； x 4 C、项将 代入反比例函数y 得到y2，故C项符合题意； x =−2 4 4 D、项将x2代入反比例函数y y 得到y22，故D项不符合题意； x x 故选C． 【点睛】本题考查了反比例函数图象上点的坐标特征，只要点在函数图象上则其坐标一定满 足函数解析式，掌握反比例函数图象上点的坐标特征是解题的关键． 4.若 ，则实数 的值为 ( ) 2 A．1∈ { +2, } B． C． 或 D． 或 答案 −1 1 1 −1 1 3 解析 由 ，可得 ，则 ． 2 2 当 1∈ {时 +，2, } ，满 足=要1求， =±1 当 =1 时， +2=3 ，不满足元素的互异性， =−．1 −1+2= 1 ∴故 选=：1 ． 5．“ m 1” 是“方程x2mx10无实数解”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】A 【分析】根据一元二次方程根的情况，由判别式即可得2m2，由集合间的关系即可求 解. 【详解】方程x2mx10无实数解,则需满足m240，解得2m2， m 11m1，由于  x 1m1  x 2m2  ，所以“ m 1”是“方程x2mx10  无实数解”的充分不必要条件， 故选：A 6．已知 ，则集合 的子集的个数是( ) 6 ． ={ ∈ |6− ∈ ． } ． ． 答案 8 16 32 64 解析 由于 ，则 ． ∈ =0,1,2,3,… {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}当 时， ，当 时， ， 6 6 6 =0 6−0=1 ∈ =1 6−1=5∉ 当 时， ，当 时， 6 3 6 6 =2 6−2=2∉ =3 6−3=3=2 ∈ , 当 时， ，当 时， ， 6 6 6 =4 6−4=2=3 ∈ =5 6−5=6 ∈ 当 时， 6 故集 = 合 7 集合 6−7=−1∉ ， 所 ,… 以集合 子集个数为 个． 4 故选： ． ={0,3,4,5} 2 =16 7．皮克定理 是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 ，其中N，L分别表示这个多边形内部与边界上的格点个数．在平面直角 1 S N L1 2 坐标系中，横、纵坐标都是整数的点为格点．已知A(0,30)，B(20,10)，O(0,0),则△ABO内部 的格点个数是 A．266 B．270 C．271 D．285 【答案】C 8．已知集合Ak1,k2,,kn，k，n为正整数，若集合 A 中所有元素之和为2019， 则当n取最大值时，集合 A 中最大的元素是( ) A．338 B．339 C．673 D．674 【答案】B 【解析】由题意利用等差数列的前n项和公式，分类讨论n，得出结论. 【详解】集合Ak1,k2,,kn， k，n为正整数， A中共有n个正整数，且这n个正整数从小到大排列，构成以k+1为首项，以1为公差的 等差数列. n(n1) 2kn1 若集合A中所有元素之和为n(k1)  n20193673 ， 2 2 当n为偶数时，设n=2m，m为正整数，(2k2m1)m3673， m=3，2k+2m＋1=673,即m=3，n=6，k=333， 即m3,n6,k 333. 当n为奇数时，设n2m1，m为正整数，(km1)(2m1)3673， 2m13,km1673， {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}即m1,n3,k 671， 故n的最大值为6，此时A334,335,336,337,338,339 . 二、多项选择题（本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多 项符合题目要求.全部选对得5分，有选错的得0分，部分选对的得2分） 9．下列说法正确的是（ ） A．8的相反数是8 B．a6a2 a3 C．在平面直角坐标系中，点P(2,3)关于x轴对称的点P的坐标是(2,3) D．(7)(5)的结果是2 【答案】CD 10．非空集合G关于运算满足：（1）对任意a，bG，都有abG；（2）存在eG， 使得对一切aG，都有aeeaa，则称G关于运算为“融洽集”.现给出下列集合和 运算，其中G关于运算为“融洽集”的是（ ） A．G有理数 ，为实数的乘法 B．G非负整数 ，为整数的加法 C．G偶数 ，为整数的乘法 D．G二次三项式，为多项式的加法 【答案】AB 【分析】根据G是关于运算⊕为“融洽集”的定义，逐一分析四个集合及运算是否满足定义， 可得答案． 【详解】对于A，G有理数 ，为实数的乘法满足（1），且存在e1满足（2），故G 是关于运算⊕的融洽集，A正确， 对于B，G{非负整数}，为整数的加法满足（1），且存在e0满足（2），故G是关于 运算⊕的融洽集，正确， 对于C，G{偶数}，为整数的乘法，若存在e满足（2），则e1为奇数，与已知矛盾， 故G不是关于运算⊕的融洽集，错误， 对于D，G二次三项式，为多项式的加法．两个二次三项式的和不一定是二次三项式， 不满足（1），故G不是关于运算⊕的融洽集，错误， 故选：AB． 11．如图，在Rt△ABC中，C90，AC6，AB10 ，以点A为圆心，适当长为半径画 {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}1 弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于 MN的长为半径画弧，两 2 弧在CAB的内部相交于点P，画射线AP与BC交于点D，DEAB，垂足为E．则下列 结论正确的是（ ） A．CADBAD B．CDDE C．AD5 3 D．CD:BD3:5 【答案】ABD 【分析】由作图方法可知，AD是BAC的角平分线，则由角平分线的定义和性质即可判定 A、B；利用勾股定理求出BC，利用等面积法求出CD3，由此求出AD、BD即可判断C、 D． 【详解】解：由作图方法可知，AD是BAC的角平分线， ∴CADBAD，故A结论正确； ∵C 90，DE⊥AB， ∴CDDE，故B结论正确； 在Rt△ABC中，由勾股定理得 BC AB2AC2 8 ， ∵S  S S ， △ABC △ACD △BAD 1 1 1 ∴ ACBC CDAC ABDE， 2 2 2 1 1 1 ∴ 68 6CD 10CD， 2 2 2 ∴CD3， ∴ AD AC2CD2 3 5，BD BCCD5 ，故C结论错误； ∴CD:BD3:5，故D结论正确. 12．抛物线yax2bxca0的图象如图所示，对称轴为直线x2．下列说法中正确 是（ ） A．abc0 B．c3a0 C．4a22ab≥atatb（t为全体实数） D．若图象上存在 {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}点Ax ,y 和点Bx ,y ，当mx x m3时，满足y  y ，则m的取值范围为 1 1 2 2 1 2 1 2 5m2． 【答案】ABD 【分析】开口方向，对称轴，与y轴的交点位置判断①，特殊点判断②，最值判断③，对称 性判断④即可． b 【详解】∵抛物线的开口向下，对称轴为直线x 20，抛物线与y轴交点位于负 2a 半轴， ∴a0,b0,c0， ∴abc0， 故A正确； 由图象可知，abc0，根据对称轴，得b4a， ∴a4ac0 ∴c3a0， 故B正确； b ∵抛物线的开口向下，对称轴为直线x 20， 2a ∴抛物线的最大值为y4a2bc， 当xt时，其函数值为yat2btc， ∴4a2bcat2btc， ∴4a2bat2bt ， ∵a0， ∴a4a2b≤a at2bt  ， {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}∴4a22ab≤atatb， 故C错误； 如图所示，Ax ,y 和点Bx ,y 满足y  y ， 1 1 2 2 1 2 ∴Ax ,y 和点Bx ,y 关于对称轴对称， 1 1 2 2 ∴x 2,x 2, 1 2 ∵m x  x m3, 1 2 ∴m x 2,2 x m3, 1 2 解得5m2， 故D正确； 【点睛】本题考查了二次函数的图象和性质，熟练掌握二次函数的性质，是解题的关键． 三、填空题（本大题共4小题，每小题5分，共20分） 13．设全集U＝R，集合A＝{x|0≤x≤2}，B＝{y|1≤y≤3}，则( A)∪B＝__________． ∁ U 【答案】{x|x<0或x≥1} 【解析】因为 A＝{x|x>2或x<0}，B＝{y|1≤y≤3}，所以( A)∪B＝{x|x<0或x≥1}． ∁ U ∁ U 1 14.已知x2 3x10，则x3  7的值为_______. x3 【答案】25 15．用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图 案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，……，按此规 律排列下去，则第⑧个图案用的木棍根数是（ ） {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}【答案】44 【分析】根据各图形中木棍的根数发现计算的规律，由此即可得到答案． 【详解】解：第①个图案用了459根木棍， 第②个图案用了45214根木棍， 第③个图案用了45319根木棍， 第④个图案用了45424根木棍， ……， 第⑧个图案用的木棍根数是45844根， 1 16．如图，BAC 90,AB AC 3 2．过点C作CDBC，延长CB到E，使BE  CD， 3 连接AE,ED．若ED2AE，则BE________________．（结果保留根号） 16． 71/1 7 【分析】如图，过E作EQCQ于Q，设BE  x,AE  y，可得CD3x,DE2y，证明 BC 2AB6，CE6x，△CQE为等腰直角三角形， 2 2 2 2 QE CQ CE  6x  3 2 x ，AQ x ，由勾股定理可得： 2 2 2 2 2y2 6x23x2     2  2  2  2 ，再解方程组可得答案． y2  x 3 2 x       2   2  【详解】解：如图，过E作EQCQ于Q， 设BE  x,AE  y， {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}1 ∵BE  CD，ED2AE， 3 ∴CD3x,DE2y， ∵BAC 90,AB AC 3 2， ∴BC 2AB6，CE6x，△CQE为等腰直角三角形， 2 2 2 ∴QE CQ CE  6x  3 2 x ， 2 2 2 2 ∴AQ x ， 2 2y2 6x23x2   由勾股定理可得：  2  2  2  2 ， y2  x 3 2 x       2   2  整理得：x2 2x60， 解得：x1 7， 经检验x1 7不符合题意； ∴BEx1 7； 故答案为：1 7． 四、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） 17．不等式x2 3x20的解集记为p，关于x的不等式x2  a1  xa 0的解集记为 q，若p是q的充分不必要条件，求实数a的取值范围． 【答案】2 a  1． 【解析】由不等式x2 3x20，得x2或x1， 不等式x2  a1  xa 0等价为 x1  xa 0， ①当a 1，即a  1时，不等式的解是x 1或xa， ∵p是q的充分不必要条件，∴a 1，即a  1； ②若a 1，即a  1时，不等式的解是xa或x 1， ∵p是q的充分不必要条件，∴a2，即2 a  1， 综上2 a  1． 18．设集合Ax|2x5,Bx|m1x2m1, {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}(1)若m4，求AB； (2)若BIAB ，求实数m的取值范围． 【答案】(1)ABx|2x7 ; (2) ,3  . 【分析】（1）根据并集的定义运算即得； （2）由题可得BA，分类讨论进而可得不等式即得. 【详解】（1）当m4时，Bx|5x7，Ax|2x5,ABx|2x7； （2）BAB,B A， 当B时，满足题意，此时m1＞2m1，解得m＜2； 2m1  当B时，2m15 解得2m3，  m12m1  实数m的取值范围为,3  . 19．为了解A、B两款品质相近的智能玩具飞机在一次充满电后运行的最长时间，有关人员 分别随机调查了A、B两款智能玩具飞机各10架，记录下它们运行的最长时间（分钟），并 对数据进行整理、描述和分析（运行最长时间用x表示，共分为三组：合格60x70，中 等70x80，优等x80），下面给出了部分信息： A款智能玩具飞机10架一次充满电后运行最长时间是： 60,64,67,69,71,71,72,72,72,82 B款智能玩具飞机10架一次充满电后运行最长时间属于中等的数据是： 70,71,72,72,73 两款智能玩具飞机运行最长时间统计表，B款智能玩具飞机运行最长时间扇形统计图 类别 A B 平均数 70 70 中位数 71 b {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}众数 a 67 方差 30.4 26.6 根据以上信息，解答下列问题： (1)上述图表中a___________，b___________，m___________； (2)根据以上数据，你认为哪款智能玩具飞机运行性能更好？请说明理由（写出一条理由即 可）； (3)若某玩具仓库有A款智能玩具飞机200架、B款智能玩具飞机120架，估计两款智能玩具 飞机运行性能在中等及以上的共有多少架？ 20．(1)72，70.5，10； (2)B款智能玩具飞机运行性能更好；因为B款智能玩具飞机运行时间的方差比A款智能玩 具飞机运行时间的方差小，运行时间比较稳定； (3)两款智能玩具飞机运行性能在中等及以上的大约共有192架． 【分析】（1）由A款数据可得A款的众数，即可求出a，由B款扇形数据可求得合格数及 优秀数，从而求得中位数及优秀等次的百分比； （2）根据方差越小越稳定即可判断； （3）用样本数据估计总体，分别求出两款飞机中等及以上的架次相加即可． 【详解】（1）解：由题意可知10架A款智能玩具飞机充满电后运行最长时间中，只有72出 现了三次，且次数最多，则该组数据的众数为72，即a72； 由B款智能玩具飞机运行时间的扇形图可知，合格的百分比为40%， 则B款智能玩具飞机运行时间合格的架次为：1040%4（架） 则B款智能玩具飞机运行时间优等的架次为：10451（架） 则B款智能玩具飞机的运行时间第五、第六个数据分别为：70,71， 7071 故B款智能玩具飞机运行时间的中位数为： 70.5 2 {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}1 B款智能玩具飞机运行时间优等的百分比为： 100%10% 10 即m10 故答案为：72，70.5，10； （2）B款智能玩具飞机运行性能更好；因为B款智能玩具飞机运行时间的方差比A款智能 玩具飞机运行时间的方差小，运行时间比较稳定； （3）200架A款智能玩具飞机运行性能在中等及以上的架次为： 6 200 120（架） 10 200架A款智能玩具飞机运行性能在中等及以上的架次为： 6 120 72（架） 10 则两款智能玩具飞机运行性能在中等及以上的共有：12072192架， 答：两款智能玩具飞机运行性能在中等及以上的大约共有192架． 20．(12分)如图，一次函数y2x的图象与反比例函数y k (x0)的图象交于点A4,n．将 x 点A沿x轴正方向平移m个单位长度得到点B,D为x轴正半轴上的点，点B的横坐标大于点 k D的横坐标，连接BD,BD的中点C在反比例函数y (x0)的图象上． x (1)求n,k的值； (2)当m为何值时，ABOD的值最大?最大值是多少? 20．(1)n8，k 32 (2)当m6时，ABOD取得最大值，最大值为36 【分析】（1）把点A4,n代入y2x，得出n8，把点A4,8代入y k (x0)，即可求得 x k 32； {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}（2）过点C作x轴的垂线，分别交AB,x轴于点E,F，证明△ECB≌△FCD，得出 BE DF,CE CF ，进而可得C(8,4)，根据平移的性质得出B(m4,8)，D(12m,0)，进而 表示出ABOD，根据二次函数的性质即可求解． 【详解】（1）解：把点A4,n代入y2x， ∴n24， 解得：n8； 把点A4,8代入y k (x0)，解得k 32； x （2）∵点B横坐标大于点D的横坐标， ∴点B在点D的右侧， 如图所示，过点C作x轴的垂线，分别交AB,x轴于点E,F， ∵AB∥DF ， ∴BCDF ， 在ECB和FCD中， BCEDCF  BC CD ，  BCDF ∴ECB≌FCDASA， ∴BE DF,CE CF ， ∵EF  y 8， A ∴CECF 4， ∴C(8,4)， ∵将点A沿x轴正方向平移m个单位长度得到点B， ∴B(m4,8)， ∴BEDF m4， {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}∴D(12m,0)， ∴OD12m， ∴ABODm12mm6236， ∴当m6时，ABOD取得最大值，最大值为36． 【点睛】本题考查了一次函数与反比例函数综合，二次函数的性质，全等三角形的性质与判 定，熟练掌握以上知识是解题的关键． 21．如图，已知O是Rt△ABC的外接圆，ACB90，D是圆上一点，E是DC延长线 上一点，连结AD，AE，且ADAE，CACE ． (1)求证：直线AE是O是的切线； 2 (2)若sinE ，O的半径为3，求AD的长． 3 21．(1)见解析 8 5 (2) 3 【分析】（1）由ACB90，可知AB是O的直径，由 A  C A  C ，可得ABC ADC， 由ADAE，CACE，可得EADC，CAE E，则CAE ADC ABC，由 ABCCAB90，可得CAECAB90，即OAE90，进而结论得证； 1 （2）作CF  AE，垂足为E，如图所示，由题意知，△ACE是等腰三角形，则EF  AE， 2 2 由题意知，AB6，sinABC sinE，可求AC ABsinB6 4，CE4， 3 2 8 4 5 CF CEsinE 4  ，由勾股定理得EF  CE2CF2  ，根据ADAE 2EF ， 3 3 3 计算求解即可． 【详解】（1）证明：∵ACB90， ∴AB是O的直径， {#{QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}∵ ， AC AC ∴ABC ADC， ∵ADAE，CACE， ∴EADC，CAE E， ∴CAE ADC ABC， ∵ABCCAB90， ∴CAECAB90， ∴OAE90， 又∵OA是半径， ∴直线AE是O是的切线； （2）解：作CF  AE，垂足为E，如图所示， ∵CACE， ∴△ACE是等腰三角形， ∵CF  AE， 1 ∴EF  AE， 2 由题意知，AB6，sinABC sinE， 2 ∴AC ABsinB6 4， 3 ∴CE4， 2 8 ∴CF CEsinE 4  ， 3 3 4 5 由勾股定理得EF  CE2CF2  ， 3 8 5 ∴ADAE  2EF  ， 3 8 5 ∴AD的长为 ． 3 {#{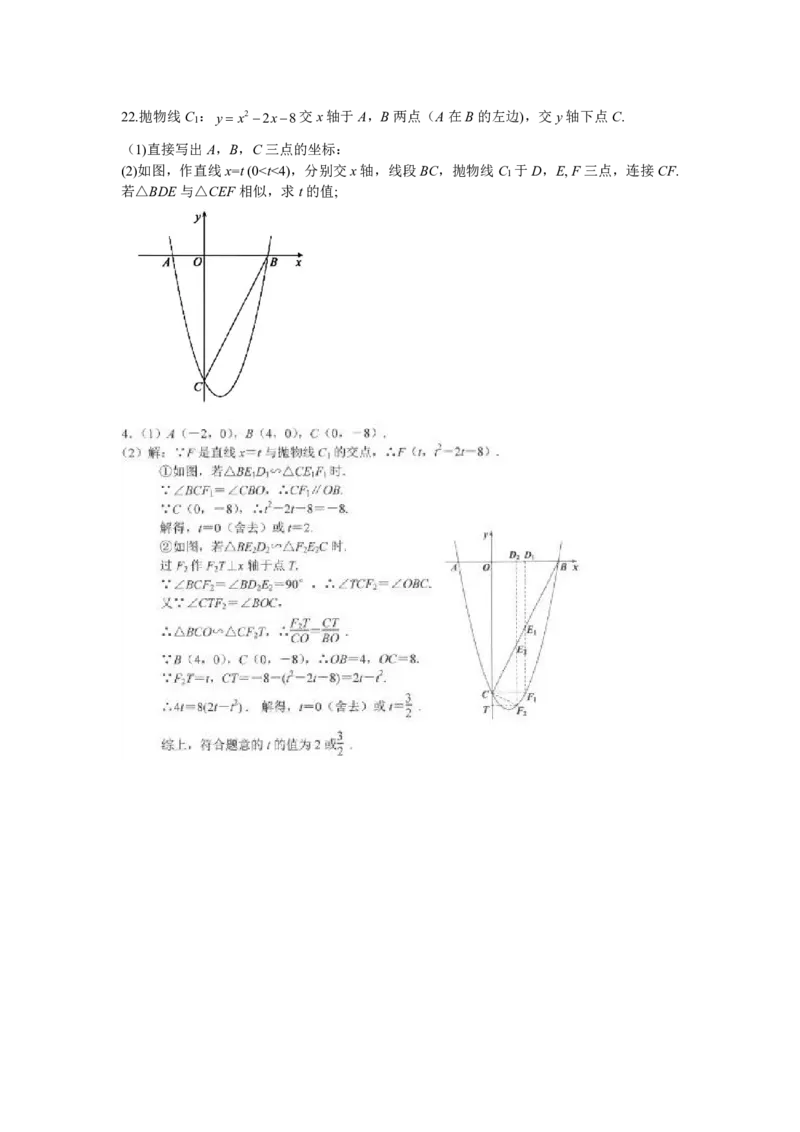QQABDQIEggCgABJAABhCUQHwCEKQkAACAIgOBFAAMAAACRNABAA=}#}22.抛物线C 1 ：y x22x8交x轴于A，B两点（A在B的左边)，交y轴下点C. （1)直接写出A，B，C三点的坐标： (2)如图，作直线x=t(0