文档内容
安徽六校教育研究会 2024 级高一新生入学素质测试
数学试题
2024.8
注意事项:
1.本试卷满分 100分,考试时间 120分钟.
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
3.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷
上无效.
4.考试结束后,将本试卷和答题卡一并交回.
一、单选题(共 10小题,每小题 3分,共 30分)
1.下列各数中,比−2大的数是( )
A.−2 3 B.−2 2 C.− 6 D.− 3
2.下列运算正确的是( )
( )3 ( )2
A. n3 =n6 B. −2a2 =−4a4 C.x8 ÷x2 = x4 D.m2⋅m=m3
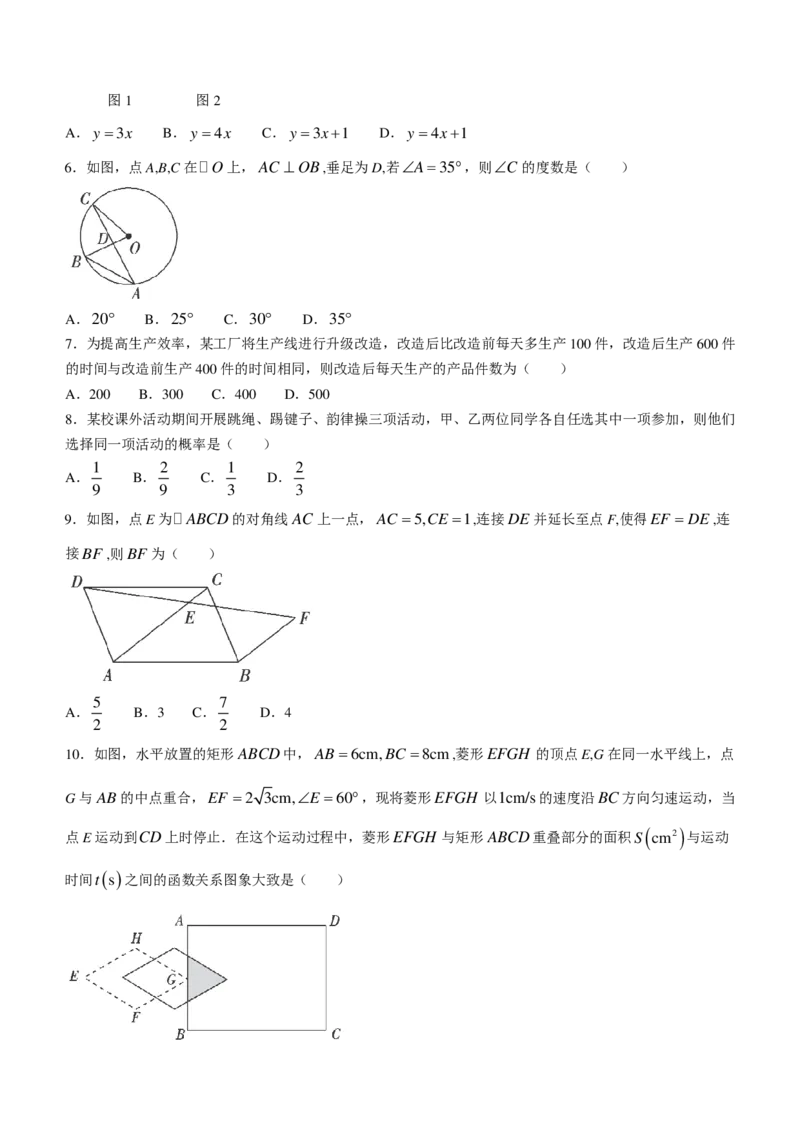
3.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ABD=60°,AB =2,则AC的长为( )
A.6 B.5 C.4 D.3
4.目前全球最薄的手撕钢产自中国,厚度只有0.015毫米,约是A4纸厚度的六分之一.已知1毫米=1百万
纳米,0.015毫米等于多少纳米?将结果用科学记数法表示为( )
A.1.5×103纳米 B.1.5×104纳米 C.1.5×10−5纳米 D.1.5×10−6纳米
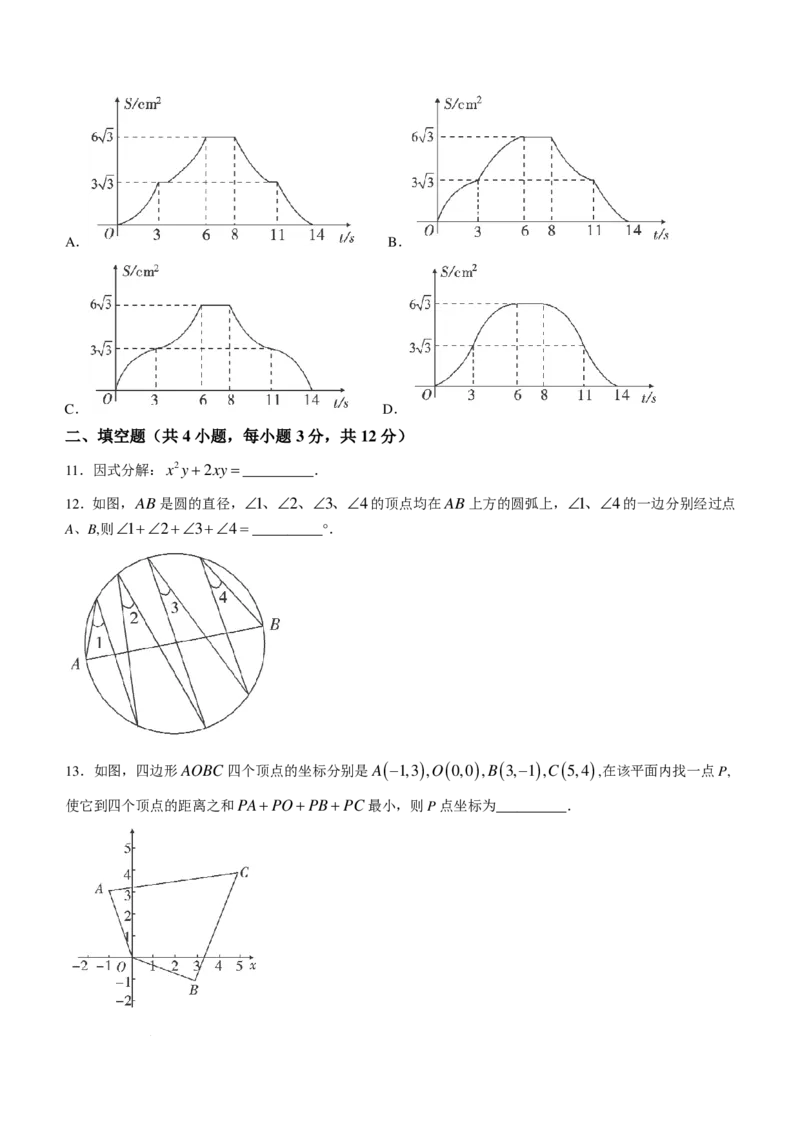
5.如图1,“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七
张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如
图2给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为x尺,长桌的长为y尺,则y
与x的关系可以表示为( )
学科网(北京)股份有限公司图1 图2
A.y =3x B.y =4x C.y =3x+1 D.y =4x+1
6.如图,点A,B,C在 O上,AC ⊥OB,垂足为D,若∠A=35°,则∠C 的度数是( )
A.20° B.25° C.30° D.35°
7.为提高生产效率,某工厂将生产线进行升级改造,改造后比改造前每天多生产100件,改造后生产600件
的时间与改造前生产400件的时间相同,则改造后每天生产的产品件数为( )
A.200 B.300 C.400 D.500
8.某校课外活动期间开展跳绳、踢键子、韵律操三项活动,甲、乙两位同学各自任选其中一项参加,则他们
选择同一项活动的概率是( )
1 2 1 2
A. B. C. D.
9 9 3 3
9.如图,点E为 ABCD的对角线AC上一点,AC =5,CE =1,连接DE并延长至点F,使得EF = DE,连
接BF ,则BF 为( )
5 7
A. B.3 C. D.4
2 2
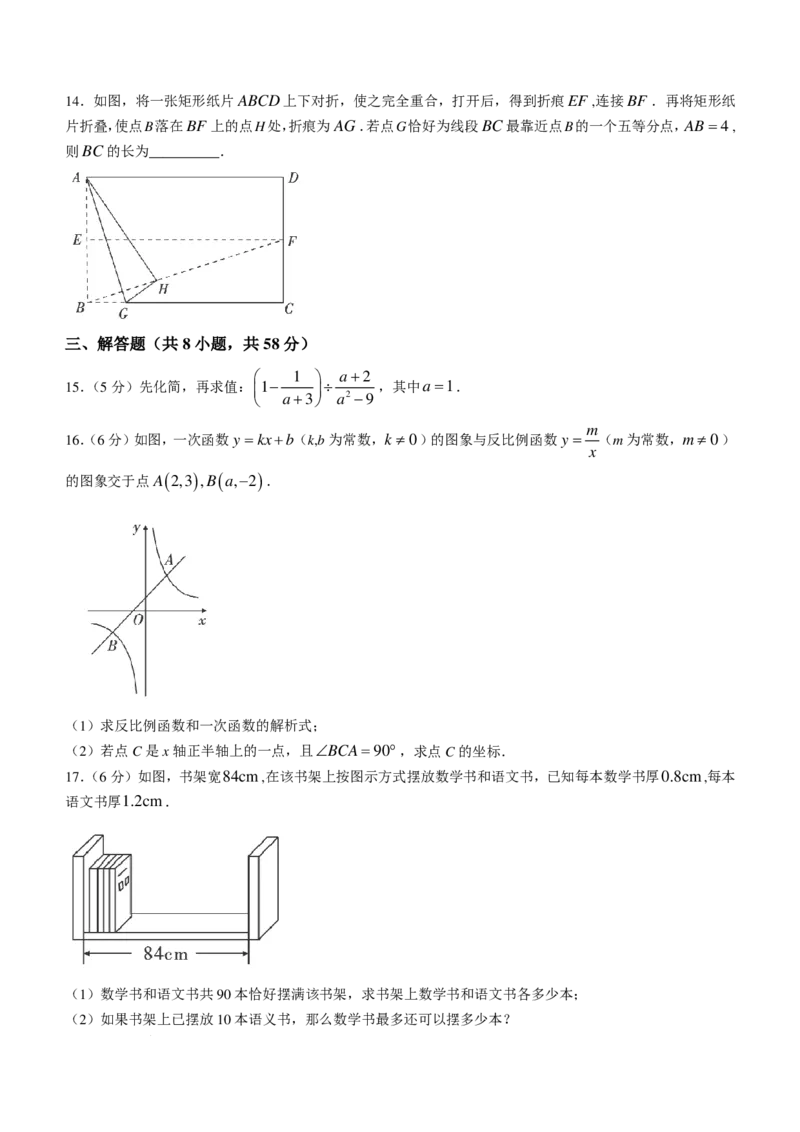
10.如图,水平放置的矩形ABCD中,AB=6cm,BC =8cm,菱形EFGH 的顶点E,G在同一水平线上,点
G与AB的中点重合,EF =2 3cm,∠E =60°,现将菱形EFGH 以1cm/s的速度沿BC方向匀速运动,当
( )
点E运动到CD上时停止.在这个运动过程中,菱形EFGH 与矩形ABCD重叠部分的面积S cm2 与运动
时间t ( s )之间的函数关系图象大致是( )
学科网(北京)股份有限公司A. B.
C. D.
二、填空题(共 4小题,每小题 3分,共 12分)
11.因式分解:x2y+2xy =__________.
12.如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点
A、B,则∠1+∠2+∠3+∠4=__________°.
13.如图,四边形AOBC四个顶点的坐标分别是A (−1,3 ) ,O ( 0,0 ) ,B ( 3,−1 ) ,C ( 5,4 ) ,在该平面内找一点P,
使它到四个顶点的距离之和PA+PO+PB+PC最小,则P点坐标为__________.
学科网(北京)股份有限公司14.如图,将一张矩形纸片ABCD上下对折,使之完全重合,打开后,得到折痕EF ,连接BF .再将矩形纸
片折叠,使点B落在BF 上的点H处,折痕为AG.若点G恰好为线段BC最靠近点B的一个五等分点,AB =4,
则BC的长为__________.
三、解答题(共 8小题,共 58分)
1 a+2
15.(5分)先化简,再求值: 1−
÷ ,其中a =1.
a+3 a2 −9
m
16.(6分)如图,一次函数y =kx+b(k,b为常数,k ≠0)的图象与反比例函数y = (m为常数,m≠0)
x
的图象交于点A ( 2,3 ) ,B ( a,−2 ).
(1)求反比例函数和一次函数的解析式;
(2)若点C是x轴正半轴上的一点,且∠BCA=90°,求点C的坐标.
17.(6分)如图,书架宽84cm,在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚0.8cm,每本
语文书厚1.2cm.
(1)数学书和语文书共90本恰好摆满该书架,求书架上数学书和语文书各多少本;
(2)如果书架上已摆放10本语义书,那么数学书最多还可以摆多少本?
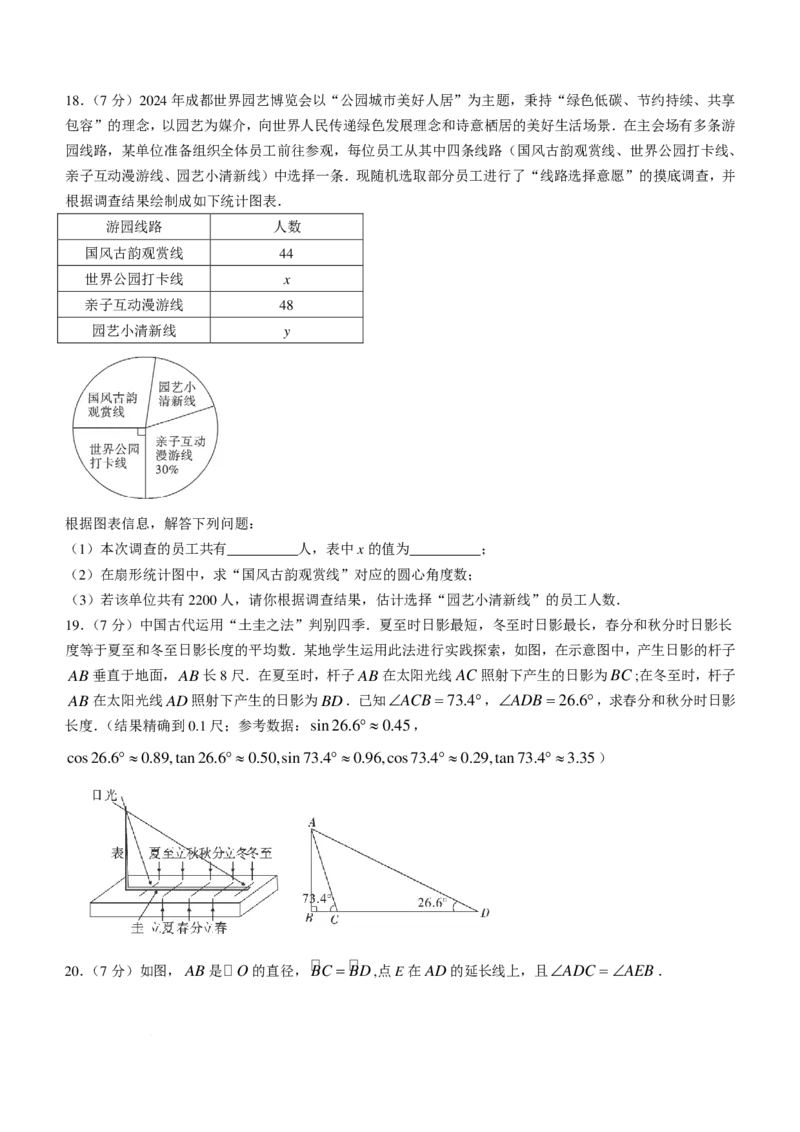
学科网(北京)股份有限公司18.(7分)2024年成都世界园艺博览会以“公园城市美好人居”为主题,秉持“绿色低碳、节约持续、共享
包容”的理念,以园艺为媒介,向世界人民传递绿色发展理念和诗意栖居的美好生活场景.在主会场有多条游
园线路,某单位准备组织全体员工前往参观,每位员工从其中四条线路(国风古韵观赏线、世界公园打卡线、
亲子互动漫游线、园艺小清新线)中选择一条.现随机选取部分员工进行了“线路选择意愿”的摸底调查,并
根据调查结果绘制成如下统计图表.
游园线路 人数
国风古韵观赏线 44
世界公园打卡线 x
亲子互动漫游线 48
园艺小清新线 y
根据图表信息,解答下列问题:
(1)本次调查的员工共有__________人,表中x的值为__________;
(2)在扇形统计图中,求“国风古韵观赏线”对应的圆心角度数;
(3)若该单位共有2200人,请你根据调查结果,估计选择“园艺小清新线”的员工人数.
19.(7分)中国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长
度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图,在示意图中,产生日影的杆子
AB垂直于地面,AB长8尺.在夏至时,杆子AB在太阳光线AC照射下产生的日影为BC;在冬至时,杆子
AB在太阳光线AD照射下产生的日影为BD.已知∠ACB=73.4°,∠ADB=26.6°,求春分和秋分时日影
长度.(结果精确到0.1尺;参考数据:sin26.6°≈0.45,
cos26.6°≈0.89,tan26.6°≈0.50,sin73.4°≈0.96,cos73.4°≈0.29,tan73.4°≈3.35)
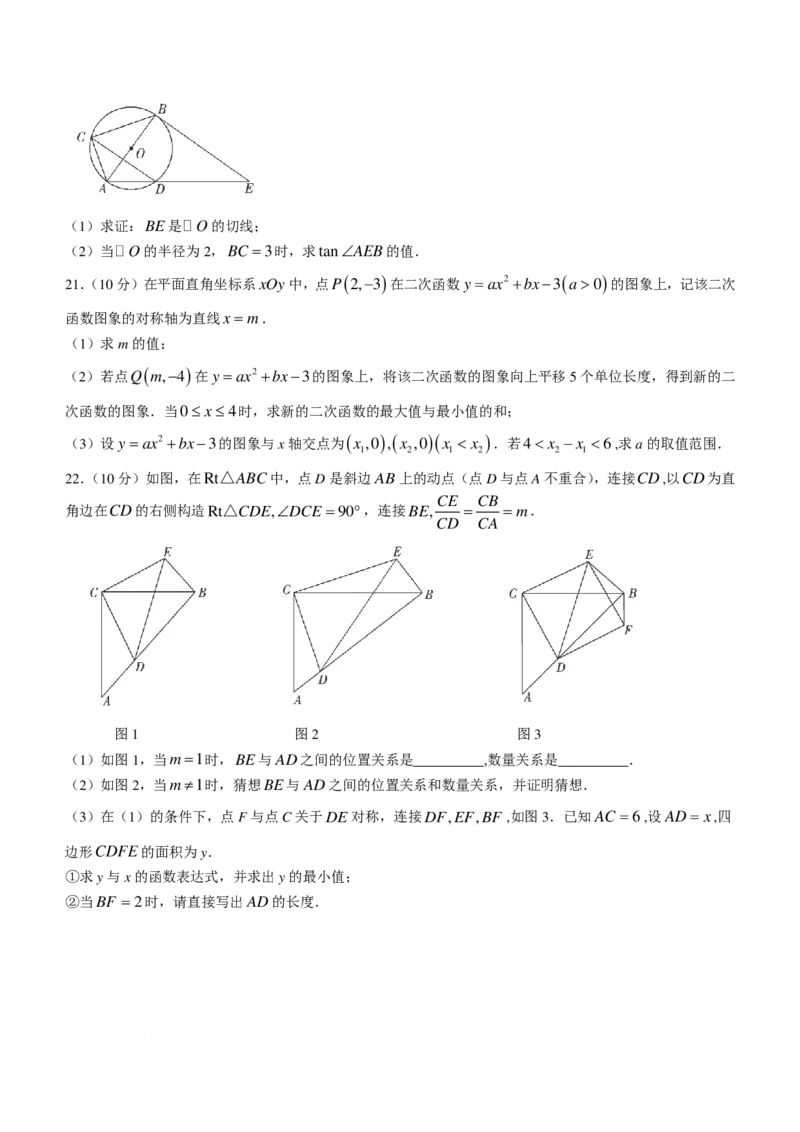
20.(7分)如图,AB是 O的直径,BC = BD,点E在AD的延长线上,且∠ADC =∠AEB.
学科网(北京)股份有限公司(1)求证:BE是 O的切线;
(2)当 O的半径为2,BC =3时,求tan∠AEB的值.
21.(10分)在平面直角坐标系xOy中,点P ( 2,−3 )在二次函数y =ax2 +bx−3 ( a>0 )的图象上,记该二次
函数图象的对称轴为直线x=m.
(1)求m的值;
(2)若点Q ( m,−4 )在y =ax2 +bx−3的图象上,将该二次函数的图象向上平移5个单位长度,得到新的二
次函数的图象.当0≤ x≤4时,求新的二次函数的最大值与最小值的和;
(3)设y =ax2 +bx−3的图象与x轴交点为( x ,0 ) , ( x ,0 )( x < x ).若4< x −x <6,求a的取值范围.
1 2 1 2 2 1
22.(10分)如图,在Rt△ABC中,点D是斜边AB上的动点(点D与点A不重合),连接CD,以CD为直
CE CB
角边在CD的右侧构造Rt△CDE,∠DCE =90°,连接BE, = =m.
CD CA
图1 图2 图3
(1)如图1,当m=1时,BE与AD之间的位置关系是__________,数量关系是__________.
(2)如图2,当m≠1时,猜想BE与AD之间的位置关系和数量关系,并证明猜想.
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF ,如图3.已知AC =6,设AD= x,四
边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF =2时,请直接写出AD的长度.
学科网(北京)股份有限公司