文档内容
2024—2025 学年度第一学期开学考试
数学试题
第八届贯通实验班数学组
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
一、单选题(本大题有 8个小题,每小题 5分,共 40分)
M ={ x∣−1≤ x≤3 } N = { x∣x=2k−1,k∈N* }
1. 集合 和 关系的Venn图如图所示,则阴影部分表示的集
合中的元素有( )
A. −1 B. 0 C. 1 D. 5
2. 命题“∃x∈R,x2 +lnx>0”的否定是( )
A. ∃x∈R,x2 +lnx≥0 B. ∃x∈R,x2 +lnx<0
C. ∀x∈R,x2 +lnx≥0 D. ∀x∈R,x2 +lnx≤0
3. “不积跬步,无以至千里,不积小流,无以成江海.”此句话是出自荷子的《劝学》,由此推断,其中最后
一句“积小流”是“成江海”的( )
A. 充分条件 B. 必要条件
C. 充要条件 D. 既不充分也不必要条件
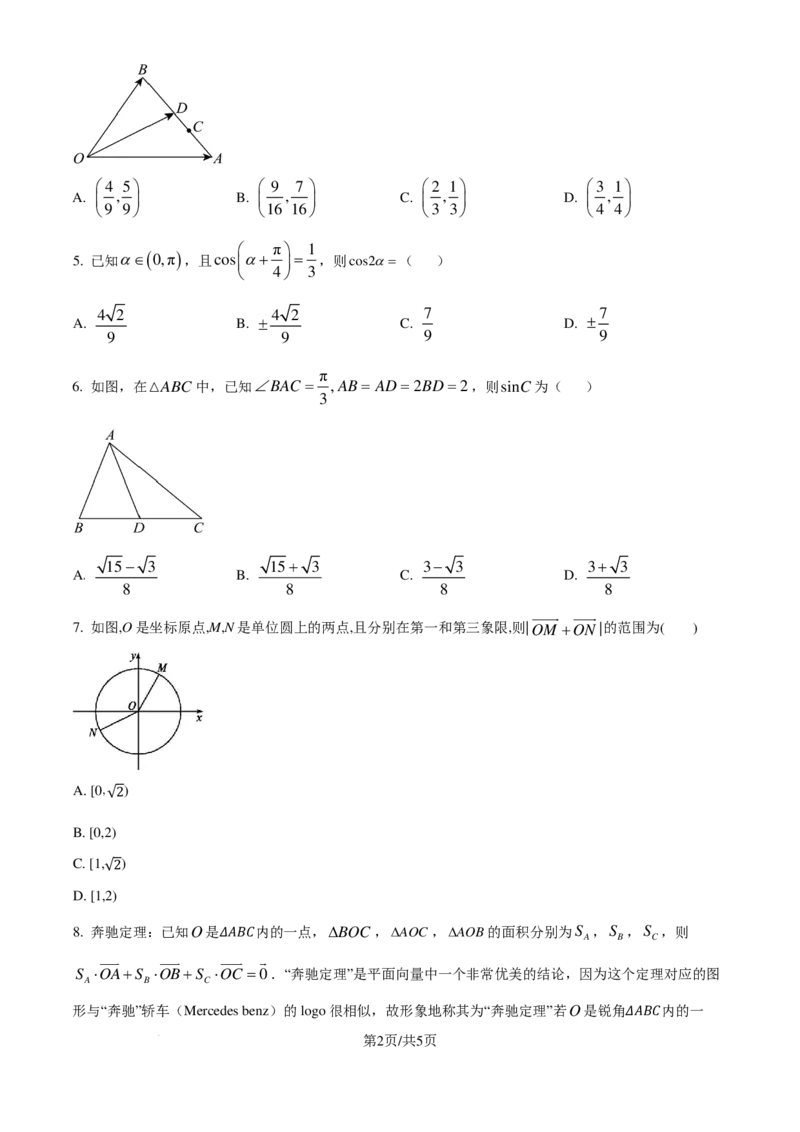
4. 已知OA=a,OB=b,C为线段AB上距A较近的一个三等分点,D为线段CB上距C较近的一个三
{ }
等分点,则OD在基 a,b 下的坐标为( )
第1页/共5页
学科网(北京)股份有限公司4 5 9 7 2 1 3 1
A. , B. , C. , D. ,
9 9 16 16 3 3 4 4
π 1
5. 已知α∈( 0,π ) ,且cos α+ = ,则cos2α=( )
4 3
4 2 4 2 7 7
A. B. ± C. D. ±
9 9 9 9
π
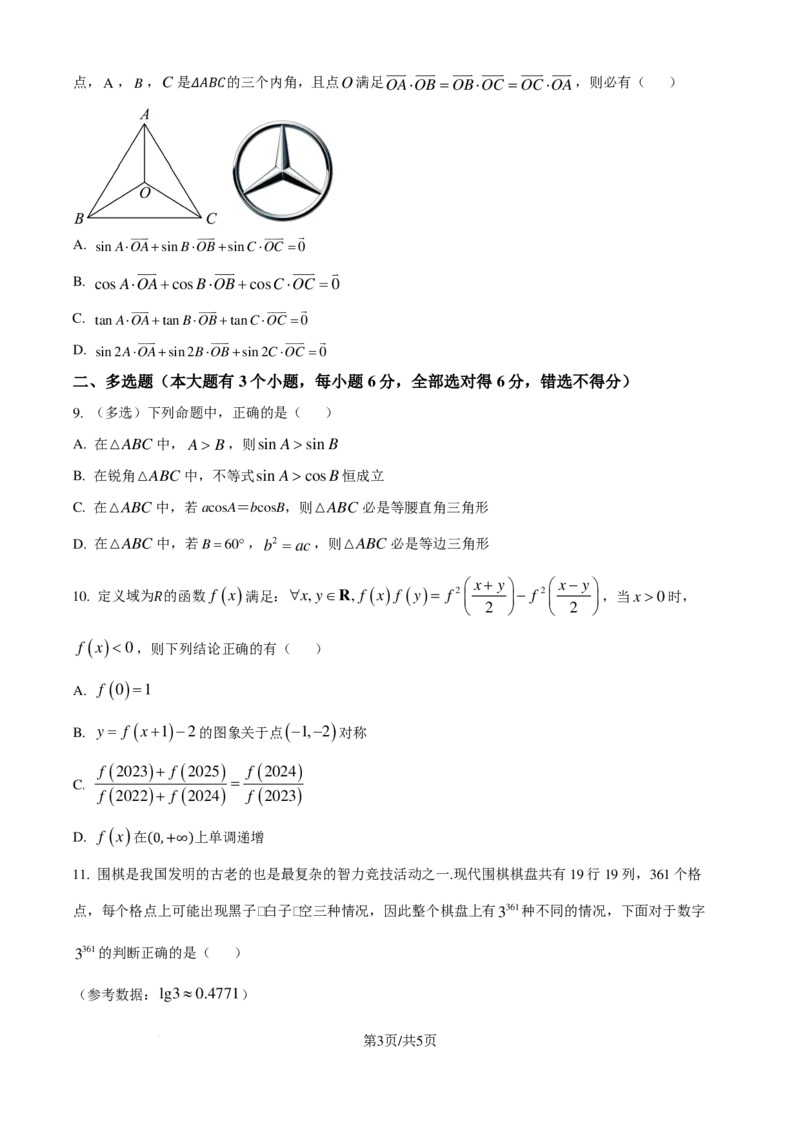
6. 如图,在ABC中,已知∠BAC = ,AB= AD=2BD=2,则sinC为( )
3
15− 3 15+ 3 3− 3 3+ 3
A. B. C. D.
8 8 8 8
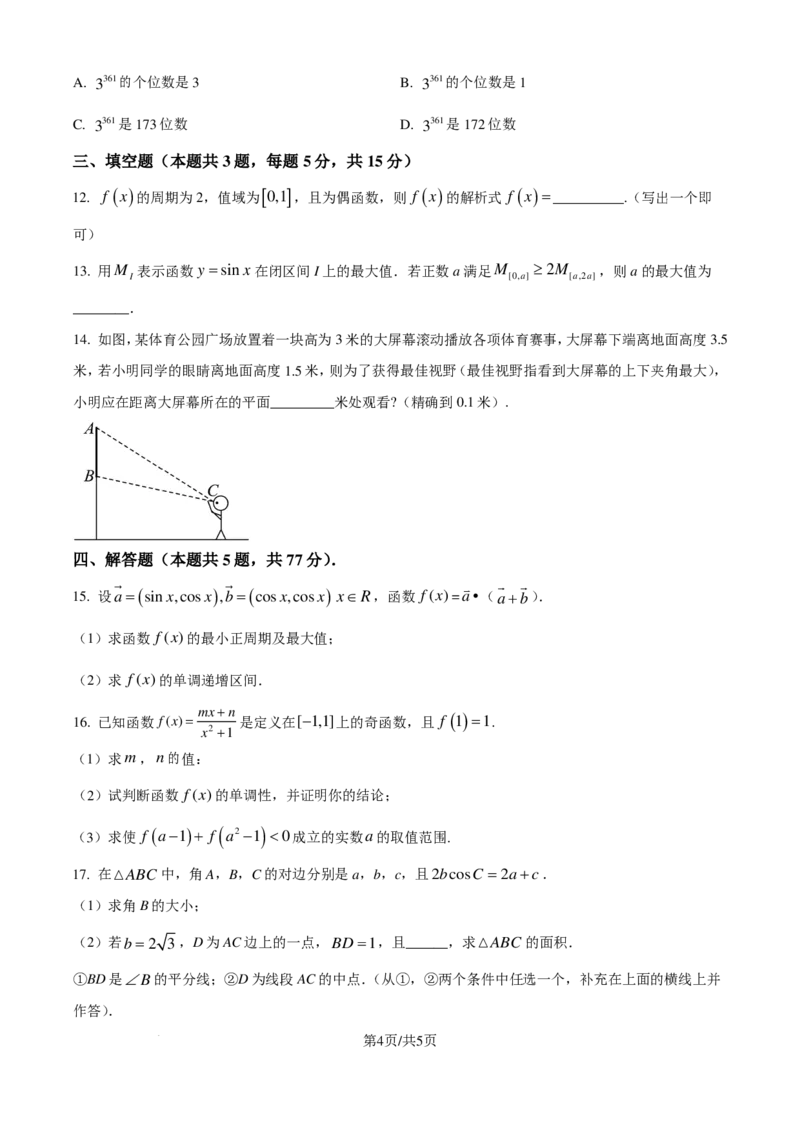
7. 如图,O是坐标原点,M,N是单位圆上的两点,且分别在第一和第三象限,则|OM +ON|的范围为( )
A. [0, )
√2
B. [0,2)
C. [1, )
D. [1,√2)2
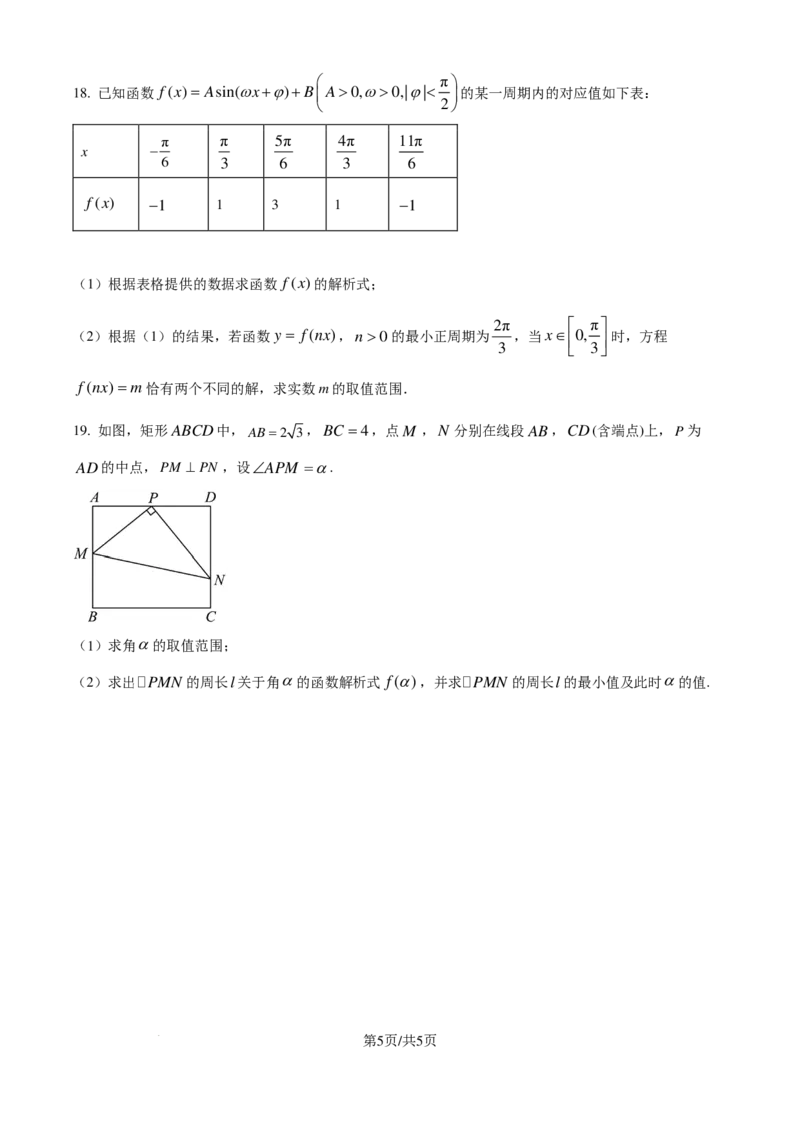
8. 奔驰定理:已知O是 内的一点,∆BOC,∆AOC,∆AOB的面积分别为S ,S ,S ,则
A B C
𝛥𝛥𝛥𝛥𝛥𝛥𝛥𝛥
S ⋅OA+S ⋅OB+S ⋅OC =0.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图
A B C
形与“奔驰”轿车(Mercedes benz)的logo很相似,故形象地称其为“奔驰定理”若O是锐角 内的一
第2页/共5页 𝛥𝛥𝛥𝛥𝛥𝛥𝛥𝛥
学科网(北京)股份有限公司
点,A,B,C是 的三个内角,且点O满足OA⋅OB=OB⋅OC =OC⋅OA,则必有( )
𝛥𝛥𝛥𝛥𝛥𝛥𝛥𝛥
A. sinA⋅OA+sinB⋅OB+sinC⋅OC =0
B. cosA⋅OA+cosB⋅OB+cosC⋅OC =0
C. tanA⋅OA+tanB⋅OB+tanC⋅OC =0
D. sin2A⋅OA+sin2B⋅OB+sin2C⋅OC =0
二、多选题(本大题有 3个小题,每小题 6分,全部选对得 6分,错选不得分)
9. (多选)下列命题中,正确的是( )
A. 在ABC中,A> B,则sinA>sinB
B. 在锐角ABC中,不等式sin A>cosB恒成立
C. 在ABC中,若acosA=bcosB,则ABC必是等腰直角三角形
D. 在ABC中,若B=60°,b2 =ac,则ABC必是等边三角形
x+ y x− y
10. 定义域为 的函数 f ( x ) 满足:∀x,y∈R, f ( x ) f ( y )= f 2 − f 2 ,当x>0时,
2 2
𝑅𝑅
f
(
x
)<0,则下列结论正确的有(
)
A. f
(
0
)=1
B. y = f ( x+1 )−2的图象关于点 (−1,−2 ) 对称
f
(
2023
)+
f
(
2025
)
f
(
2024
)
C. =
f
(
2022
)+
f
(
2024
)
f
(
2023
)
( )
D. f x 在 上单调递增
11. 围棋是我
(0国,+发∞明 )
的古老的也是最复杂的智力竞技活动之一.现代围棋棋盘共有19行19列,361个格
点,每个格点上可能出现黑子、白子、空三种情况,因此整个棋盘上有3361种不同的情况,下面对于数字
3361的判断正确的是( )
(参考数据:lg3≈0.4771)
第3页/共5页
学科网(北京)股份有限公司A. 3361的个位数是3 B. 3361的个位数是1
C. 3361是173位数 D. 3361是172位数
三、填空题(本题共 3题,每题 5分,共 15分)
12. f
(
x
)
的周期为2,值域为
[
0,1
]
,且为偶函数,则 f
(
x
)
的解析式 f
(
x
)=__________.(写出一个即
可)
13. 用M 表示函数y =sinx在闭区间I上的最大值.若正数a满足M ≥2M ,则a的最大值为
I [0,a] [a,2a]
________.
14. 如图,某体育公园广场放置着一块高为3米的大屏幕滚动播放各项体育赛事,大屏幕下端离地面高度3.5
米,若小明同学的眼睛离地面高度1.5米,则为了获得最佳视野(最佳视野指看到大屏幕的上下夹角最大),
小明应在距离大屏幕所在的平面_________米处观看?(精确到0.1米).
四、解答题(本题共 5题,共 77分).
15. 设a=( sinx,cosx ) ,b=( cosx,cosx ) x∈R,函数 f(x)=a•(a+b).
(1)求函数 f(x)的最小正周期及最大值;
(2)求 f(x)的单调递增区间.
16. 已知函数 f(x)=
mx+n
是定义在[−1,1]上的奇函数,且 f ( 1 )=1.
x2 +1
(1)求m,n的值:
(2)试判断函数 f(x)的单调性,并证明你的结论;
(3)求使 f ( a−1 )+ f ( a2 −1 ) <0成立的实数a的取值范围.
17. 在ABC中,角A,B,C的对边分别是a,b,c,且2bcosC =2a+c.
(1)求角B的大小;
(2)若b=2 3,D为AC边上的一点,BD=1,且______,求ABC的面积.
①BD是∠B的平分线;②D为线段AC的中点.(从①,②两个条件中任选一个,补充在上面的横线上并
作答).
第4页/共5页
学科网(北京)股份有限公司 π
18. 已知函数 f(x)= Asin(ωx+ϕ)+BA>0,ω>0,|ϕ|< 的某一周期内的对应值如下表:
2
π π 5π 4π 11π
x −
6 3 6 3 6
f(x) −1 1 3 1 −1
(1)根据表格提供的数据求函数 f(x)的解析式;
2π π
(2)根据(1)的结果,若函数y = f(nx),n>0的最小正周期为 ,当x∈
0,
时,方程
3 3
f(nx)=m恰有两个不同的解,求实数m的取值范围.
19. 如图,矩形ABCD中,AB=2 3,BC =4,点M ,N 分别在线段AB,CD(含端点)上,P为
AD的中点,PM ⊥PN ,设∠APM =α.
(1)求角α的取值范围;
(2)求出PMN 的周长l关于角α的函数解析式 f(α),并求PMN 的周长l的最小值及此时α的值.
第5页/共5页
学科网(北京)股份有限公司