文档内容
2024-2025 学年度春学期期中联考试卷
高一数学
命题人:徐波 复核人:高强
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求
的。
1.已知点 ,向量 ,则向量 =( )
A. B. C. D.
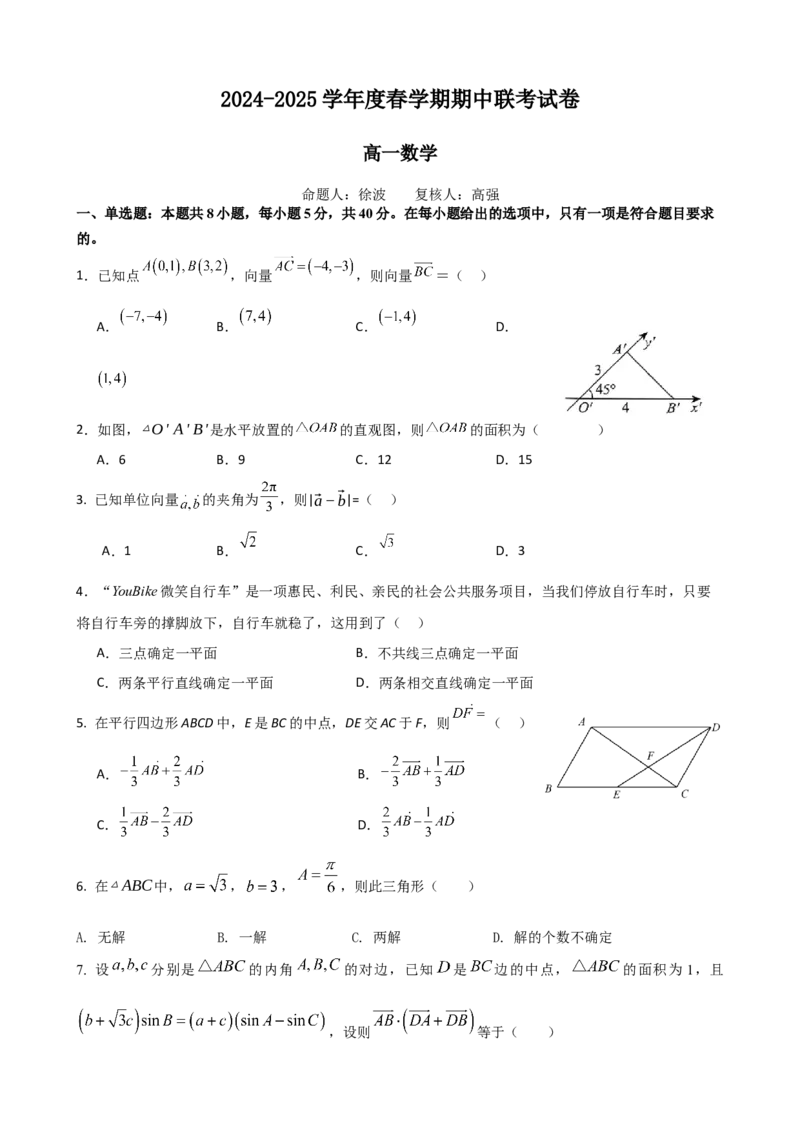
2.如图,△O' A'B'是水平放置的 的直观图,则 的面积为( )
A.6 B.9 C.12 D.15
3. 已知单位向量 的夹角为 ,则|⃗a−⃗b|=( )
A.1 B. C. D.3
4.“YouBike微笑自行车”是一项惠民、利民、亲民的社会公共服务项目,当我们停放自行车时,只要
将自行车旁的撑脚放下,自行车就稳了,这用到了( )
A.三点确定一平面 B.不共线三点确定一平面
C.两条平行直线确定一平面 D.两条相交直线确定一平面
5. 在平行四边形ABCD中,E是BC的中点,DE交AC于F,则 ( )
A. B.
C. D.
6. 在△ABC中, , , ,则此三角形( )
A. 无解 B. 一解 C. 两解 D. 解的个数不确定
7. 设 分别是 的内角 的对边,已知 是 边的中点, 的面积为1,且
,设则 等于( )A. B. C. D.2
8.设直三棱柱 的所有顶点都在一个表面积是 的球面上,且 ,
则该直三棱柱的体积是( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共计18分.在每小题给出的四个选项中,有多项符合题目
要求.全部选对得6分,部分选对得部分分,有选错的得0分.
9.已知复数 ,则( )
A. 的虚部为 B.
C. 在复平面内的对应点位于直线 上 D. 为方程 的一个根
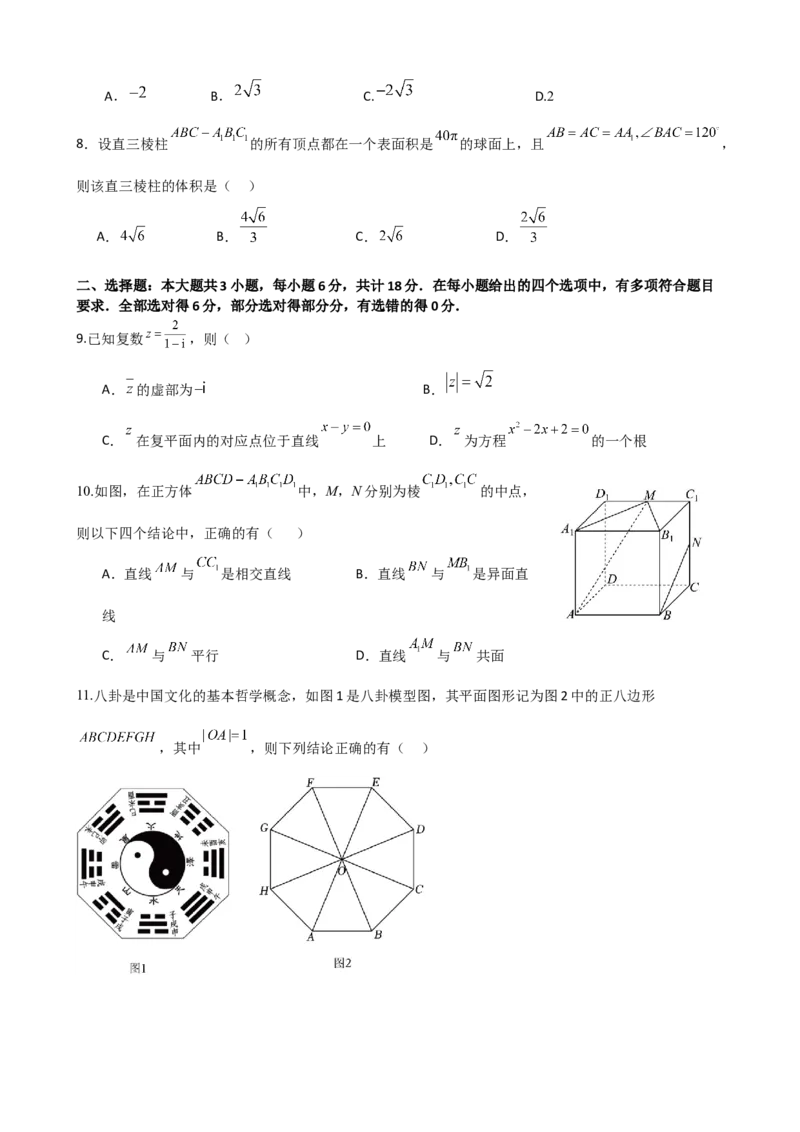
10.如图,在正方体 中,M,N分别为棱 的中点,
则以下四个结论中,正确的有( )
A.直线 与 是相交直线 B.直线 与 是异面直
线
C. 与 平行 D.直线 与 共面
11.八卦是中国文化的基本哲学概念,如图1是八卦模型图,其平面图形记为图2中的正八边形
,其中 ,则下列结论正确的有( )A. B.
C. D. 在 向量上的投影向量为
三、填空题:本大题共3小题,每小题5分,共计15分.
12.已知平面向量 , 不共线,且 , , ,若 , , 三点共
线,则 .
13.某校研究性学习小组想要测量某塔的高度,现选取与塔底 在同一个水平面内的两个测量基点A与
,现测得 , , 米,在点A处测得塔顶 的仰角为 ,则塔高 为
米.
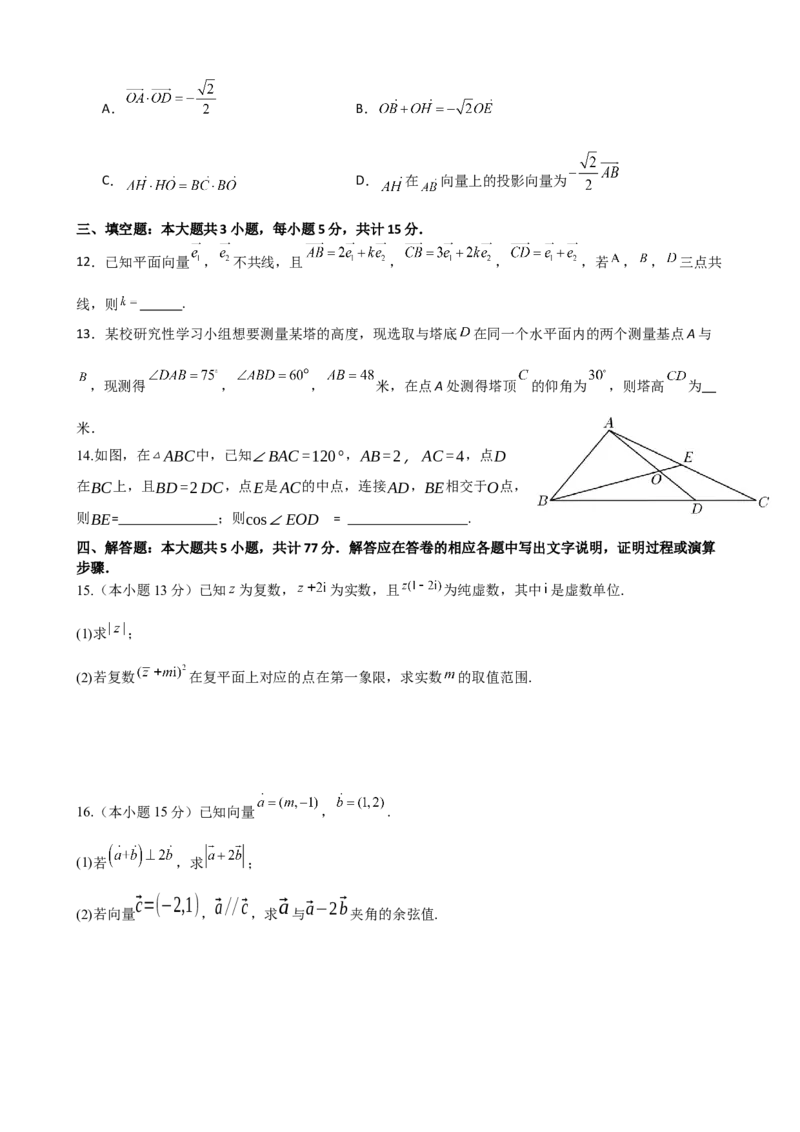
14.如图,在△ABC中,已知∠BAC=120°,AB=2,AC=4,点D
在BC上,且BD=2DC,点E是AC的中点,连接AD,BE相交于O点,
则BE= ;则cos∠EOD = .
四、解答题:本大题共5小题,共计77分.解答应在答卷的相应各题中写出文字说明,证明过程或演算
步骤.
15.(本小题13分)已知 为复数, 为实数,且 为纯虚数,其中 是虚数单位.
(1)求 ;
(2)若复数 在复平面上对应的点在第一象限,求实数 的取值范围.
16.(本小题15分)已知向量 , .
(1)若 ,求 ;
⃗c=(−2,1) ⃗a//⃗c ⃗a ⃗a−2⃗b
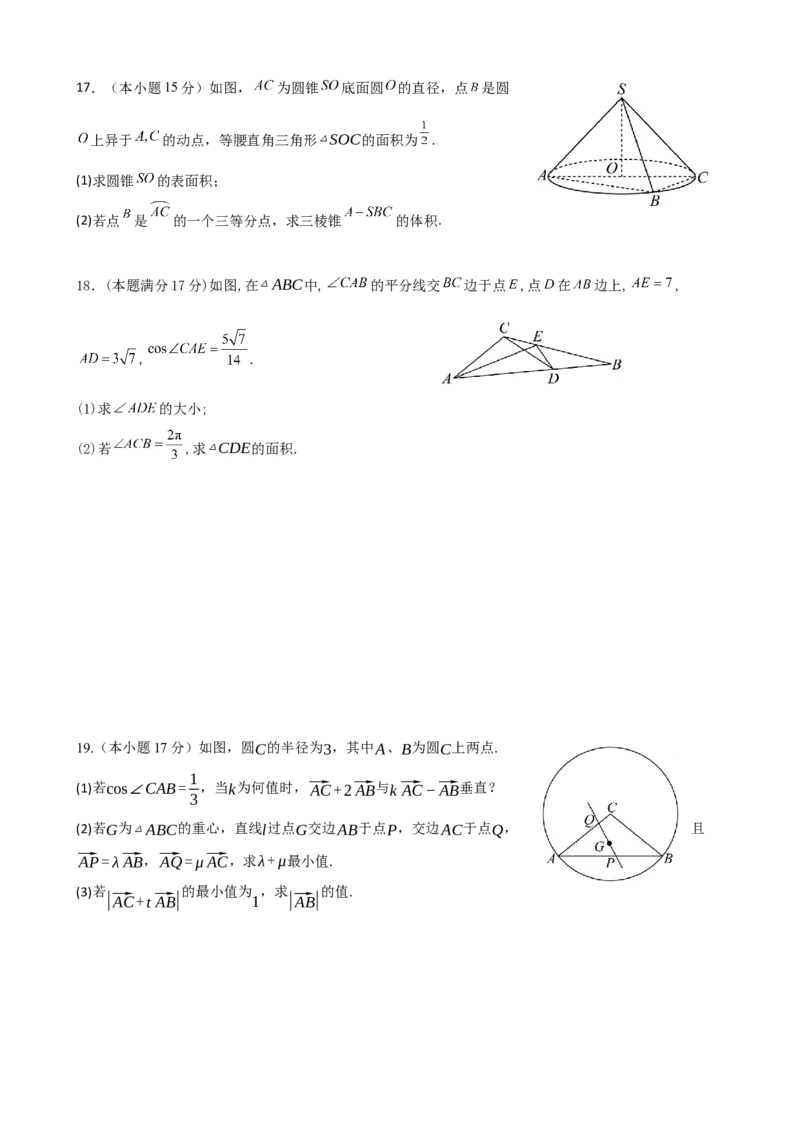
(2)若向量 , ,求 与 夹角的余弦值.17.(本小题15分)如图, 为圆锥 底面圆 的直径,点 是圆
上异于 的动点,等腰直角三角形△SOC的面积为 .
(1)求圆锥 的表面积;
(2)若点 是 的一个三等分点,求三棱锥 的体积.
18.(本题满分17分)如图,在△ABC中, 的平分线交 边于点 ,点 在 边上, ,
, .
(1)求 的大小;
(2)若 ,求△CDE的面积.
19.(本小题17分)如图,圆C的半径为3,其中A、B为圆C上两点.
1
(1)若cos∠CAB= ,当k为何值时,⃗AC+2⃗AB与k⃗AC−⃗AB垂直?
3
(2)若G为△ABC的重心,直线l过点G交边AB于点P,交边AC于点Q, 且
⃗AP=λ⃗AB,⃗AQ=μ⃗AC,求λ+μ最小值.
(3)若 的最小值为 ,求 的值.
|⃗AC+t⃗AB| 1 |⃗AB|2024-2025 学年度春学期期中联考试卷
高一数学答案
二、单选题:
1-4.A C C B 5-8. D C B A
二、选择题:
9.BCD 10.BD 11.ABD
三、填空题:
3√39
12. 1 13. 14. 2√3 ,
26
五、解答题:
15.(1)设z=a+bi,a,b∈R,z+2i=a+(b+2)i,
因为z+2i为实数,所以b+2=0,即b=−2 ............................................................................(2分)
所以z(1−2i)=(a−2i)(1−2i)=a−4−2(a+1)i,
又因为z(1−2i)为纯虚数, 所以a−4=0即a=4,所以z=4−2i,..................................(4分)
所以 ........................................................................................................(6分)
|z|=√42+(−2) 2=2√5
(2)由(1)知, z=4+2i,
所以 ,................................................(9分)
(z+mi) 2=(4+2i+mi) 2=16−(m+2) 2+8(m+2)i
又因为 在复平面上所对应的点在第一象限,
(z+mi) 2
所以¿ ,...........................................................................................................(11分)
解得:−20
,
μ>0
,则
λ+μ=
1
(λ+μ)
(1
+
1)
=
1(
2+
μ
+
λ)
≥
1(
2+2
√μ
⋅
λ)
=
4,
3 λ μ 3 λ μ 3 λ μ 3
2 4
当且仅当¿时,即当λ=μ= 时,λ+μ取最小值 ................................................(11分)
3 3
(3)设AB=m(m>0),取线段AB的中点E,连接CE,则CE⊥AB,1 2
则⃗AC⋅⃗AB=(⃗AE+⃗EC)⋅⃗AB=⃗AE⋅⃗AB+⃗EC⋅⃗AB= |⃗AB|,
2
又
|⃗AC+t⃗AB|=√(⃗AC+t⃗AB) 2 =√⃗AC2+2t⃗AB⋅⃗AC+t2⃗AB2=√9+t⃗AB2+t2⃗AB2
=√9+m2t+t2m2= √ m2( t+ 1) 2 +9− m2,...........................................................................(14分)
2 4
所以当 1时, 有最小值√ m2,所以√ m2 ,解得 ,
t=− |⃗AC+t⃗AB| 9− 9− =1 m=4√2
2 4 4
即 取最小值 时, ..............................................................................(17分)
|⃗AC+t⃗AB| 1 |⃗AB|=4√2