文档内容
第八章 立体几何初步A(基础卷)
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
第Ⅰ卷(选择题)
请点击修改第I卷的文字说明
评卷人 得 分
一.选择题(共8小题)
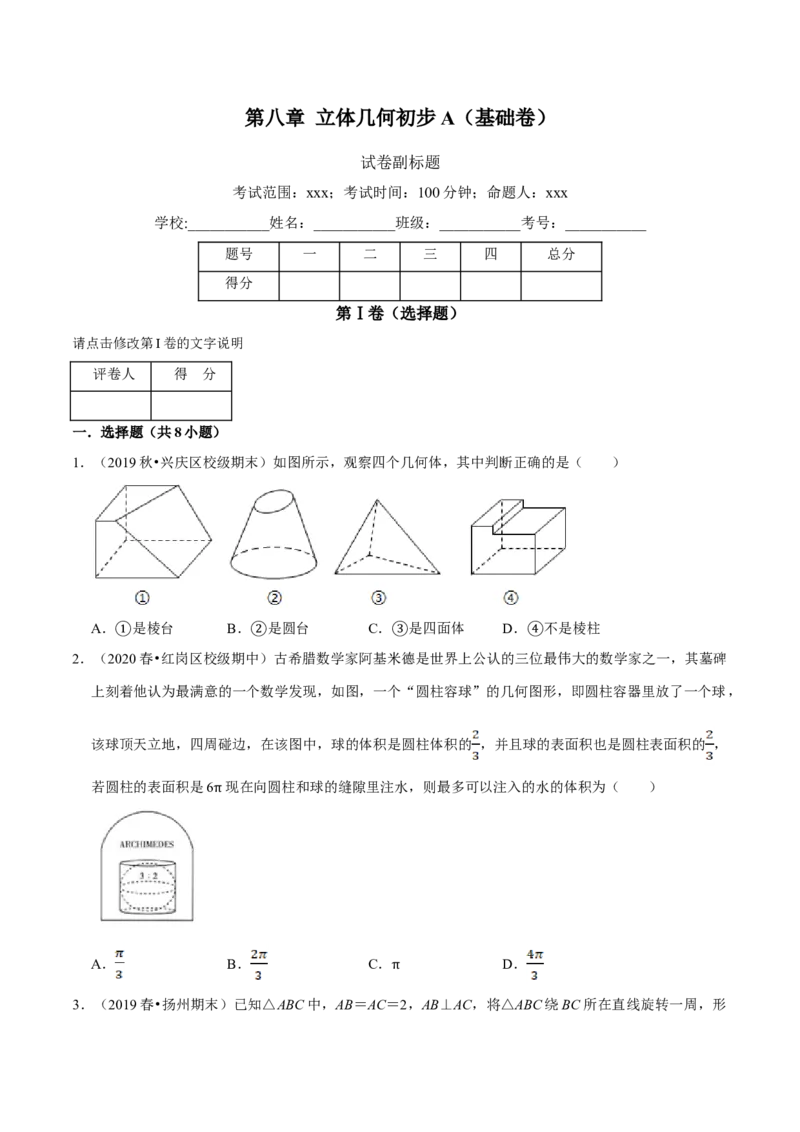
1.(2019秋•兴庆区校级期末)如图所示,观察四个几何体,其中判断正确的是( )
A. 是棱台 B. 是圆台 C. 是四面体 D. 不是棱柱
2.(20①20春•红岗区校级期中②)古希腊数学家阿基米③德是世界上公认的三④位最伟大的数学家之一,其墓碑
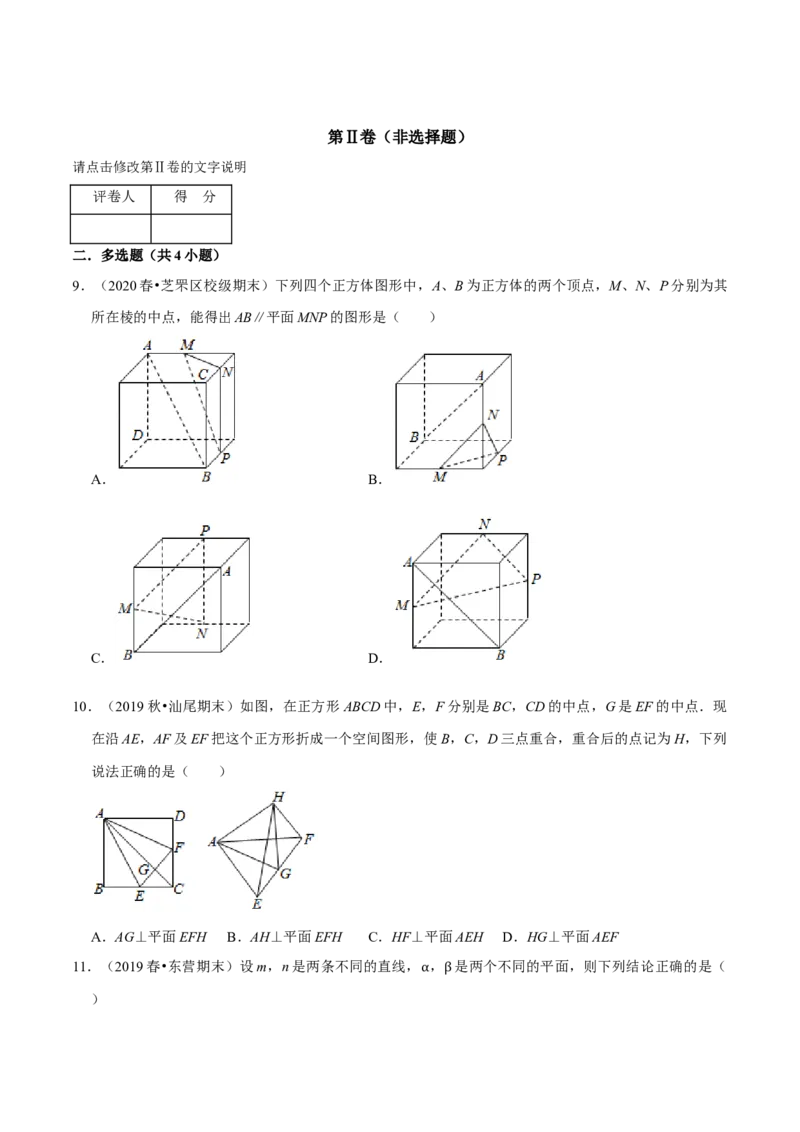
上刻着他认为最满意的一个数学发现,如图,一个“圆柱容球”的几何图形,即圆柱容器里放了一个球,
该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的 ,并且球的表面积也是圆柱表面积的 ,
若圆柱的表面积是6 现在向圆柱和球的缝隙里注水,则最多可以注入的水的体积为( )
π
A. B. C. D.
π
3.(2019春•扬州期末)已知△ABC中,AB=AC=2,AB⊥AC,将△ABC绕BC所在直线旋转一周,形成几何体K,则几何体K的表面积为( )
A. B. C. D.
4.(2019春•湖南期末)已知 、 为两个不同平面,l为直线且l⊥ ,则“ ⊥ ”是“l∥ ”( )
A.充分不必要条件 α β B.必要不充分条件β α β α
C.充要条件 D.既不充分也不必要条件
5.(2020春•顺德区月考)已知正三棱柱ABC﹣A B C ,O为△ABC的外心,则异面直线AC 与OB所成
1 1 1 1
角的大小为( )
A.30° B.60° C.45° D.90°
6.(2019秋•安庆期末)下列命题的符号语言中,不是公理的是( )
A.a⊥ ,b⊥ a∥b
B.P α,且Pα⇒ ∩ =l,且P l
C.A∈αl,B l,∈且β⇒Aα ,βB l ∈
D.a∥∈ b,a∈∥c b∥∈cα ∈α⇒⊂α
7.(2019秋•滑县⇒期末)在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点
M在线段PC上,PM=tPC,PA∥平面MQB,则实数t的值为( )
A. B. C. D.
8.(2020•聊城模拟)我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童
ABCD﹣EFGH有外接球,且AB=2 ,平面ABCD与平面EFGH
间的距离为1,则该刍童外接球的体积为( )
A.12 B.24 C.36 D.48
π π π π第Ⅱ卷(非选择题)
请点击修改第Ⅱ卷的文字说明
评卷人 得 分
二.多选题(共4小题)
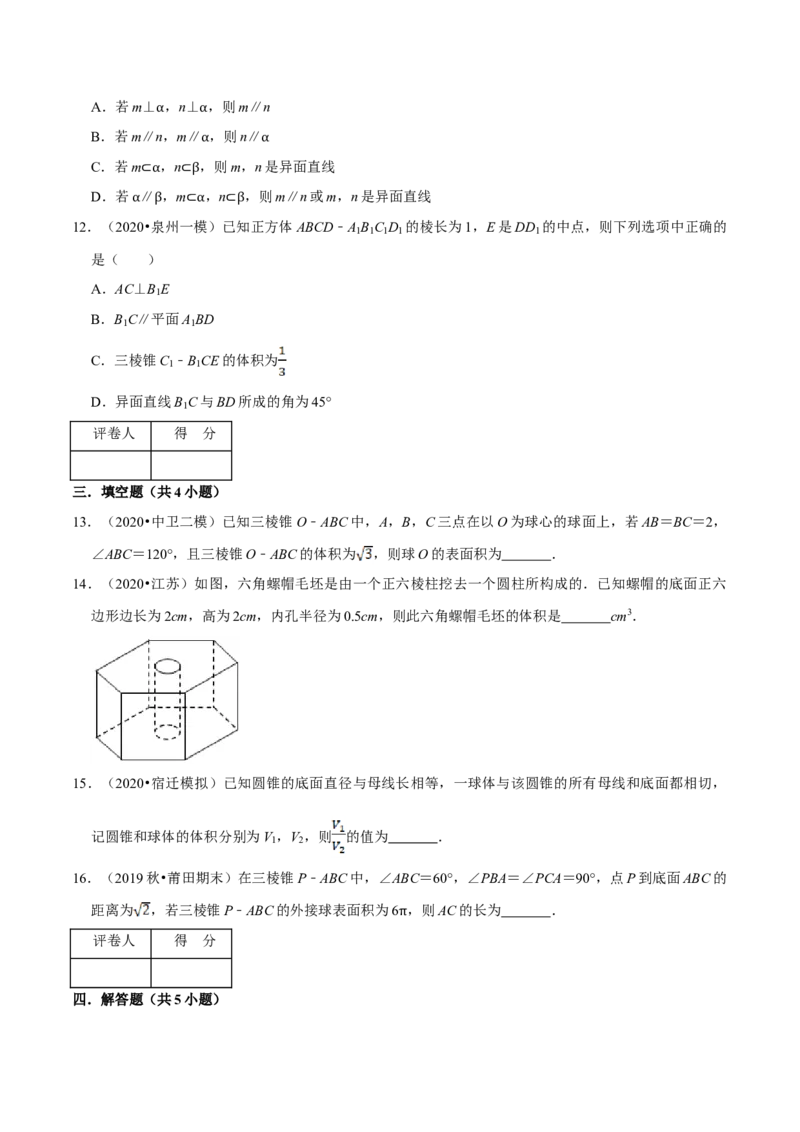
9.(2020春•芝罘区校级期末)下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其
所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B.
C. D.
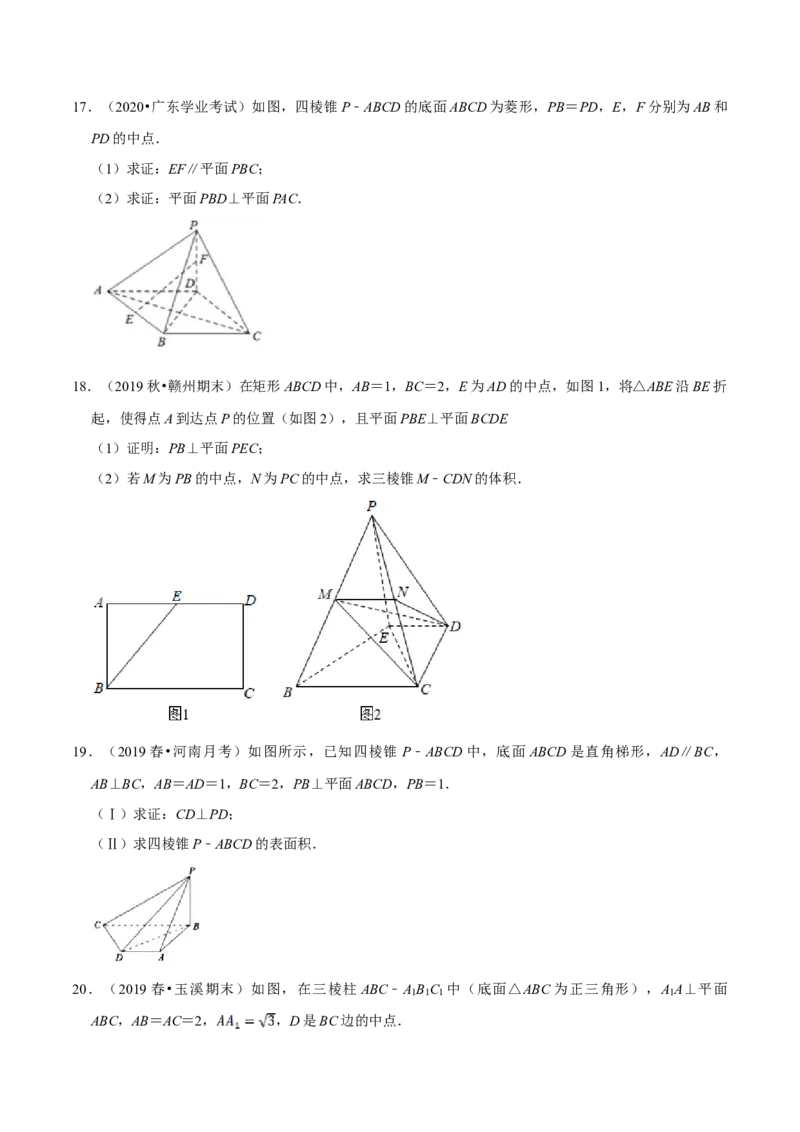
10.(2019秋•汕尾期末)如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现
在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列
说法正确的是( )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
11.(2019春•东营期末)设m,n是两条不同的直线, , 是两个不同的平面,则下列结论正确的是(
) α βA.若m⊥ ,n⊥ ,则m∥n
B.若m∥nα,m∥α,则n∥
C.若m ,n ,α 则m,nα是异面直线
D.若 ∥⊂α,m⊂β ,n ,则m∥n或m,n是异面直线
12.(202α0•泉β州一⊂模α)已⊂知β 正方体ABCD﹣A
1
B
1
C
1
D
1
的棱长为1,E是DD
1
的中点,则下列选项中正确的
是( )
A.AC⊥B E
1
B.B C∥平面A BD
1 1
C.三棱锥C ﹣B CE的体积为
1 1
D.异面直线B C与BD所成的角为45°
1
评卷人 得 分
三.填空题(共4小题)
13.(2020•中卫二模)已知三棱锥O﹣ABC中,A,B,C三点在以O为球心的球面上,若AB=BC=2,
∠ABC=120°,且三棱锥O﹣ABC的体积为 ,则球O的表面积为 .
14.(2020•江苏)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六
边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是 cm3.
15.(2020•宿迁模拟)已知圆锥的底面直径与母线长相等,一球体与该圆锥的所有母线和底面都相切,
记圆锥和球体的体积分别为V ,V ,则 的值为 .
1 2
16.(2019秋•莆田期末)在三棱锥P﹣ABC中,∠ABC=60°,∠PBA=∠PCA=90°,点P到底面ABC的
距离为 ,若三棱锥P﹣ABC的外接球表面积为6 ,则AC的长为 .
评卷人 得 分 π
四.解答题(共5小题)17.(2020•广东学业考试)如图,四棱锥P﹣ABCD的底面ABCD为菱形,PB=PD,E,F分别为AB和
PD的中点.
(1)求证:EF∥平面PBC;
(2)求证:平面PBD⊥平面PAC.
18.(2019秋•赣州期末)在矩形ABCD中,AB=1,BC=2,E为AD的中点,如图1,将△ABE沿BE折
起,使得点A到达点P的位置(如图2),且平面PBE⊥平面BCDE
(1)证明:PB⊥平面PEC;
(2)若M为PB的中点,N为PC的中点,求三棱锥M﹣CDN的体积.
19.(2019春•河南月考)如图所示,已知四棱锥 P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,
AB⊥BC,AB=AD=1,BC=2,PB⊥平面ABCD,PB=1.
(Ⅰ)求证:CD⊥PD;
(Ⅱ)求四棱锥P﹣ABCD的表面积.
20.(2019春•玉溪期末)如图,在三棱柱 ABC﹣A B C 中(底面△ABC为正三角形),A A⊥平面
1 1 1 1
ABC,AB=AC=2, ,D是BC边的中点.(1)证明:平面ADB ⊥平面BB C C.
1 1 1
(2)求点B到平面ADB 的距离.
1
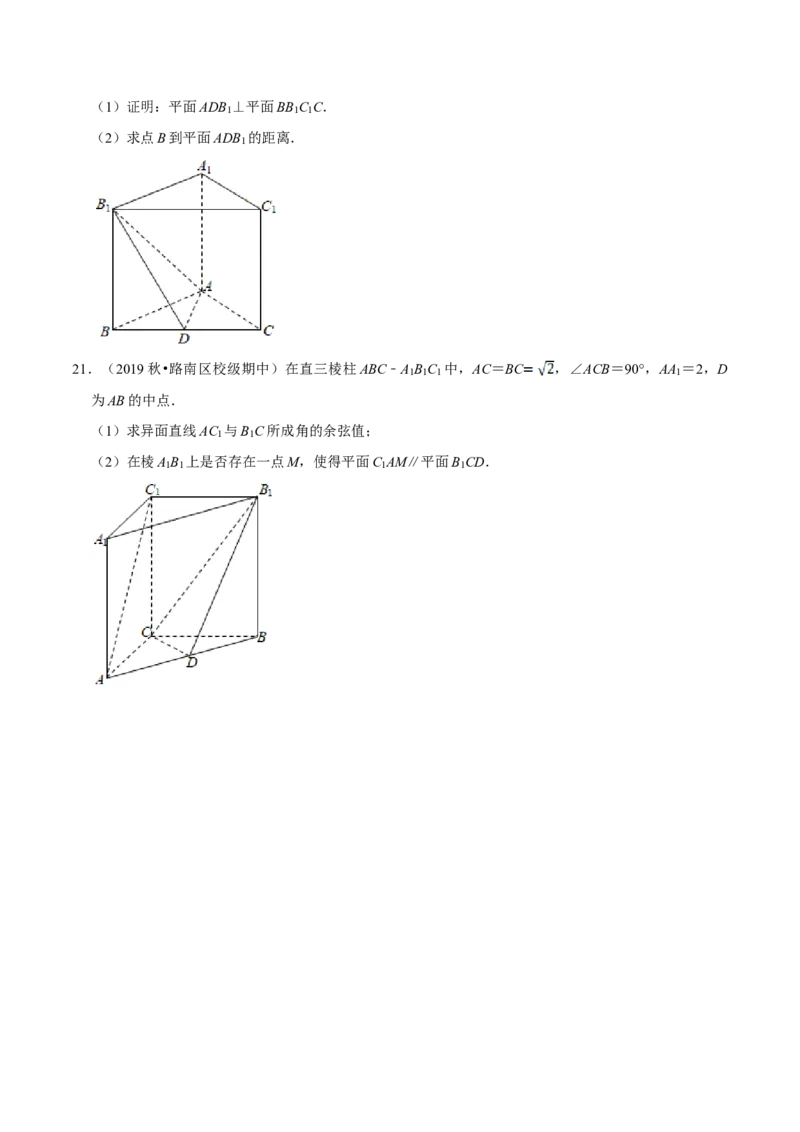
21.(2019秋•路南区校级期中)在直三棱柱ABC﹣A B C 中,AC=BC ,∠ACB=90°,AA =2,D
1 1 1 1
为AB的中点.
(1)求异面直线AC 与B C所成角的余弦值;
1 1
(2)在棱A B 上是否存在一点M,使得平面C AM∥平面B CD.
1 1 1 1