文档内容
第八章 立体几何初步A(基础卷)
参考答案与试题解析
一.选择题(共8小题)
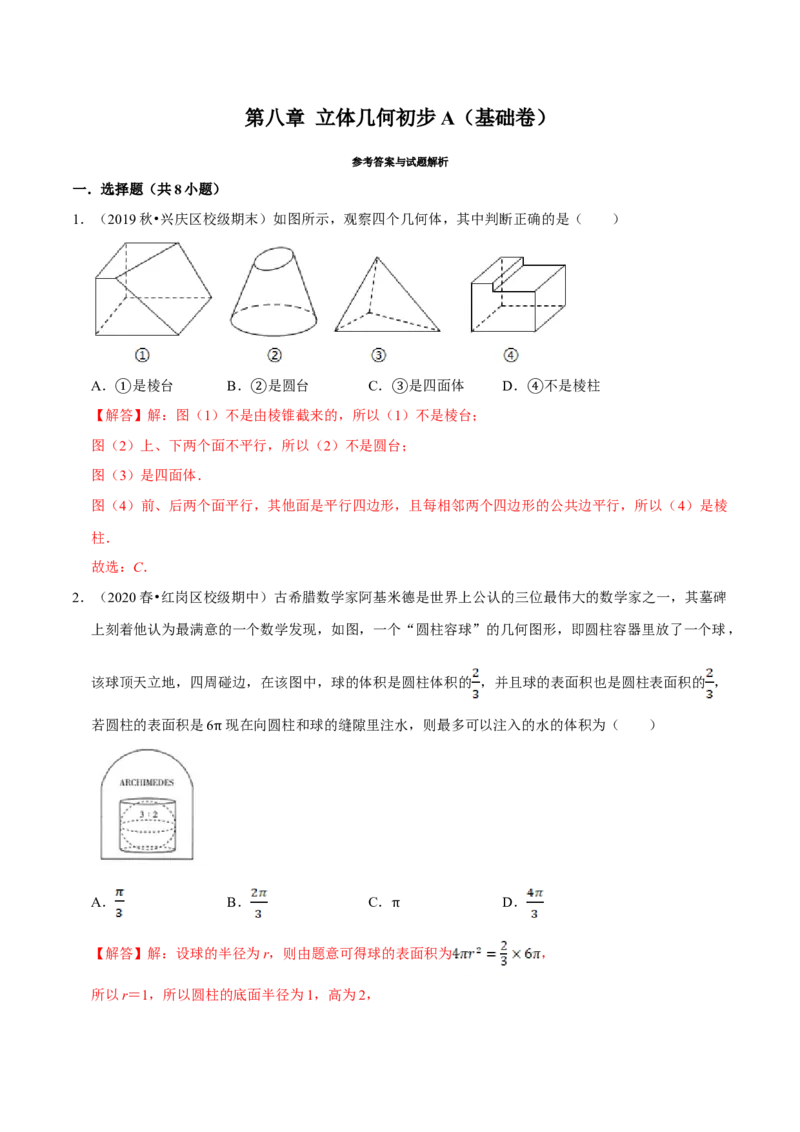
1.(2019秋•兴庆区校级期末)如图所示,观察四个几何体,其中判断正确的是( )
A. 是棱台 B. 是圆台 C. 是四面体 D. 不是棱柱
【解①答】解:图(1)不是②由棱锥截来的,所以(③1)不是棱台; ④
图(2)上、下两个面不平行,所以(2)不是圆台;
图(3)是四面体.
图(4)前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以(4)是棱
柱.
故选:C.
2.(2020春•红岗区校级期中)古希腊数学家阿基米德是世界上公认的三位最伟大的数学家之一,其墓碑
上刻着他认为最满意的一个数学发现,如图,一个“圆柱容球”的几何图形,即圆柱容器里放了一个球,
该球顶天立地,四周碰边,在该图中,球的体积是圆柱体积的 ,并且球的表面积也是圆柱表面积的 ,
若圆柱的表面积是6 现在向圆柱和球的缝隙里注水,则最多可以注入的水的体积为( )
π
A. B. C. D.
π
【解答】解:设球的半径为r,则由题意可得球的表面积为 ,
所以r=1,所以圆柱的底面半径为1,高为2,所以最多可以注入的水的体积为 .
故选:B.
3.(2019春•扬州期末)已知△ABC中,AB=AC=2,AB⊥AC,将△ABC绕BC所在直线旋转一周,形
成几何体K,则几何体K的表面积为( )
A. B. C. D.
【解答】解:由题知该几何体为两个倒立的圆锥底对底组合在一起,其中若L=2,R
∴S ×2 2×2=4
π π
故选:B.
4.(2019春•湖南期末)已知 、 为两个不同平面,l为直线且l⊥ ,则“ ⊥ ”是“l∥ ”( )
A.充分不必要条件 α β B.必要不充分条件β α β α
C.充要条件 D.既不充分也不必要条件
【解答】解:根据题意,当“l∥ ”时,必有“ ⊥ ”,
反之,当“ ⊥ ”时,l可能在平α面 内,即“lα∥ β”不一定成立,
则“ ⊥ ”α是“βl∥ ”的必要不充分α条件; α
故选α:Bβ. α
5.(2020春•顺德区月考)已知正三棱柱ABC﹣A B C ,O为△ABC的外心,则异面直线AC 与OB所成
1 1 1 1
角的大小为( )
A.30° B.60° C.45° D.90°
【解答】解:如图,
∵△ABC是等边三角形,且O为△ABC的外心,
∴O是△ABC的垂心,
∴BO⊥AC,且AA ⊥平面ABC,BO 平面ABC,
1
∴BO⊥AA , ⊂
1
∴BO⊥平面AA C C,且AC 平面AA C C,
1 1 1 1 1
∴BO⊥AC , ⊂
1
∴异面直线AC 与OB所成角的大小为90°.
1
故选:D.6.(2019秋•安庆期末)下列命题的符号语言中,不是公理的是( )
A.a⊥ ,b⊥ a∥b
B.P α,且Pα⇒ ∩ =l,且P l
C.A∈αl,B l,∈且β⇒Aα ,βB l ∈
D.a∥∈ b,a∈∥c b∥∈cα ∈α⇒⊂α
【解答】解:A⇒不是公理,
在B中,由公理三知:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,
故B是公理.
在C中,由公理一知:如果一条直线上的两点在一个平面内,那么这条直线在此平面内,故C是公理;
在D中,由平行公理得:平行于同一条直线的两条直线互相平行,故D是公理;
故选:A.
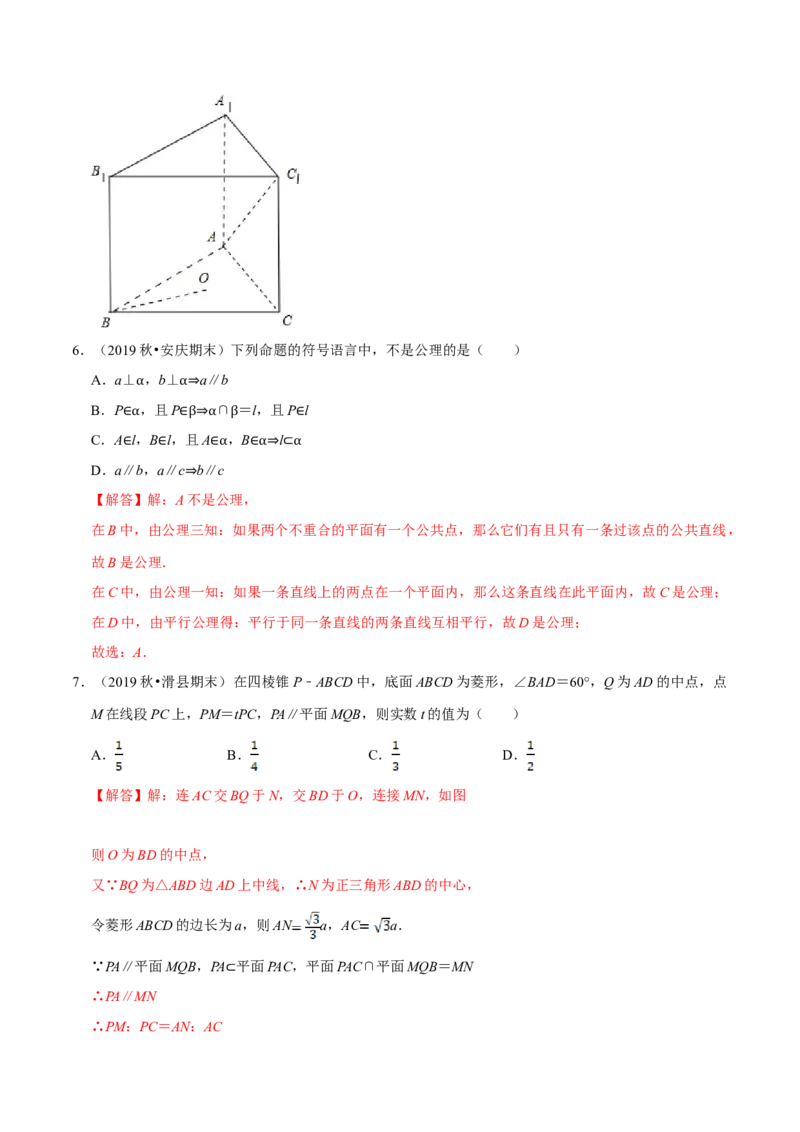
7.(2019秋•滑县期末)在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,点
M在线段PC上,PM=tPC,PA∥平面MQB,则实数t的值为( )
A. B. C. D.
【解答】解:连AC交BQ于N,交BD于O,连接MN,如图
则O为BD的中点,
又∵BQ为△ABD边AD上中线,∴N为正三角形ABD的中心,
令菱形ABCD的边长为a,则AN a,AC a.
∵PA∥平面MQB,PA 平面PAC,平面PAC∩平面MQB=MN
∴PA∥MN ⊂
∴PM:PC=AN:AC即PM PC,t .
故选:C.
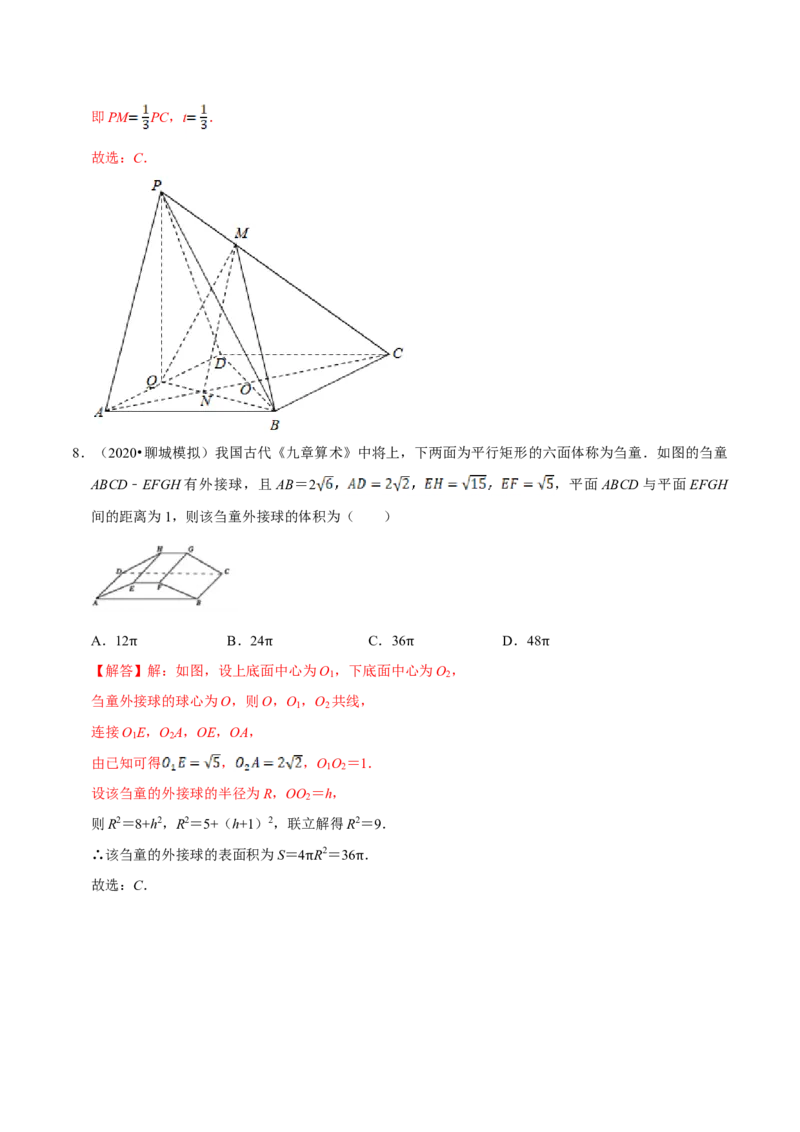
8.(2020•聊城模拟)我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童
ABCD﹣EFGH有外接球,且AB=2 ,平面ABCD与平面EFGH
间的距离为1,则该刍童外接球的体积为( )
A.12 B.24 C.36 D.48
【解答π】解:如图,设上底面π中心为O 1 ,下底面中心π 为O 2 , π
刍童外接球的球心为O,则O,O ,O 共线,
1 2
连接O E,O A,OE,OA,
1 2
由已知可得 , ,O O =1.
1 2
设该刍童的外接球的半径为R,OO =h,
2
则R2=8+h2,R2=5+(h+1)2,联立解得R2=9.
∴该刍童的外接球的表面积为S=4 R2=36 .
故选:C. π π二.多选题(共4小题)
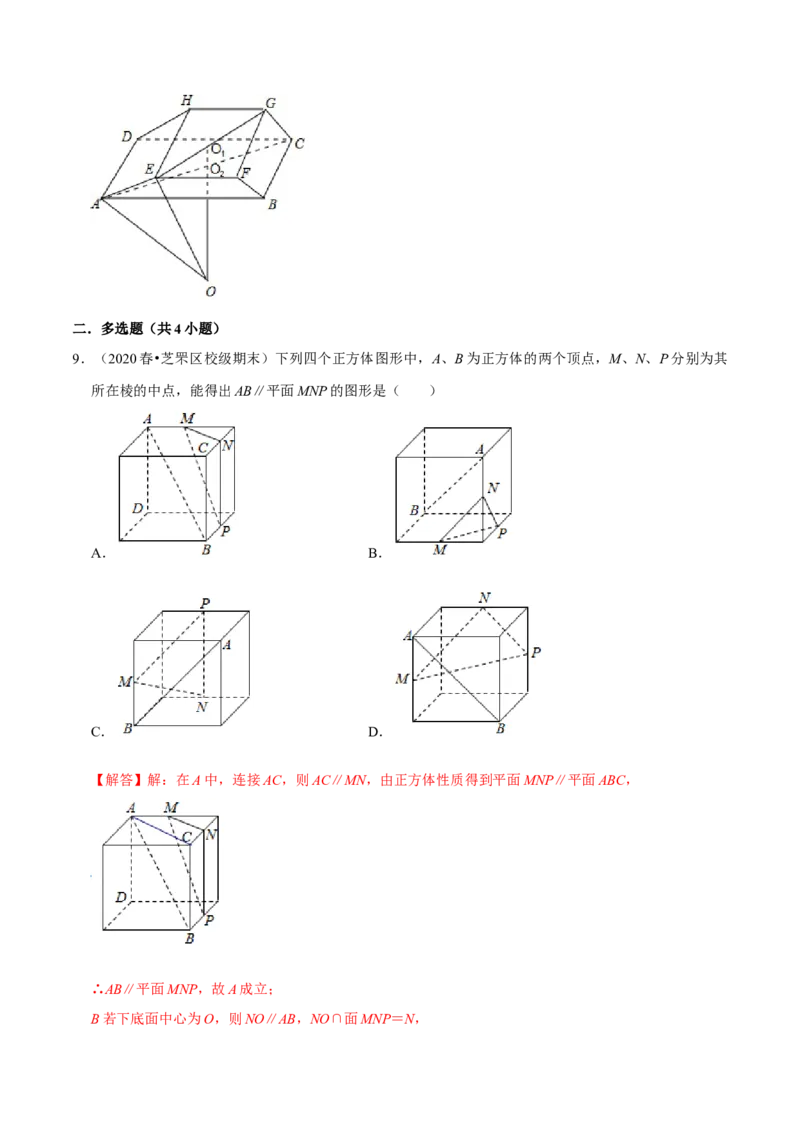
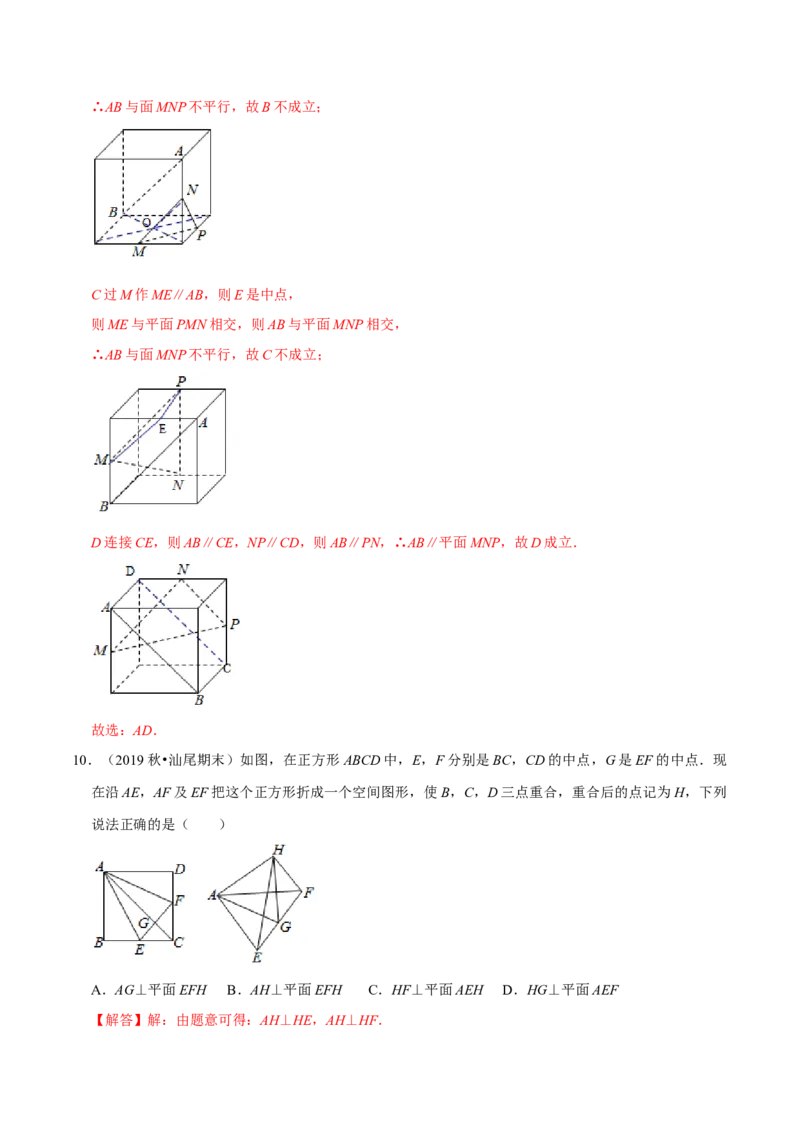
9.(2020春•芝罘区校级期末)下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其
所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B.
C. D.
【解答】解:在A中,连接AC,则AC∥MN,由正方体性质得到平面MNP∥平面ABC,
∴AB∥平面MNP,故A成立;
B若下底面中心为O,则NO∥AB,NO∩面MNP=N,∴AB与面MNP不平行,故B不成立;
C过M作ME∥AB,则E是中点,
则ME与平面PMN相交,则AB与平面MNP相交,
∴AB与面MNP不平行,故C不成立;
D连接CE,则AB∥CE,NP∥CD,则AB∥PN,∴AB∥平面MNP,故D成立.
故选:AD.
10.(2019秋•汕尾期末)如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现
在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列
说法正确的是( )
A.AG⊥平面EFH B.AH⊥平面EFH C.HF⊥平面AEH D.HG⊥平面AEF
【解答】解:由题意可得:AH⊥HE,AH⊥HF.∴AH⊥平面EFH,而AG与平面EFH不垂直.∴B正确,A不正确.
又HF⊥HE,∴HF⊥平面AHE,C正确.
HG与AG不垂直,因此HG⊥平面AEF不正确.D不正确.
故选:BC.
11.(2019春•东营期末)设m,n是两条不同的直线, , 是两个不同的平面,则下列结论正确的是(
) α β
A.若m⊥ ,n⊥ ,则m∥n
B.若m∥nα,m∥α,则n∥
C.若m ,n ,α 则m,nα是异面直线
D.若 ∥⊂α,m⊂β ,n ,则m∥n或m,n是异面直线
【解答α】解β:由⊂mα,n⊂是β两条不同的直线, , 是两个不同的平面,得:
对于A,若m⊥ ,n⊥ ,则由线面垂直的性α质β定理得m∥n,故A正确;
对于B,若m∥αn,m∥α,则n∥ 或n ,故B错误;
对于C,若m ,n ,α 则m,nα相交、⊂α平行或异面,故C错误;
对于D,若 ∥⊂α,m⊂β ,n ,则m∥n或m,n是异面直线,故D正确.
故选:AD.α β ⊂α ⊂β
12.(2020•泉州一模)已知正方体ABCD﹣A B C D 的棱长为1,E是DD 的中点,则下列选项中正确的
1 1 1 1 1
是( )
A.AC⊥B E
1
B.B C∥平面A BD
1 1
C.三棱锥C ﹣B CE的体积为
1 1
D.异面直线B C与BD所成的角为45°
1
【解答】解:如图,
∵AC⊥BD,AC⊥BB ,∴AC⊥平面BB D D,
1 1 1又B E 平面BB D D,∴AC⊥B E,故A正确;
1 1 1 1
∵B C∥⊂A D,A D 平面A BD,B C 平面A BD,∴B C∥平面A BD,故B正确;
1 1 1 1 1 1 1 1
⊂ ⊄
三棱锥C ﹣B CE的体积为 ,故C错误;
1 1
∵BD∥B D ,∴∠CB D 是异面直线B C与BD所成的角,又△CB D 是等边三角形,
1 1 1 1 1 1 1
∴异面直线B C与BD所成的角为60°,故D错误.
1
故选:AB.
三.填空题(共4小题)
13.(2020•中卫二模)已知三棱锥O﹣ABC中,A,B,C三点在以O为球心的球面上,若AB=BC=2,
∠ABC=120°,且三棱锥O﹣ABC的体积为 ,则球O的表面积为 5 2 .
【解答】解:如图所示 设△ABC的外接圆的圆心为O 1 ,半径为r, π
在△ABC中,由余弦定理可得:
|AC| 2 ,∵2r 4,
解得:r=2.
又由题知S△ABC 2×2×sin120° ,
又三棱锥O﹣ABC的体积为 S△ABC •|OO
1
|,
所以棱锥O﹣ABC的高|OO |=3,∴球O的半径R ,
1
∴球O的表面积为4 R2=52 .
故答案为:52 . π π
π
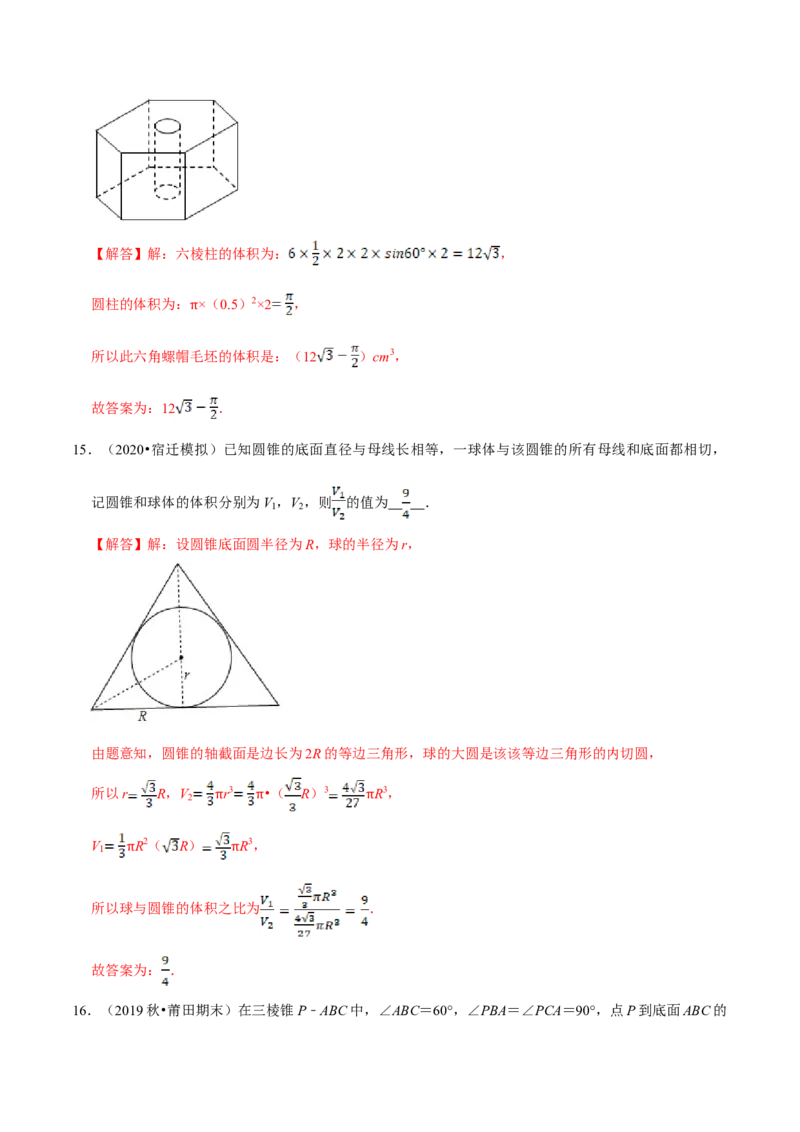
14.(2020•江苏)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六
边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是 1 2 cm3.【解答】解:六棱柱的体积为: ,
圆柱的体积为: ×(0.5)2×2 ,
π
所以此六角螺帽毛坯的体积是:(12 )cm3,
故答案为:12 .
15.(2020•宿迁模拟)已知圆锥的底面直径与母线长相等,一球体与该圆锥的所有母线和底面都相切,
记圆锥和球体的体积分别为V ,V ,则 的值为 .
1 2
【解答】解:设圆锥底面圆半径为R,球的半径为r,
由题意知,圆锥的轴截面是边长为2R的等边三角形,球的大圆是该该等边三角形的内切圆,
所以r R,V r3 •( R)3 R3,
2
π π π
V R2( R) R3,
1
π π
所以球与圆锥的体积之比为 .
故答案为: .
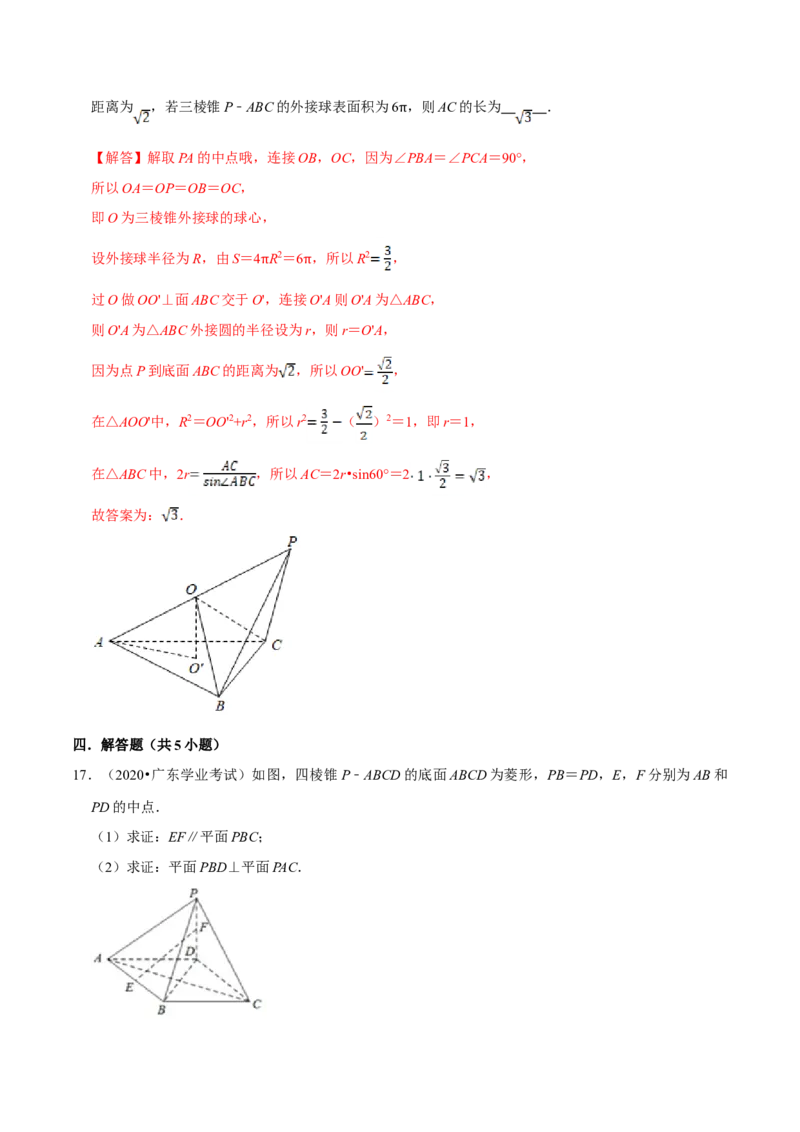
16.(2019秋•莆田期末)在三棱锥P﹣ABC中,∠ABC=60°,∠PBA=∠PCA=90°,点P到底面ABC的距离为 ,若三棱锥P﹣ABC的外接球表面积为6 ,则AC的长为 .
π
【解答】解取PA的中点哦,连接OB,OC,因为∠PBA=∠PCA=90°,
所以OA=OP=OB=OC,
即O为三棱锥外接球的球心,
设外接球半径为R,由S=4 R2=6 ,所以R2 ,
π π
过O做OO'⊥面ABC交于O',连接O'A则O'A为△ABC,
则O'A为△ABC外接圆的半径设为r,则r=O'A,
因为点P到底面ABC的距离为 ,所以OO' ,
在△AOO'中,R2=OO'2+r2,所以r2 ( )2=1,即r=1,
在△ABC中,2r ,所以AC=2r•sin60°=2 ,
故答案为: .
四.解答题(共5小题)
17.(2020•广东学业考试)如图,四棱锥P﹣ABCD的底面ABCD为菱形,PB=PD,E,F分别为AB和
PD的中点.
(1)求证:EF∥平面PBC;
(2)求证:平面PBD⊥平面PAC.【解答】证明:(1)取PC的中点G,
∵F是PD的中点,
∴FG∥CD,且FG CD,
又∵底面ABCD是菱形,E是AB中点,
∴BE∥CD,且BE CD,
∴BE∥FG,且BE=FG,
∴四边形BEFG是平行四边形,
∴EF∥BG,
又EF 平面PBC,BG 平面PBC,
∴EF∥⊄平面PBC; ⊂
(2)设AC∩BD=O,则O是BD中点,
∵底面ABCD是菱形,
∴BD⊥AC,
又∵PB=PD,O是BD中点,
∴BD⊥PO,
又AC∩PO=O,AC 平面PAC,PO 平面PAC,
∴BD⊥平面PAC, ⊂ ⊂
∵BD 平面PBD,
∴平面⊂PBD⊥平面PAC.
18.(2019秋•赣州期末)在矩形ABCD中,AB=1,BC=2,E为AD的中点,如图1,将△ABE沿BE折
起,使得点A到达点P的位置(如图2),且平面PBE⊥平面BCDE
(1)证明:PB⊥平面PEC;
(2)若M为PB的中点,N为PC的中点,求三棱锥M﹣CDN的体积.【解答】解:(1)证明:由题意,易得 ,
∴BE2+CE2=BC2,即BE⊥CE,
又∵平面PBE⊥平面BCDE,交线为BE,
∴CE⊥平面PBE,
∴CE⊥PB,
又∵PB⊥PE,
∴PB⊥平面PEC;
(2)取BE中点O,连接PO,
∵PB=PE,
∴PO⊥BE, ,
又∵平面PBE⊥平面BCDE,交线为BE,
∴PO⊥平面BCDE,
∵M为PB的中点,N为PC的中点,
∴ .19.(2019春•河南月考)如图所示,已知四棱锥 P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,
AB⊥BC,AB=AD=1,BC=2,PB⊥平面ABCD,PB=1.
(Ⅰ)求证:CD⊥PD;
(Ⅱ)求四棱锥P﹣ABCD的表面积.
【解答】解:(Ⅰ)证明:在梯形ABCD中,易求 ,
∵BC=2,
∴CD⊥PD,
∵PB⊥平面ABCD,CD在平面ABCD内,
∴PB⊥CD,
又PB∩BD=B,且都在平面PBD内,
∴CD⊥平面PBD,
又PD在平面PBD内,
∴CD⊥PD;
(Ⅱ)由(Ⅰ)知, ,
又∵DA∥BC,BC⊥AB,PB⊥平面ABCD,
∴△PAD,△PBA,△PCD都为直角三角形,
∴ ,
∵ ,
∴四棱锥P﹣ABCD的表面积为 .
20.(2019春•玉溪期末)如图,在三棱柱 ABC﹣A B C 中(底面△ABC为正三角形),A A⊥平面
1 1 1 1
ABC,AB=AC=2, ,D是BC边的中点.
(1)证明:平面ADB ⊥平面BB C C.
1 1 1
(2)求点B到平面ADB 的距离.
1【解答】(1)证明:∵AB=AC,D为BC的中点,∴AD⊥BC.
又BB ⊥平面ABC,AD 平面ABC,∴BB ⊥AD.
1 1
又BC∩BB =B,∴AD⊥⊂平面BB C C.
1 1 1
又AD 平面ADB ,∴平面ADB ⊥平面BB C C.
1 1 1 1
(2)解⊂:由(1)知,AD⊥平面BB
1
C
1
C,B
1
D 平面BB
1
C
1
C,∴AD⊥B
1
D. ,
∵ ,B D=2, ⊂
1
∴ , .
设点B到平面ADB 的距离为d,
1
由 ,得 ,
即 ,∴d ,即点B到平面ADB 的距离为 .
1
21.(2019秋•路南区校级期中)在直三棱柱ABC﹣A B C 中,AC=BC ,∠ACB=90°,AA =2,D
1 1 1 1
为AB的中点.
(1)求异面直线AC 与B C所成角的余弦值;
1 1
(2)在棱A B 上是否存在一点M,使得平面C AM∥平面B CD.
1 1 1 1【解答】解:(1)以C为原点,CB、CA、CC 分别为x、z、y轴建立空间直角坐标系.
1
因为AC=BC ,AA =2.
1
所以C(0,0,0),A( ),C (0,2,0), .
1
所以 ,
那么 ;
(2)在A B 上中点M,连接MA.
1 1
证明如下:
∵三棱柱ABC﹣A B C 是直三棱.
1 1 1
∴平面ABC∥平面A B C ,AB∥A B ,AB=A B .
1 1 1 1 1 1 1
∵D、M分别是AB、A B 的中点.
1 1
∴C M∥CD.
1
∵CD 平面CDB ,C M 平面CDB ,
1 1 1
∴C M⊂∥平面CDB . ⊄
1 1
∴ , .∴MB =AD,MB ∥AD.
1 1
∴四边形ADB M是平行四边形.
1
∴AM∥DB .
1
∵DB 平面DCB ,AM 平面DBC .
1 1 1
∴AM∥⊂平面DCB . ⊄
1
∵C M∩AM=M.
1
∴平面C AM∥平面B CD.
1 1