文档内容
第八章 立体几何初步B(提高卷)
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
第Ⅰ卷(选择题)
请点击修改第I卷的文字说明
评卷人 得 分
一.选择题(共8小题)
1.(2019春•辽宁期中)直角三角形的三边满足a<b<c,分别以a,b,c三边为轴将三角形旋转一周所
得旋转体的体积记为V,V ,V ,则( )
a b c
A.V <V <V B.V<V <V C.V <V<V D.V <V<V
c b a a b c c a b b a c
2.(2020•大连二模)已知三棱锥P﹣ABC,面PAB⊥面ABC,PA=PB=4, ,∠ACB=90°,则
三棱锥P﹣ABC外接球的表面积( )
A.20 B.32 C.64 D.80
3.(202π0•泰安模拟)我国古代π数学名著《九章算术》π中记载:“刍甍者,π下有袤有广,而上有袤无广.
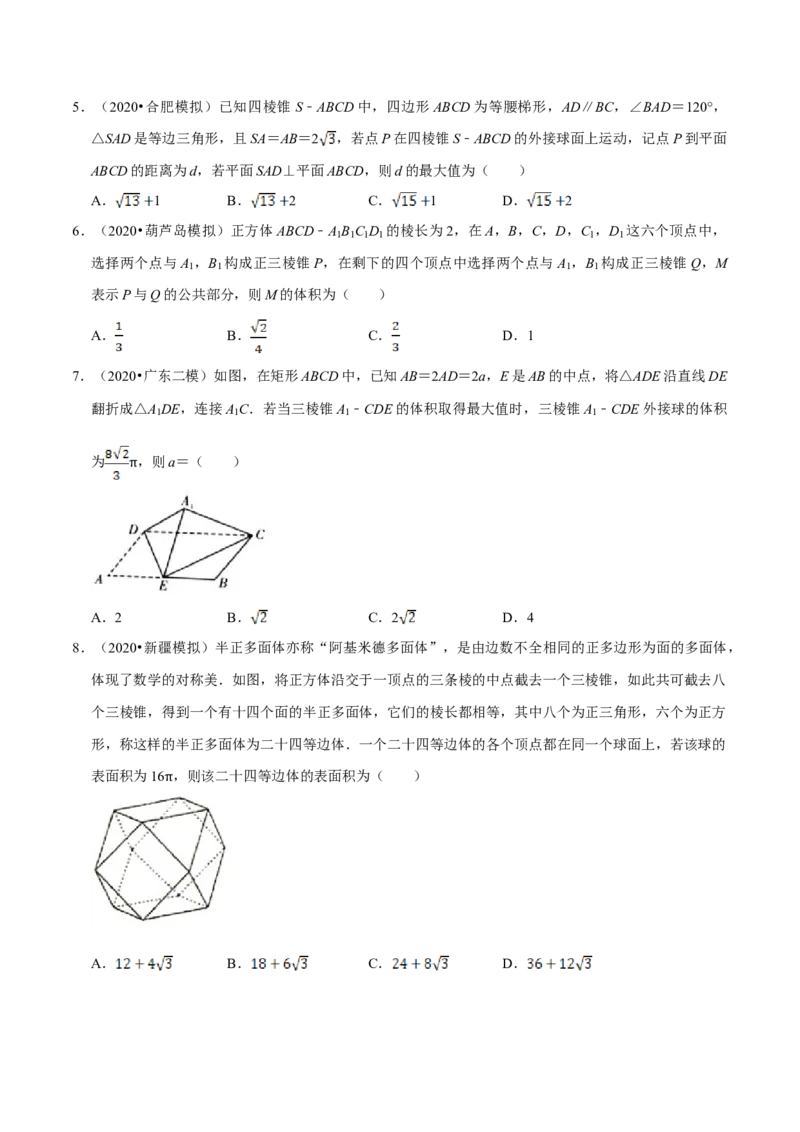
刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的
正方形,上棱 ,EF∥平面ABCD,EF与平面ABCD的距离为2,该刍甍的体积为( )
A.6 B. C. D.12
4.(2020•全国Ⅰ卷模拟)已知O为等腰直角三角形POD的直角顶点,以OP为旋转轴旋转一周得到几何
体,CD是底面圆O上的弦,△COD为等边三角形,则异面直线OC与PD所成角的余弦值为( )
A. B. C. D.5.(2020•合肥模拟)已知四棱锥 S﹣ABCD中,四边形ABCD为等腰梯形,AD∥BC,∠BAD=120°,
△SAD是等边三角形,且SA=AB=2 ,若点P在四棱锥S﹣ABCD的外接球面上运动,记点P到平面
ABCD的距离为d,若平面SAD⊥平面ABCD,则d的最大值为( )
A. 1 B. 2 C. 1 D. 2
6.(2020•葫芦岛模拟)正方体ABCD﹣A B C D 的棱长为2,在A,B,C,D,C ,D 这六个顶点中,
1 1 1 1 1 1
选择两个点与A ,B 构成正三棱锥P,在剩下的四个顶点中选择两个点与 A ,B 构成正三棱锥Q,M
1 1 1 1
表示P与Q的公共部分,则M的体积为( )
A. B. C. D.1
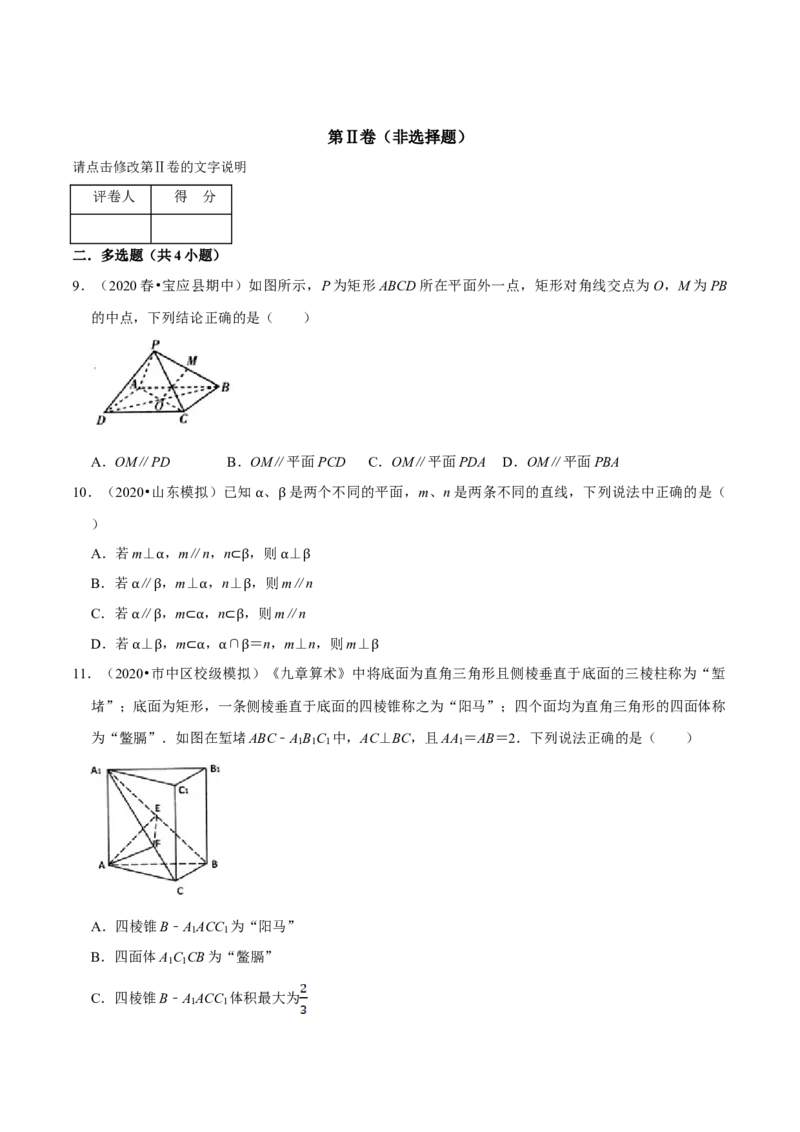
7.(2020•广东二模)如图,在矩形ABCD中,已知AB=2AD=2a,E是AB的中点,将△ADE沿直线DE
翻折成△A DE,连接A C.若当三棱锥A ﹣CDE的体积取得最大值时,三棱锥A ﹣CDE外接球的体积
1 1 1 1
为 ,则a=( )
π
A.2 B. C.2 D.4
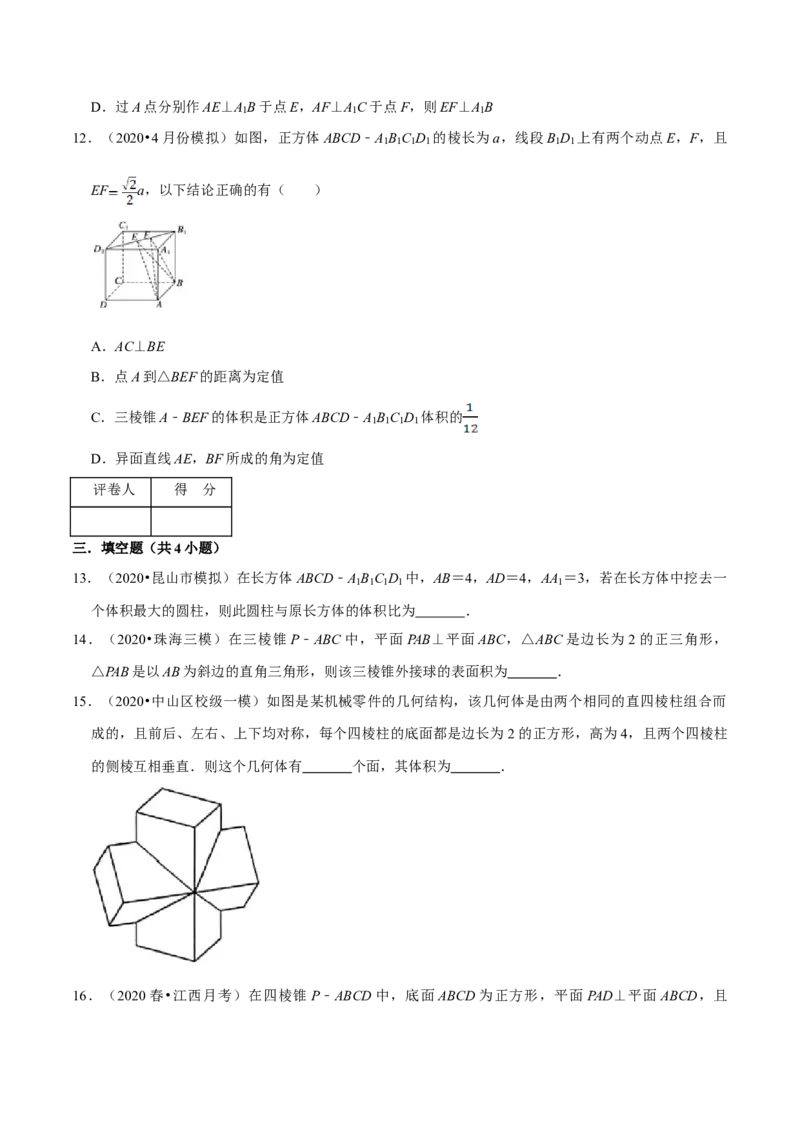
8.(2020•新疆模拟)半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,
体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八
个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方
形,称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上,若该球的
表面积为16 ,则该二十四等边体的表面积为( )
π
A. B. C. D.第Ⅱ卷(非选择题)
请点击修改第Ⅱ卷的文字说明
评卷人 得 分
二.多选题(共4小题)
9.(2020春•宝应县期中)如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB
的中点,下列结论正确的是( )
A.OM∥PD B.OM∥平面PCD C.OM∥平面PDA D.OM∥平面PBA
10.(2020•山东模拟)已知 、 是两个不同的平面,m、n是两条不同的直线,下列说法中正确的是(
) α β
A.若m⊥ ,m∥n,n ,则 ⊥
B.若 ∥α,m⊥ ,n⊥⊂β,则αm∥βn
C.若α∥β,m α,n β,则m∥n
D.若α⊥β,m⊂α, ⊂∩β =n,m⊥n,则m⊥
11.(202α0•市β中区⊂校α级α模拟β)《九章算术》中将β底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑
堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称
为“鳖膈”.如图在堑堵ABC﹣A B C 中,AC⊥BC,且AA =AB=2.下列说法正确的是( )
1 1 1 1
A.四棱锥B﹣A ACC 为“阳马”
1 1
B.四面体A C CB为“鳖膈”
1 1
C.四棱锥B﹣A ACC 体积最大为
1 1D.过A点分别作AE⊥A B于点E,AF⊥A C于点F,则EF⊥A B
1 1 1
12.(2020•4月份模拟)如图,正方体ABCD﹣A B C D 的棱长为a,线段B D 上有两个动点E,F,且
1 1 1 1 1 1
EF a,以下结论正确的有( )
A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣A B C D 体积的
1 1 1 1
D.异面直线AE,BF所成的角为定值
评卷人 得 分
三.填空题(共4小题)
13.(2020•昆山市模拟)在长方体ABCD﹣A B C D 中,AB=4,AD=4,AA =3,若在长方体中挖去一
1 1 1 1 1
个体积最大的圆柱,则此圆柱与原长方体的体积比为 .
14.(2020•珠海三模)在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△ABC是边长为2的正三角形,
△PAB是以AB为斜边的直角三角形,则该三棱锥外接球的表面积为 .
15.(2020•中山区校级一模)如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而
成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为 2的正方形,高为4,且两个四棱柱
的侧棱互相垂直.则这个几何体有 个面,其体积为 .
16.(2020春•江西月考)在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,且△PAD为等边三角形,若四棱锥P﹣ABCD的体积与四棱锥P﹣ABCD外接球的表面积大小之比为 ,
则正方形ABCD的边长为 .
评卷人 得 分
四.解答题(共5小题)
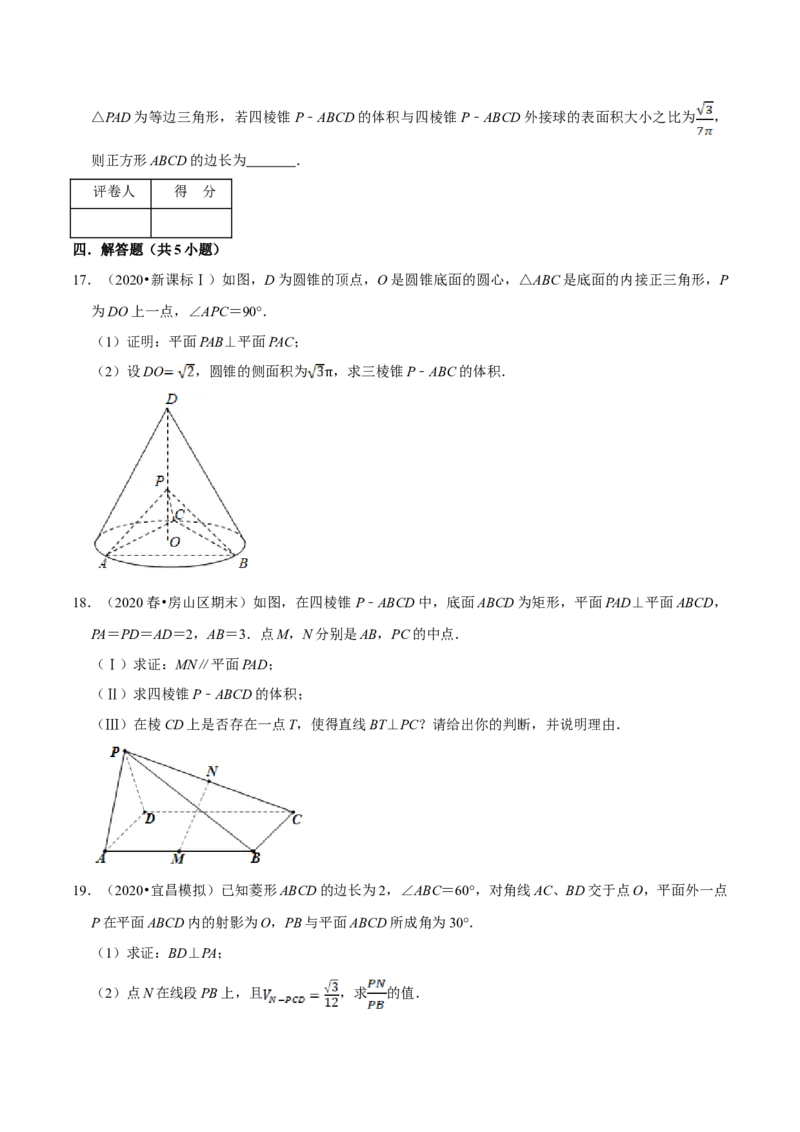
17.(2020•新课标Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P
为DO上一点,∠APC=90°.
(1)证明:平面PAB⊥平面PAC;
(2)设DO ,圆锥的侧面积为 ,求三棱锥P﹣ABC的体积.
π
18.(2020春•房山区期末)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,
PA=PD=AD=2,AB=3.点M,N分别是AB,PC的中点.
(Ⅰ)求证:MN∥平面PAD;
(Ⅱ)求四棱锥P﹣ABCD的体积;
(Ⅲ)在棱CD上是否存在一点T,使得直线BT⊥PC?请给出你的判断,并说明理由.
19.(2020•宜昌模拟)已知菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O,平面外一点
P在平面ABCD内的射影为O,PB与平面ABCD所成角为30°.
(1)求证:BD⊥PA;
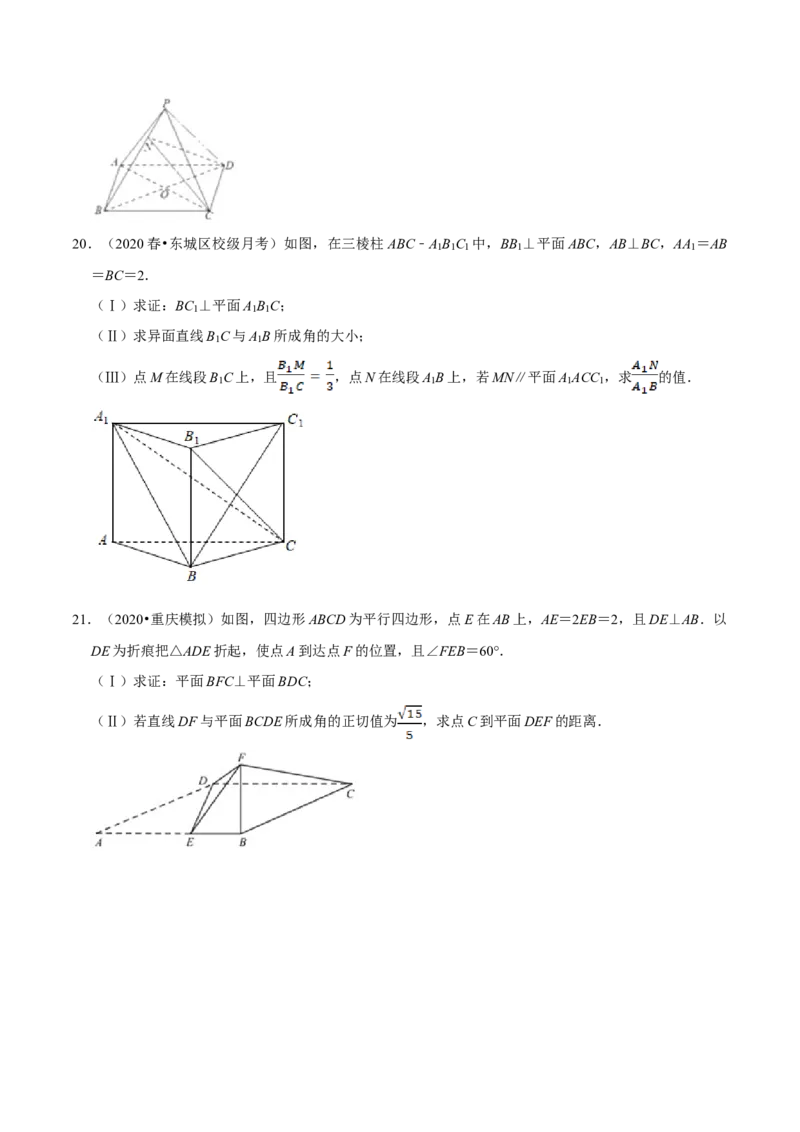
(2)点N在线段PB上,且 ,求 的值.20.(2020春•东城区校级月考)如图,在三棱柱ABC﹣A B C 中,BB ⊥平面ABC,AB⊥BC,AA =AB
1 1 1 1 1
=BC=2.
(Ⅰ)求证:BC ⊥平面A B C;
1 1 1
(Ⅱ)求异面直线B C与A B所成角的大小;
1 1
(Ⅲ)点M在线段B C上,且 ,点N在线段A B上,若MN∥平面A ACC ,求 的值.
1 1 1 1
21.(2020•重庆模拟)如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以
DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
(Ⅰ)求证:平面BFC⊥平面BDC;
(Ⅱ)若直线DF与平面BCDE所成角的正切值为 ,求点C到平面DEF的距离.