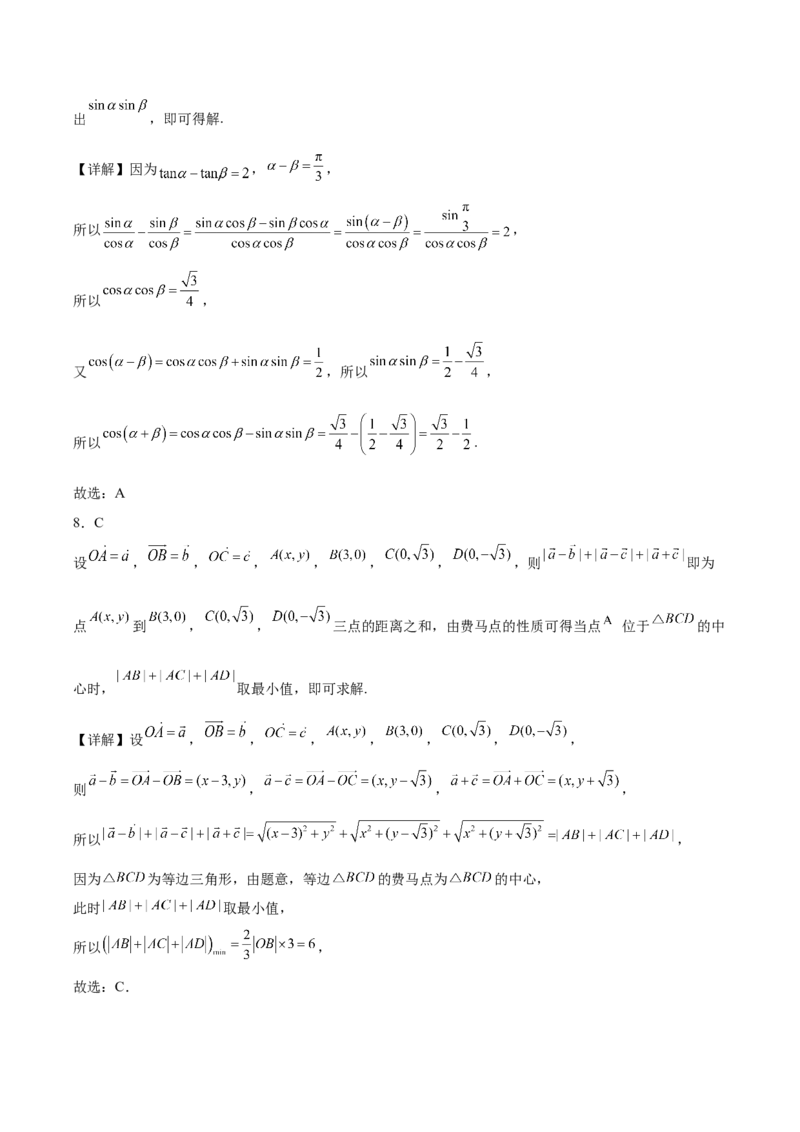文档内容
江苏省泰州中学2024-2025学年高一下学期4月期中
数学试题
一、单选题
1.下列命题是真命题的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
2.若 , ,则 ( )
A. B. C. D.
3.函数 的图象大致为( )
A. B. C.
D.4.“ ”是“向量 , ,则 ”的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
5.某学校生物兴趣小组同学自制生态瓶,根据水中的生物种类数S与生物个体总数N研究生态瓶水质,
设立生物丰富度指数 作为生态瓶水质评价指标.生物丰富度指数d越大,水质越好.若经过老师指导
调整以后生态瓶生物种类数S没有变化,生物个体总数由 变为 ,生物丰富度指数由 提高到 ,
则( )
A. B.
C. D.
6.在正方形 中,点E满足 ,点F满足 ,若 ,则
( )
A. B. C. D.
7.已知 , ,则 的值是( )
A. B. C. D.
8.若 的三个内角均小于120°,点 满足 ,则点 到三角形三个顶
点的距离之和最小,点 被人们称为费马点.根据以上性质,已知 是平面内的任意一个向量,向量 ,
满足 ,且 , ,则 的最小值是( )
A.9 B. C.6 D.
二、多选题
9.下列各式的值为1的是( )
A. B.C. D.
10.已知曲线 ( 且 )过定点 ,且 的坐标满足方程 ,则
( )
A. 的最大值为 B. 的最小值为
C. 的最小值为 D. 的最小值为
11.对于函数 ,若对于其定义域 中任意给定的实数 ,都有 ,并且 ,则
称函数 为倒函数.以下选项正确的有( )
A.函数 是倒函数
B.函数 是倒函数
C.若 是 上的倒函数,当 时, ,方程 没有正整数解
D.若 是 上的倒函数,其函数值恒大于0,且在 上是增函数.记 ,则
是 的充要条件
三、填空题
12.幂函数为什么叫“幂函数”呢?幂,本义为方布.三国时的刘徽为《九章算术·方田》作注:“田幂,
凡广(即长)从(即宽)相乘谓之乘.”幂字之义由长方形的布引申成长方形的面积;明代徐光启翻译《几
何原本》时,自注曰:“自乘之数曰幂”.幂字之义由长方形的面积再引申成相同的数相乘,即 ,函数
为幂函数,则 .
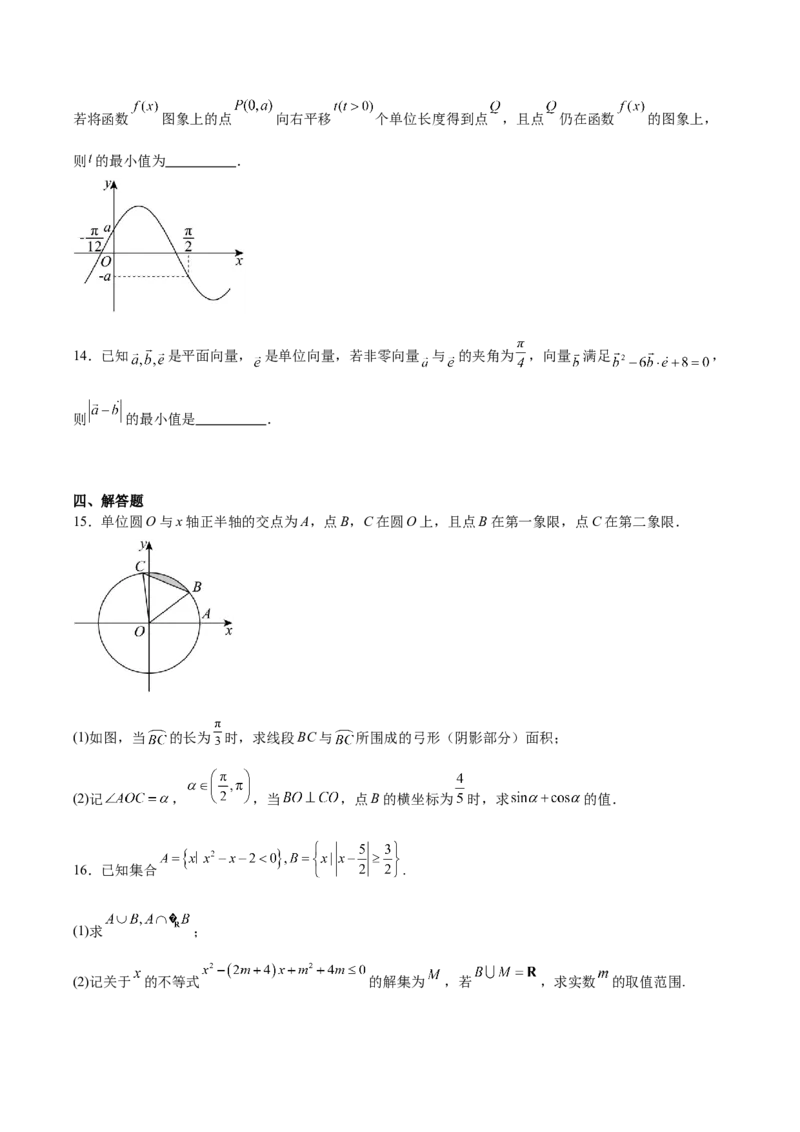
13.已知函数 ( , 为常数, )的部分图象如图所示.则 ;若将函数 图象上的点 向右平移 个单位长度得到点 ,且点 仍在函数 的图象上,
则 的最小值为 .
14.已知 是平面向量, 是单位向量,若非零向量 与 的夹角为 ,向量 满足 ,
则 的最小值是 .
四、解答题
15.单位圆O与x轴正半轴的交点为A,点B,C在圆O上,且点B在第一象限,点C在第二象限.
(1)如图,当 的长为 时,求线段BC与 所围成的弓形(阴影部分)面积;
(2)记 , ,当 ,点B的横坐标为 时,求 的值.
16.已知集合 .
(1)求 ;
(2)记关于 的不等式 的解集为 ,若 ,求实数 的取值范围.17.已知函数 在R上为奇函数, .
(1)求实数 的值;
(2)指出函数 的单调性(说明理由,不需要证明);
(3)设对任意 ,都有 成立,求 的取值范围.
18.已知向量 , ,函数
, .
(1)若 的最小值为-1,求实数 的值;
(2)是否存在实数 ,使函数 , 有四个不同的零点?若存在,求出 的
取值范围;若不存在,请说明理由.
19.设函数 的定义域为D,对于区间 ,若满足以下两条性质之一,则称I为
的一个“ 区间”.
性质1:对任意 ,有 ;
性质2:对任意 ,有 .
(1)分别判断区间 是否为下列两函数的“ 区间”(直接写出结论);
① ; ② ;
(2)若 是函数 的“ 区间”,求m的取值范围;
(3)已知定义在 上,且图象连续不断的函数 满足:对任意 ,且 ,有.求证: 存在“ 区间”,且存在 ,使得 不属于 的所有“ 区间”.题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A D D A C BC ACD
题号 11
答案 ACD
1.A
由倒数定义易判断A正确;通过举反例即可逐一排除B,C,D项.
【详解】对于A,由 可知 均不为0,故 ,即A正确;
对于B,由 可得 或 ,故B错误;
对于C, 由 ,若取 ,则 没有意义,故C错误;
对于D,由 ,若取 ,则 ,故D错误.
故选:A.
2.C
先化简集合A,B,再利用集合的交集运算求解.
【详解】解: 或 ,
,
,
故选:C
3.B
先求函数定义域,排除A,再根据函数奇偶性排除B,再通过特殊值排除D得答案.
【详解】函数 的定义域为 且 ,排除A项;
∵ ,∴ 是奇函数,排除C项;
再取特殊值当 时, ,排除D项.
故选:B.4.A
由于 ,即可判定
【详解】由题意,
因此“ ”是“向量 , ,则 ”的充分不必要条件
故选:A
5.D
根据公式列出调整前后的生物丰富度指数表达式,对①②式进行变形,根据对数运算得出答案.
【详解】由题意得 ①, ②,
则 ,
即 ,即 ,
所以 ,
故选:D
6.D
根据给定条件,利用向量线性运算,结合平面向量基本定理求解即得.
【详解】在正方形 中, ,
由 ,得 ,又 ,
因此
,
而 ,且 不共线,于是 .
故选:D
7.A
由 将切化弦,再通分,结合两角差的正弦公式求出 ,再由两角差的余弦公式求出 ,即可得解.
【详解】因为 , ,
所以 ,
所以 ,
又 ,所以 ,
所以 .
故选:A
8.C
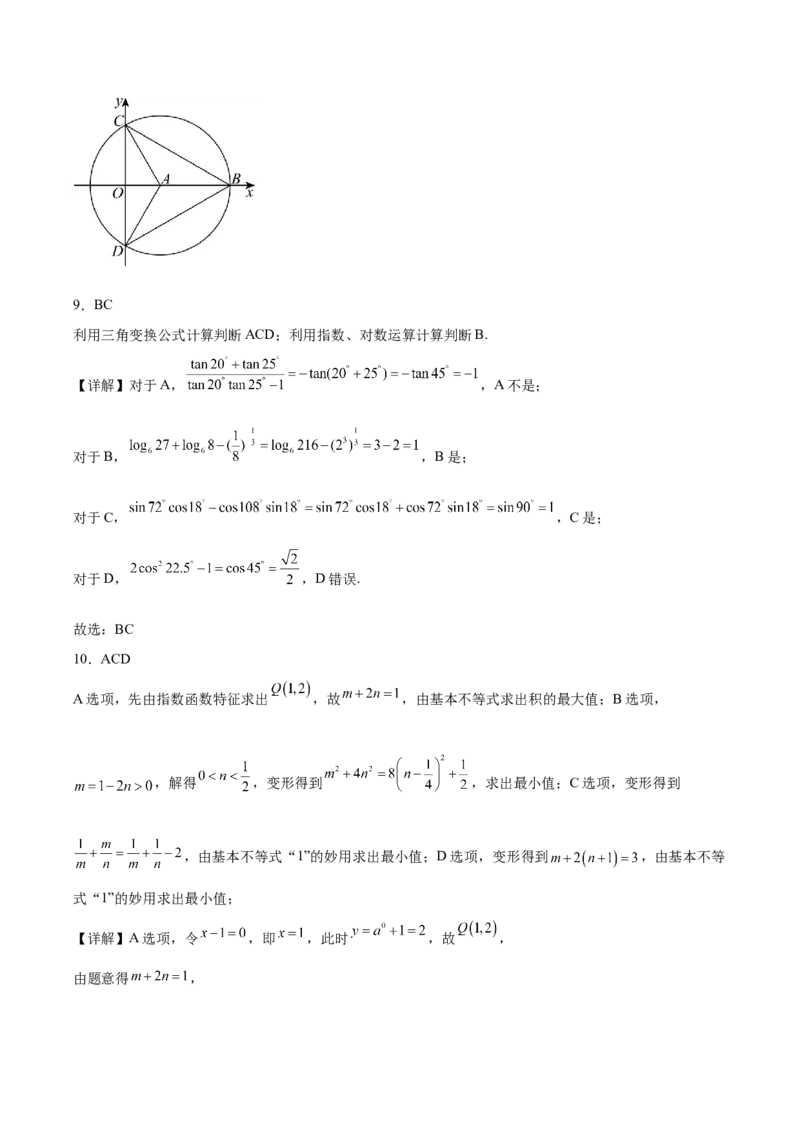
设 , , , , , , ,则 即为
点 到 , , 三点的距离之和,由费马点的性质可得当点 位于 的中
心时, 取最小值,即可求解.
【详解】设 , , , , , , ,
则 , , ,
所以 ,
因为 为等边三角形,由题意,等边 的费马点为 的中心,
此时 取最小值,
所以 ,
故选:C.9.BC
利用三角变换公式计算判断ACD;利用指数、对数运算计算判断B.
【详解】对于A, ,A不是;
对于B, ,B是;
对于C, ,C是;
对于D, ,D错误.
故选:BC
10.ACD
A选项,先由指数函数特征求出 ,故 ,由基本不等式求出积的最大值;B选项,
,解得 ,变形得到 ,求出最小值;C选项,变形得到
,由基本不等式“1”的妙用求出最小值;D选项,变形得到 ,由基本不等
式“1”的妙用求出最小值;
【详解】A选项,令 ,即 ,此时 ,故 ,
由题意得 ,由基本不等式得 ,即 ,解得 ,
当且仅当 ,即 时,等号成立,A正确;
B选项, ,故 ,解得 ,
则 ,
故当 时, 取得最小值,最小值为 ,B错误;
C选项, ,
因为 , ,
所以 ,
当且仅当 ,即 时,等号成立,
故 的最小值为 ,C正确;
D选项,因为 , ,
所以 ,
故
,
当且仅当 ,即 时,等号成立,D正确.
故选:ACD.
11.ACD
对于选项A、B,直接根据定义判断函数是否为倒函数;对于选项C,先根据倒函数性质求出 时函数表达式,再判断方程是否有正整数解;对于选项D,根据函数单调性判断 与 之
间的充分性和必要性.
【详解】对于A,对于 定义域为 ,显然定义域中任意实数 ,都有 成立,又
,所以 是倒函数.故A正确.
对于B, 定义域为 ,当 时, ,不符合倒函数的定义,所以
不是倒函数,故B错误.
对于C,令 ,则 ,由倒函数的定义,可得 ,
所以 ,所以 ,要使 有正整数解,
则 ,当 时, ;
当 时, ;所以 没有正整数解,故C正确.
对于D,充分性:当 时, 且 ,因为 是增函数,
所以 , ,即 , ,
所以 .
必要性:当 时,
有 ,
因为 恒大于0,所以 ,即 ,所以 ,因为 是增函数,所以 ,即 ;
综上可得 是 的充要条件,故D正确.
故选:ACD.
12.
利用幂函数的定义进行求解即可得.
【详解】解:因为函数 为幂函数,
所以可得 ,解得 .
故答案为:1
13. 0 /
根据给定条件,求出函数 的解析式,并求出 值,再由 求出 的关系式即可得解.
【详解】观察函数图象,得函数 的周期 , ,则 ,
由 ,且函数 的图象在点 附近是上升的,得 ,
即 ,因此 ,所以 ;
,而点 在 的图象上,则 ,即 ,
又 ,则 或 ,解得 或 ,
所以 的最小值为 .
故答案为:0;
14.
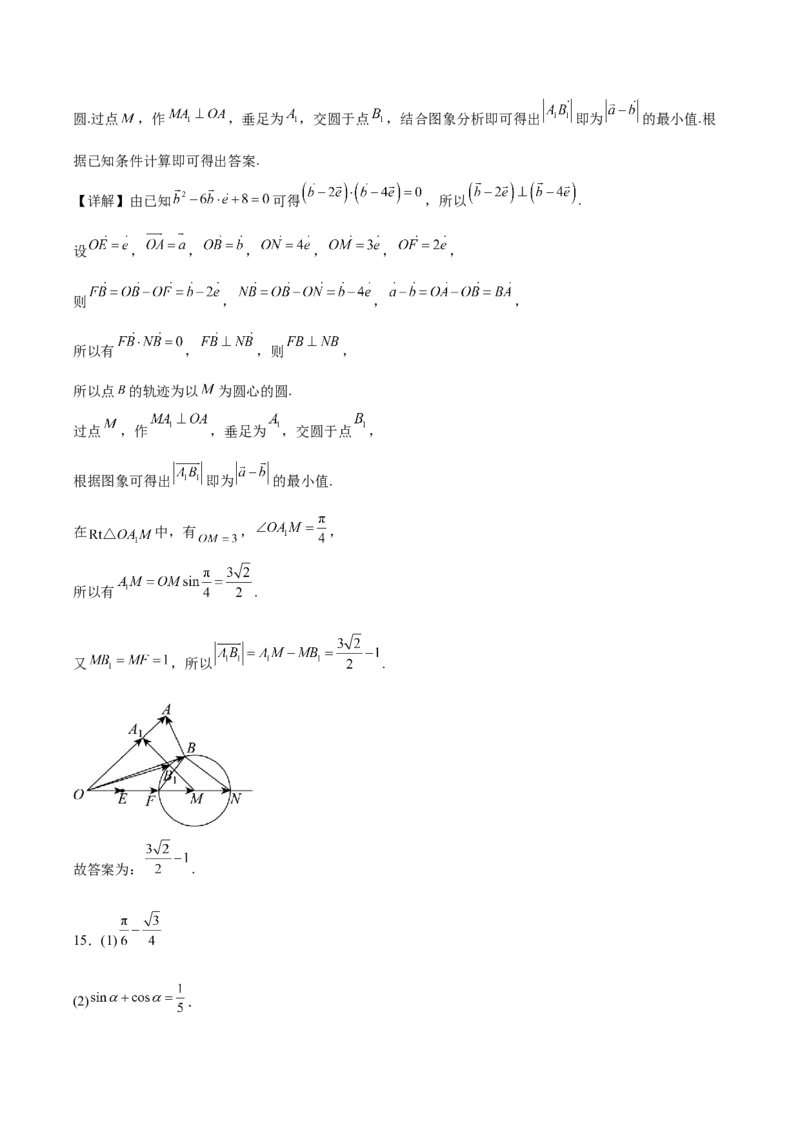
根据已知 可得出 .进而作图推得 ,点 的轨迹为以 为圆心的圆.过点 ,作 ,垂足为 ,交圆于点 ,结合图象分析即可得出 即为 的最小值.根
据已知条件计算即可得出答案.
【详解】由已知 可得 ,所以 .
设 , , , , , ,
则 , , ,
所以有 , ,则 ,
所以点 的轨迹为以 为圆心的圆.
过点 ,作 ,垂足为 ,交圆于点 ,
根据图象可得出 即为 的最小值.
在 中,有 , ,
所以有 .
又 ,所以 .
故答案为: .
15.(1)
(2) .(1)设弧长及圆心角,应用扇形面积公式计算 求解即可;
(2)先由已知得 进而得出 , ,最后应用诱导公式计算求解即可.
【详解】(1)设 所对的圆心角为 ,弧长为l,弓形的面积为S.
因为 ,圆O的半径为 ,所以 ,
, , .
(2)设 ,由题知 ,
于是 , ,
.即 .
16.(1) 或 ,
(2)
(1)分别解一元二次不等式和绝对值不等式,化简集合 ,再求 即可;
(2)解一元二次不等式求出集合 ,再根据 ,借助数轴可解出实数 的取值范围.
【详解】(1)解:因为 即 ,
所以 ,所以 ;
由 ,可得 或 ,
所以 或 ,进而可得 ,
所以 或 , .(2)解:因为 ,
所以 ,所以 ,
所以 ;
又 或 ,
若 ,则 ,所以 ,
所以实数 的取值范围是
17.(1)
(2) 在R上单调递减
(3)
(1)根据已知结合奇函数的性质有 ,代入化简可得 ,即有
,解出 的值,代入检验即可得出答案;
(2)令 ,分 以及 两种情况分析得出函数 的单调性,进而即
可根据复合函数的单调性得出判断;
(3)根据函数的奇偶性、单调性结合已知条件化简得出 .设
,根据已知条件结合三角函数的性质求出函数 的最小值,进而得出不等式
,求解即可得出答案.
【详解】(1)由已知结合奇函数的性质可得 ,
即,
所以 ,解得 (舍去负值),所以 .
此时有 ,定义域为R,满足题意.
(2)令 ,
因为 ,所以函数 在 上单调递增.
又当 时,有 在 上单调递
减;
当 时, 与 均为减函数,
所以有 在 上单调递减.
综上所述, 在R上单调递减.
根据复合函数的单调性可知, 在R上单调递减.
(3)由已知 ,
结合奇函数的性质可得 .
又由(2)知, 在R上单调递减,
所以有 ,整理即有 .
设 ,要使该式恒成立,则应满足 .
又 ,当 ,即 时, 有最小值 ,
则有 ,整理可得 ,解得 .
18.(1) ;(2) .
【详解】试题分析:(1)利用向量数量积的公式化简函数 即可.
(2)求出函数 的表达式,利用换元法结合一元二次函数的最值性质进行讨论求解即可.
(3)由 =0得到方程的根,利用三角函数的性质进行求解即可.
试题解析:
(1)∵ ,
,
∴ ,
∵ ∴ ,
,令 ,
∴ ∵ ,对称轴为 ,
①当 即 时,当 时, ∴ 舍,
②当 即 时,当 时, ∴ ,
③当 即 是,当 时, ∴ 舍,
综上, .(2)令 ,即 ,
∴ 或 ,∵ , 有四个不同的零点,
∴方程 和 在 上共有四个不同的实根,
∴ ∴ ∴ .
19.(1)①是,②不是;
(2) ;
(3)证明见解析.
(1)根据新定义直接判断即可得出结论;
(2)根据 是函数 的“ 区间”确定其满足性质1,据此分类讨论求二次函数值
域,检验即可得解;
(3)由所给函数性质分析出满足性质2,转化为 不恒成立, 存在“ 区间”,再构造函数
,证明有唯一零点,且 .
【详解】(1)对①,当 , ,满足性质1, 是函数的“ 区间”,
对②,当 时, ,当 时, ,故不满足性质1,2,
不是函数的“ 区间”.
(2)记 , ,注意到 ,
因此,若 为函数 的“ 区间”,则其不满足性质②,必满足性质①,即 .当 时, 在 上单调递增,且 ,
所以 不包含于 ,不合题意;
当 时, ,符合题意;
当 时, ,所以 ,不合题意.
综上, .
(3)对于任意区间 ,记 ,
依题意, 在 上单调递减,则 .
因为 ,所以 ,
即S的长度大于 的长度,故不满足性质①.
因此,如果 为 的“Q区间”,只能满足性质②,即 ,
即只需存在 使得 ,或存在 使得 .
因为 不恒成立,所以上述条件满足,所以 一定存在“Q区间" .
记 ,先证明函数 有唯一零点;
因为 在 上单调递减,所以 在 上单调递减.
若 ,则 为 的唯一零点;
若 ,则 ,即 ,
由零点存在定理,结合 单调性,可知存在唯一 ,使得 ;
若 ,则 ,即 ,
由零点存在定理,结合 单调性,可知存在唯一 ,使得 ;综上,函数 有唯一零点 ,即 ,