文档内容
第九章 统计B(提高卷)
参考答案与试题解析
一.选择题(共8小题)
1.(2020•福田区校级模拟)某校举行“我和我的祖国”文艺汇演,需征集20名志愿者参与活动服务工作,
现决定采取分层抽样的方式从“摄影协会”、“记者协会”、“管理爱好者协会”中抽取,已知三个协
会的人数比为5:2:3,且每个人被抽取的概率为0.2,则该校“摄影协会”的人数为( )
A.10 B.20 C.50 D.100
【解答】解:由题意知从“摄影协会”抽取的人数为 ,
因为每个人被抽取的概率为0.2,
故该校“摄影协会”的人数为 .
故选:C.
2.(2019春•楚雄州期中)为了检验某厂生产的取暖器是否合格,先从 500台取暖器中取50台进行检验,
用随机数表抽取样本,将500台取暖器编号为001,002,…,500.如图提供了随机数表第7行至第9
行的数据:
若从表中第7行第4列开始向右依次读取3个数据,则抽出第4台取暖器的编号为( )
A.217 B.206 C.245 D.212
【解答】解:由题意,根据简单的随机抽样的方法,
利用随机数表从第7行的第4列开始向右读取,
依次为217,157,245,217,206,由于217重复,
所以第4台取暖器的编号为206.
故选:B.
3.(2020•唐山二模)某科考试成绩公布后,发现判错一道题,经修改后重新公布,如表是抽取10名学生
的成绩,依据这些信息修改后的成绩与修改前的相比,这10名学生成绩的( )
学生学号 1 2 3 4 5 6 7 8 9 10
修改前成绩 126 130 104 100 133 123 100 120 139 103
修改后成绩 126 135 99 100 138 123 95 120 144 98A.平均分、方差都变小 B.平均分、方差都变大
C.平均分不变、方差变小 D.平均分不变、方差变大
【解答】解:经计算,修改前后的平均数均为117.8,故可排除AB,
又经计算修改前的方差为 (8.22+12.22+13.82+17.82+15.22+5.22+17.82+2.22+21.22+14.82)=197.16
修改后的方差为 (8.22+17.22+18.82+17.82+20.22+5.22+22.82+2.22+26.22+19.82)=307.16,
故选:D.
4.(2020•贵州模拟)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中
国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100名学生,其中阅读
过《西游记》的学生有70位,只阅读过《红楼梦》的学生有20位,则既没阅读过《西游记》也没阅读
过《红楼梦》的学生人数与该校学生总数比值的估计值为( )
A.0.1 B.0.2 C.0.3 D.0.4
【解答】解:∵随机调查了100名学生,其中阅读过《西游记》的学生有70位,∴没有阅读过《西游
记》的学生有100﹣70=30位.
∵只阅读过《红楼梦》的学生有20位,
则既没阅读过《西游记》也没阅读过《红楼梦》的学生人数为30﹣20=10人,
则既没阅读过《西游记》也没阅读过《红楼梦》的学生人数与该校学生总数比值的估计值为 0.1,
故选:A.
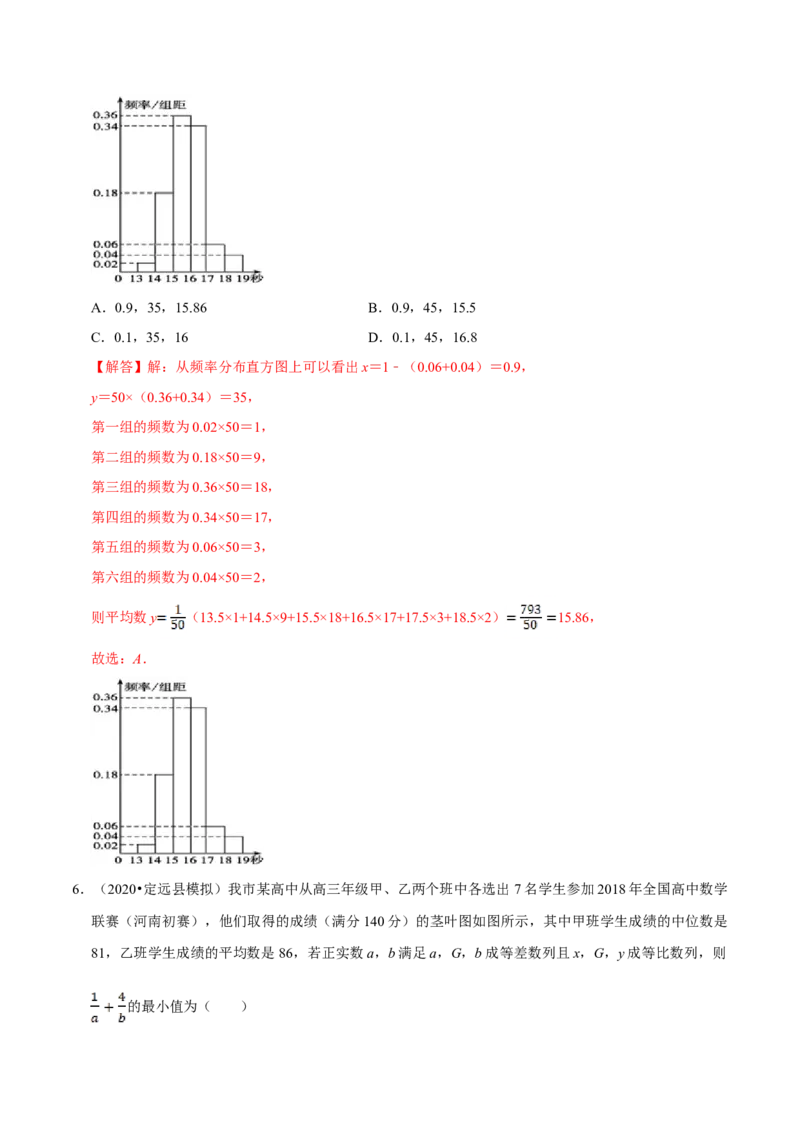
5.(2019春•眉山期末)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果
按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于
15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.
设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为
y,平均成绩为z,则从频率分布直方图中可分析出x、y、z的值分别为( )A.0.9,35,15.86 B.0.9,45,15.5
C.0.1,35,16 D.0.1,45,16.8
【解答】解:从频率分布直方图上可以看出x=1﹣(0.06+0.04)=0.9,
y=50×(0.36+0.34)=35,
第一组的频数为0.02×50=1,
第二组的频数为0.18×50=9,
第三组的频数为0.36×50=18,
第四组的频数为0.34×50=17,
第五组的频数为0.06×50=3,
第六组的频数为0.04×50=2,
则平均数y (13.5×1+14.5×9+15.5×18+16.5×17+17.5×3+18.5×2) 15.86,
故选:A.
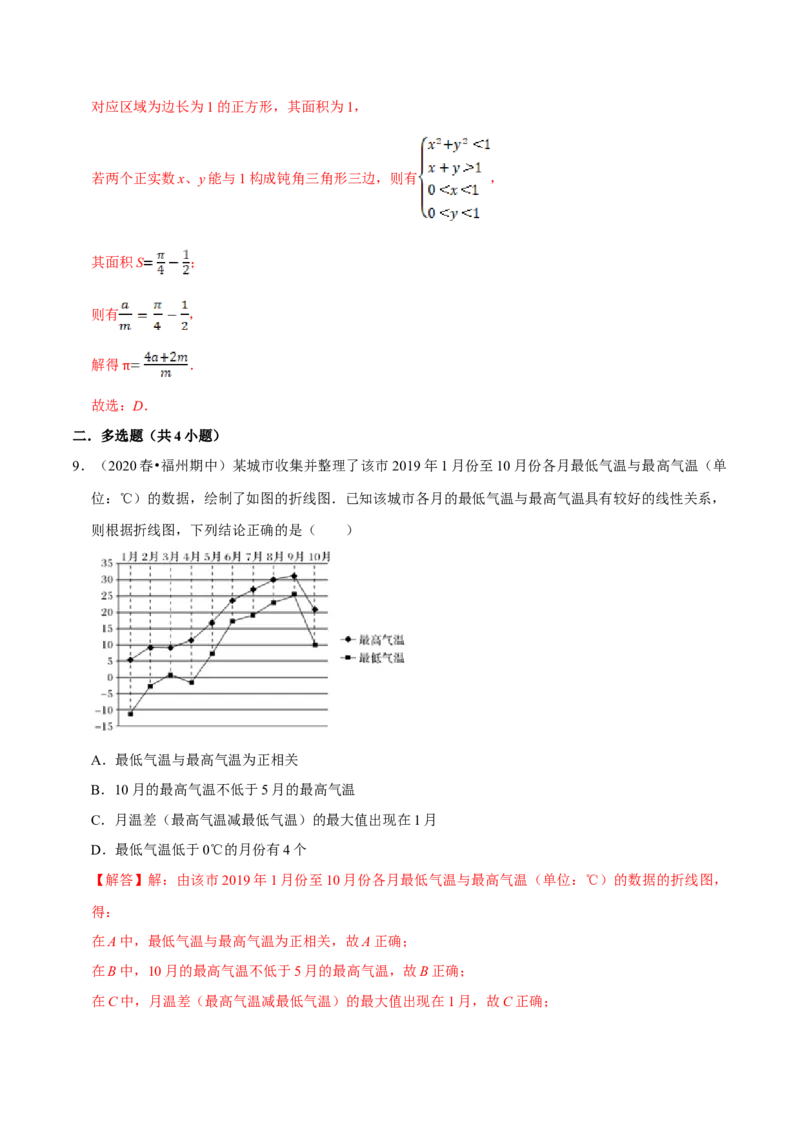
6.(2020•定远县模拟)我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学
联赛(河南初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生成绩的中位数是
81,乙班学生成绩的平均数是86,若正实数a,b满足a,G,b成等差数列且x,G,y成等比数列,则
的最小值为( )A. B.2 C. D.9
【解答】解:甲班学生成绩的中位数是80+x=81,得x=1;
由茎叶图可知乙班学生的总分为76+80×3+90×3+(0+2+y+1+3+6)=598+y,
乙班学生的平均分是86,且总分为86×7=602,所以y=4,
若正实数a、b满足:a,G,b成等差数列且x,G,y成等比数列,
则xy=G2,2G=a+b,即有a+b=4,a>0,b>0,
则 (a+b)( ) (1+4 ) (5+2 ) 9 ,
当且仅当b=2a 时, 的最小值为 .
故选:C.
7.(2020•松江区二模)已知实数x ,x ,……,x [﹣1,1],且x +x +……+x = ,则当x 2+x 2+……
1 2 100 1 2 100 1 2
+x 2取得最大值时,x ,x ,……,x 这100个数∈中,值为1的个数为( ) π
100 1 2 100
A.50个 B.51 个 C.52 个 D.53个
【解答】解:∵x +x +……+x = ,则当x 2+x 2+……+x 2要取得最大值,只需正负抵消,即有48个
1 2 100 1 2 100
﹣1,51个1,1个无理数为 ﹣3时π符合试题要求,
故选:B. π
8.(2020春•四川月考)关于圆周率 ,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和
查理斯实验.受其启发,我们也可以π通过设计下面的实验来估计 的值:先请全校m名同学每人随机写
下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角π 三形三边的数对(x,y)的个数a;
最后再根据统计数a估计 的值,那么可以估计 的值约为( )
π π
A. B. C. D.
【解答】解:根据题意知,m名同学取m对都小于l的正实数对(x,y),即 ,对应区域为边长为1的正方形,其面积为1,
若两个正实数x、y能与1构成钝角三角形三边,则有 ,
其面积S ;
则有 ,
解得 .
π
故选:D.
二.多选题(共4小题)
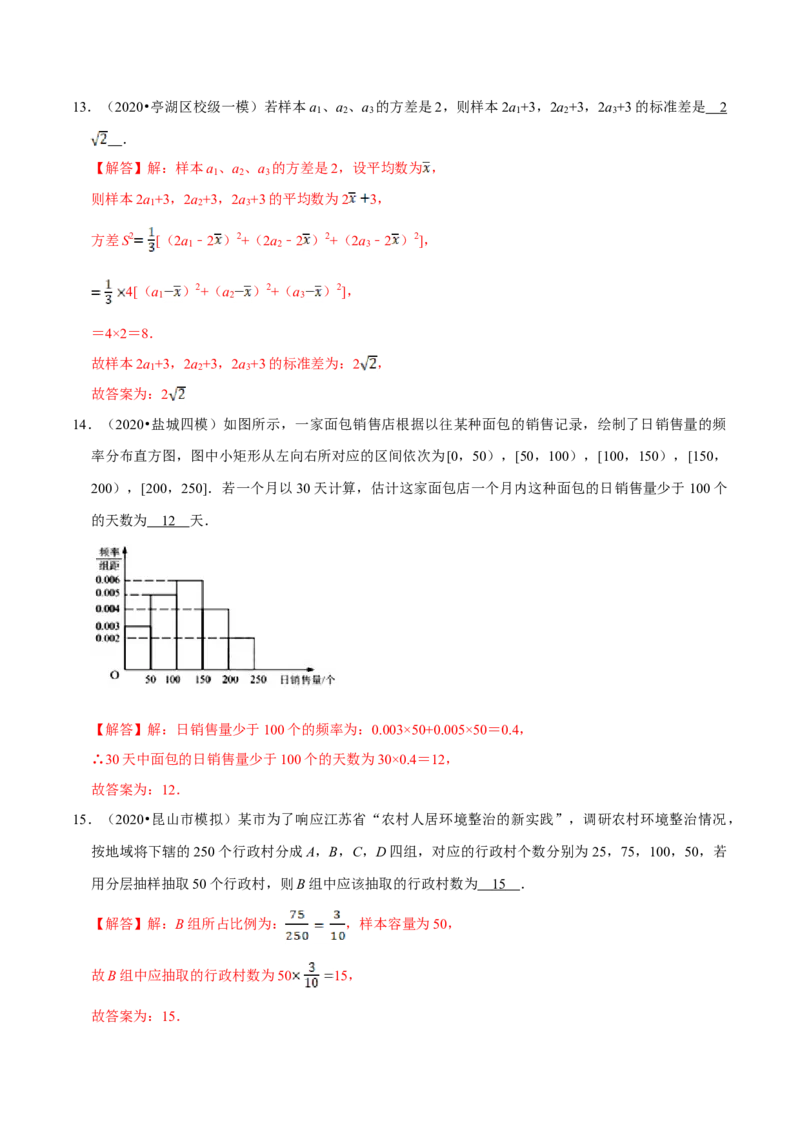
9.(2020春•福州期中)某城市收集并整理了该市2019年1月份至10月份各月最低气温与最高气温(单
位:℃)的数据,绘制了如图的折线图.已知该城市各月的最低气温与最高气温具有较好的线性关系,
则根据折线图,下列结论正确的是( )
A.最低气温与最高气温为正相关
B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月
D.最低气温低于0℃的月份有4个
【解答】解:由该市2019年1月份至10月份各月最低气温与最高气温(单位:℃)的数据的折线图,
得:
在A中,最低气温与最高气温为正相关,故A正确;
在B中,10月的最高气温不低于5月的最高气温,故B正确;
在C中,月温差(最高气温减最低气温)的最大值出现在1月,故C正确;在D中,最低气温低于0℃的月份有3个,故D错误.
故选:ABC.
10.(2020春•胶州市期中)在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大
规模群体感染的标志为“连续7天,每天新增疑似病例不超过5人”.过去7日,甲、乙、丙、丁四地
新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:总体平均数 ,且中位数为0;
乙地:总体平均数为2,且标准差s≤2;
丙地:总体平均数 ,且极差c≤2;
丁地:众数为1,且极差c≤4.
A.甲地 B.乙地 C.丙地 D.丁地
【解答】解:该事件在一段时间内没有发生大规模群体感染的标志为“连续7天,每天新增疑似病例不
超过5人”.
甲地:总体平均数 ,且中位数为0,
存在连续7天中某一天新增疑似病例超过5人的可能,故甲地不一定符合标准,故A错误.
乙地:总体平均数为2,且标准差s≤2,
存在连续7天中某一天新增疑似病例超过5人的可能,
例如7天中增增病例数为1,1,1,1,2,2,6,
满足总体平均数为2,且标准差s≤2,故乙地不一定符合标准,故B错误;
丙地:总体平均数 ,且极差c≤2,
每天新增疑似病例没有超过5人的可能,故丙地一定符合标准,故C正确;
丁地:众数为1,且极差c≤4.
每天新增疑似病例没有超过5人的可能,故丁地一定符合标准,故D正确.
故选:CD.
11.(2020•德州一模)某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好
地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱图:则下列结论正确的是( )
A.与 2016 年相比,2019 年一本达线人数有所增加
B.与 2016 年相比,2019 年二本达线人数增加了0.5 倍
C.与 2016年相比,2019 年艺体达线人数相同
D.与 2016 年相比,2019 年不上线的人数有所增加
【解答】解:依题意,设2016年高考考生人数为x,则2019年高考考生人数为1.5x,
由24%•1.5x﹣28%•x=8%•x>0,故选项A正确;
由(40%•1.5x﹣32%•x)÷32%•x ,故选项B不正确;
由8%•1.5x﹣8%•x=4%•x>0,故选项C不正确;
由28%•1.5x﹣32%•x=42%•x>0,故选项D正确.
故选:AD.
12.(2020•潍坊一模)如图是《2018年全国教育事业发展统计公报》中1949﹣2018年我国高中阶段在校
生数条形图和毛入学率的折线图,根据如图可知在1949﹣2018年( )
A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高
B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高
C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰
D.2018年高中阶段在校生数比2017年下降了约0.9%而毛入学率提高了0.5个百分点
【解答】解:由图可知,1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高,A对;
2016年我国高中阶段的在校生数和毛入学率降低,B错;
2015年我国高中阶段在毛入学率均达到了最高峰,C错;
2018年高中阶段在校生数比2017年下降了约0.9%而毛入学率提高了0.5个百分点,D对,
故选:AD.
三.填空题(共4小题)13.(2020•亭湖区校级一模)若样本a 、a 、a 的方差是2,则样本2a +3,2a +3,2a +3的标准差是 2
1 2 3 1 2 3
.
【解答】解:样本a 、a 、a 的方差是2,设平均数为 ,
1 2 3
则样本2a +3,2a +3,2a +3的平均数为2 3,
1 2 3
方差S2 [(2a ﹣2 )2+(2a ﹣2 )2+(2a ﹣2 )2],
1 2 3
4[(a )2+(a )2+(a )2],
1 2 3
=4×2=8.
故样本2a +3,2a +3,2a +3的标准差为:2 ,
1 2 3
故答案为:2
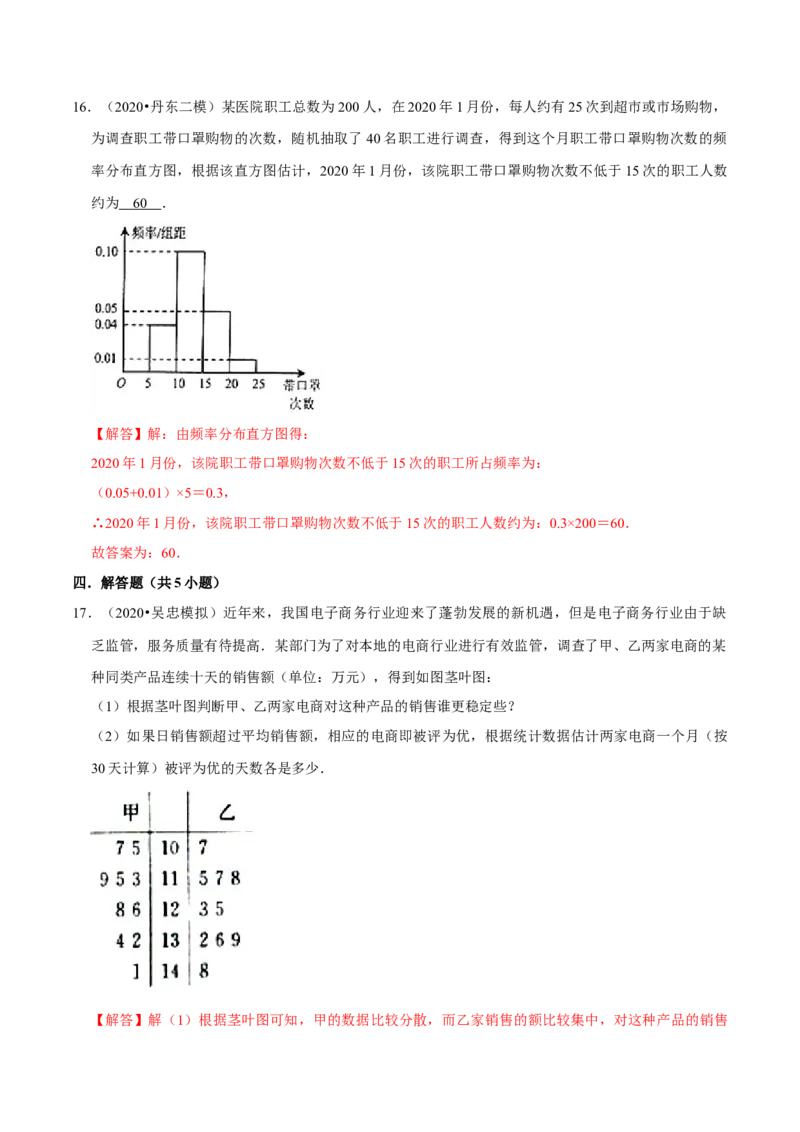
14.(2020•盐城四模)如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频
率分布直方图,图中小矩形从左向右所对应的区间依次为[0,50),[50,100),[100,150),[150,
200),[200,250].若一个月以30天计算,估计这家面包店一个月内这种面包的日销售量少于100个
的天数为 1 2 天.
【解答】解:日销售量少于100个的频率为:0.003×50+0.005×50=0.4,
∴30天中面包的日销售量少于100个的天数为30×0.4=12,
故答案为:12.
15.(2020•昆山市模拟)某市为了响应江苏省“农村人居环境整治的新实践”,调研农村环境整治情况,
按地域将下辖的250个行政村分成A,B,C,D四组,对应的行政村个数分别为25,75,100,50,若
用分层抽样抽取50个行政村,则B组中应该抽取的行政村数为 1 5 .
【解答】解:B组所占比例为: ,样本容量为50,
故B组中应抽取的行政村数为50 15,
故答案为:15.16.(2020•丹东二模)某医院职工总数为200人,在2020年1月份,每人约有25次到超市或市场购物,
为调查职工带口罩购物的次数,随机抽取了40名职工进行调查,得到这个月职工带口罩购物次数的频
率分布直方图,根据该直方图估计,2020年1月份,该院职工带口罩购物次数不低于15次的职工人数
约为 6 0 .
【解答】解:由频率分布直方图得:
2020年1月份,该院职工带口罩购物次数不低于15次的职工所占频率为:
(0.05+0.01)×5=0.3,
∴2020年1月份,该院职工带口罩购物次数不低于15次的职工人数约为:0.3×200=60.
故答案为:60.
四.解答题(共5小题)
17.(2020•吴忠模拟)近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺
乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某
种同类产品连续十天的销售额(单位:万元),得到如图茎叶图:
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)如果日销售额超过平均销售额,相应的电商即被评为优,根据统计数据估计两家电商一个月(按
30天计算)被评为优的天数各是多少.
【解答】解(1)根据茎叶图可知,甲的数据比较分散,而乙家销售的额比较集中,对这种产品的销售更稳定,
(2)甲的平均销售额 122,
故10天中甲的销售额超过平均值 122的有5天,从而30天中约有15天被评为优,
乙的销售额平均值 (107+115+117+118+123+125+132+136+139+148)=126,
10天中乙的销售额超过平均值 122的有4天,从而30天中约有12天被评为优,
18.(2020•临汾模拟)随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了
看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在 10~60
岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直
方图,如右图所示.
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在 40岁以上(含40
岁)的市民人数;
(2)若按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,再从这10
人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,求X的分布列以及
数学期望.
【解答】解:(1)由频率分布列知被调查的人员年龄在20~30岁间的市民的频率为0.030×10=0.3,
∵被调查的人员年龄在20~30岁间的市民有300人,
∴n 1000,
∵被调查人员的年龄在40岁以上(含40岁)的市民的频率为(0.020+0.005)×10=0.25,
∴被调查人员的年龄在40岁以上(含40岁)的市民人数为:0.25×1000=250人.
(2)年龄在[20,30)内的市民有:0.030×1000=300人,
年龄在[40,50)内的市民有:0.020×1000=200人,
按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,年龄在[20,30)内的市民抽中300 6人,
年龄在[40,50)内的市民抽中:200 4人,
再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,
则X的可能取值为0,1,2,3,
P(X=0) ,
P(X=1) ,
P(X=2) ,
P(X=3) ,
∴X的分布列为:
X 0 1 2 3
P
EX .
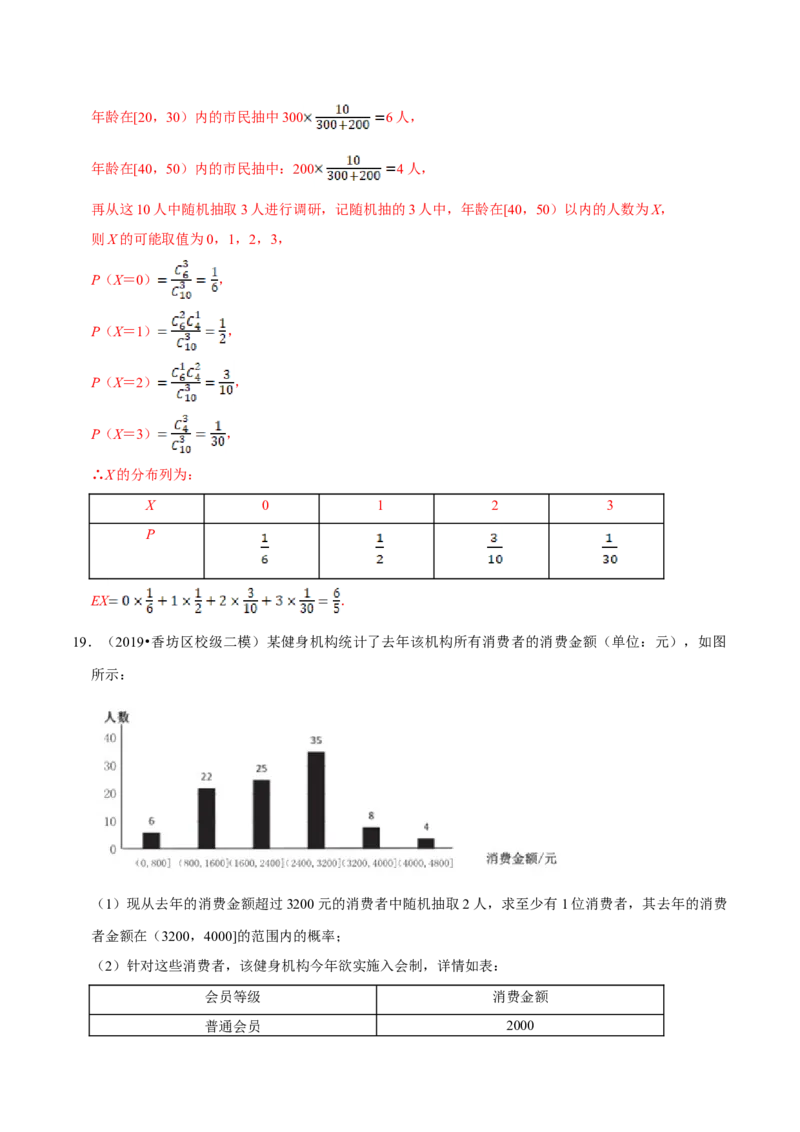
19.(2019•香坊区校级二模)某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如图
所示:
(1)现从去年的消费金额超过3200元的消费者中随机抽取2人,求至少有1位消费者,其去年的消费
者金额在(3200,4000]的范围内的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如表:
会员等级 消费金额
普通会员 2000银卡会员 2700
金卡会员 3200
预计去年消费金额在(0,1600]内的消费者今年都将会申请办理普通会员,消费金额在(1600,3200]
内的消费者都将会申请办理银卡会员,消费金额在(3200,4800]内的消费者都将会申请办理金卡会员,
消费者在申请办理会员时,需一次性缴清相应等级的消费金额,该健身机构在今年底将针对这些消费者
举办消费返利活动,现有如下两种预设方案:
方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励:
普通会员中的“幸运之星”每人奖励500元;银卡会员中的“幸运之星”每人奖励600元;金卡会员中
的“幸运之星”每人奖励800元.
方案二:每位会员均可参加摸奖游戏,游戏规则如下:从一个装有 3个白球、2个红球(球只有颜色不
同)的箱子中,有放回地摸三次球,每次只能摸一个球,若摸到红球的总数为 2,则可获得200元奖励
金;若摸到红球的总数为3,则可获得300元奖励金;其他情况不给予奖励.规定每位普通会员均可参
加1次摸奖游戏;每位银卡会员均可参加2次摸奖游戏;每位金卡会员均可参加3次摸奖游戏(每次摸
奖的结果相互独立)
请你预测哪一种返利活动方案该健身机构的投资较少?并说明理由.
【解答】解:(1)去年的消费金额超过3200元的消费者有12人,
其中去年的消费金额在(3200,4000]的消费者有8人,
去年的消费金额在(4000,4800]的消费者有4人,
现从去年的消费金额超过3200元的消费者中随机抽取2人,
基本事件总数n 66,
至少有1位消费者,其去年的消费者金额在(3200,4000]的范围内包含的基本事件个数:
m 38,
∴至少有1位消费者,其去年的消费者金额在(3200,4000]的范围内的概率为:
p .
(2)方案一:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励,
则“幸运之星”中的普通会员、银卡会员、金卡会员的人数分别为:
, , ,
∴根据方案一的奖励的金额为:=7×500+15×600+3×800=14900元,
1
ξ方案二:设 表示参加一次摸奖游戏所获的奖励金,
则 的可能取η值分别为0,200,300,
η
摸到红球的概率为P ,
P( =0) ,
η
P( =200) ,
η
P( =300) ,
η
的分布列为:
η 0 200 300
ηP
∴E 76.8元,
η
∴按照方案二奖励金的金额为:
=(28+2×60+3×12)×76.8=14131.2元,
2
ξ∵方案一奖励的总金额 >方案二的奖励金额 ,
1 2
∴预计方案二的投资较小ξ . ξ
20.(2020•江西模拟)冠状病毒是一个大型病毒家族,可引起感冒以及中东呼吸综合征(MERS)和严重
急性呼吸综合征(SARS)等较严重疾病.出现在湖北武汉的新型冠状病毒(nCoV)是从未在人体中发
现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难
等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状
病毒,需要检测血液中的指标A.现从采集的血液样品中抽取500份检测指标A的值,由测量结果得如
图频率分布直方图:
(1)求这500份血液样品指标A值的平均数 和样本方差s2(同一组数据用该区间的中点值作代表,记
作x(i=1,2,…,7));
i
(2)由频率分布直方图可以认为,这项指标A的值X服从正态分布N( ,σ2),其中 近似为样本平
均数 ,σ2近似为样本方差s2.在统计学中,把发生概率小于3‰的事件μ称为小概率事件μ(正常条件下
小概率事件的发生是不正常的).该医院非常关注本院医生健康状况,随机抽取 20名医生,独立的检测血液中指标A的值,结果发现4名医生血液中指标A的值大于正常值20.03,试根据题中条件判断该
院医生的健康率是否正常,并说明理由.
附:参考数据与公式: ,3.46 ;若x~N( ,σ2),则 P( ﹣σ<
μ ① μ
x≤ +σ ) = 0.6826 ; P ( ﹣ 2σ < x≤ +2σ ) = 0.9545 ; P ( ﹣ 3σ < x≤ +3σ ) =
0.99μ73.0.15874≈0.006,0②.15876≈0μ.000016,0.84μ1314≈0.0890,0.84131③6≈0.0630μ. μ
【 解 答 】 解 : ( 1 )
,
.
(2)由题意知:X~N(17.4,6.92),20.03= +σ,
μ
.
随机抽取20名医生独立检测血液中指标A的值,就相当于进行了20次独立重复试验,
记“20名医生中出现4名医生血液中指标A的值大于正常值20.03”为事件B,
则
=4845×0.0006×0.0630=0.183141>3%,
所以从血液中指标A的值的角度来看:该院医生的健康率是正常的.
21.(2019秋•河南月考)某社区100名居民参加2019年国庆活动,他们的年龄在30岁至80岁之间,将
年龄按[30,40),[40,50),[50,60),[60,70),[70,80]分组,得到的频率分布直方图如图所示:
(1)求a的值,并求该社区参加2019年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在[50,60),[70,80]的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3
人进行座谈,用X表示参与座谈的居民的年龄在[70,80]的人数,求X的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地30岁至80岁之间的市民中抽取20名进行调
查,其中有k名市民的年龄在[30,50)的概率为P (k=0,1,2,…,20),当P 最大时,求k的值.
k k【解答】解:(1)由频率分布直方图得:
(0.005+0.010+0.030+0.035)×10=1,
解得a=0.02,
∴该社区参加2019年国庆活动的居民的平均年龄为:
(0.005×35+0.035×45+0.030×55+0.020×65+0.010×75)×10=54.5.
(2)年龄在[50,60)的人数为0.030×10×100=30,
年龄在[70,80)的人数为0.010×10×100=10,
根据分层抽样,可知年龄在[50,60)的抽取6人,年龄在[70,80)的抽取2人,
∴X的可能取值为0,1,2,
P(X=0) ,
P(X=1) ,
P(X=2) ,
∴X的分布列为:
X 0 1 2
P
∴数学期望E(X) .
(3)设在抽取的20名市民中,年龄在[30,50)内的人数为Y,则Y服从二项分布,
由频率分布直方图得年龄在[30,50)的频率为:(0.005+0.035)×10=0.4,
∴Y~B(20,0.4),
∴P(Y=k) ,(k=0,1,2,…,20),
设t ,当t>1时,k<8.4,P(Y=k﹣1)<P(Y=k),
当t<1时,k>8.4,P(Y=k﹣1)>P(Y=k),
∴当k=8时,P(Y=k)最大,即当P(Y=k)最大时,k=8.