江苏省百校联考2024-2025学年高一下学期5月月考试题数学PDF版含答案_2024-2025高一（7-7月题库）_2025年6月7.10新增_0609江苏省百校联考2024-2025学年高一下学期5月月考试题

江苏省 2024-2025 学年高一下学期百校联考数学试卷
一、单项选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只
有一项是符合题目要求的。
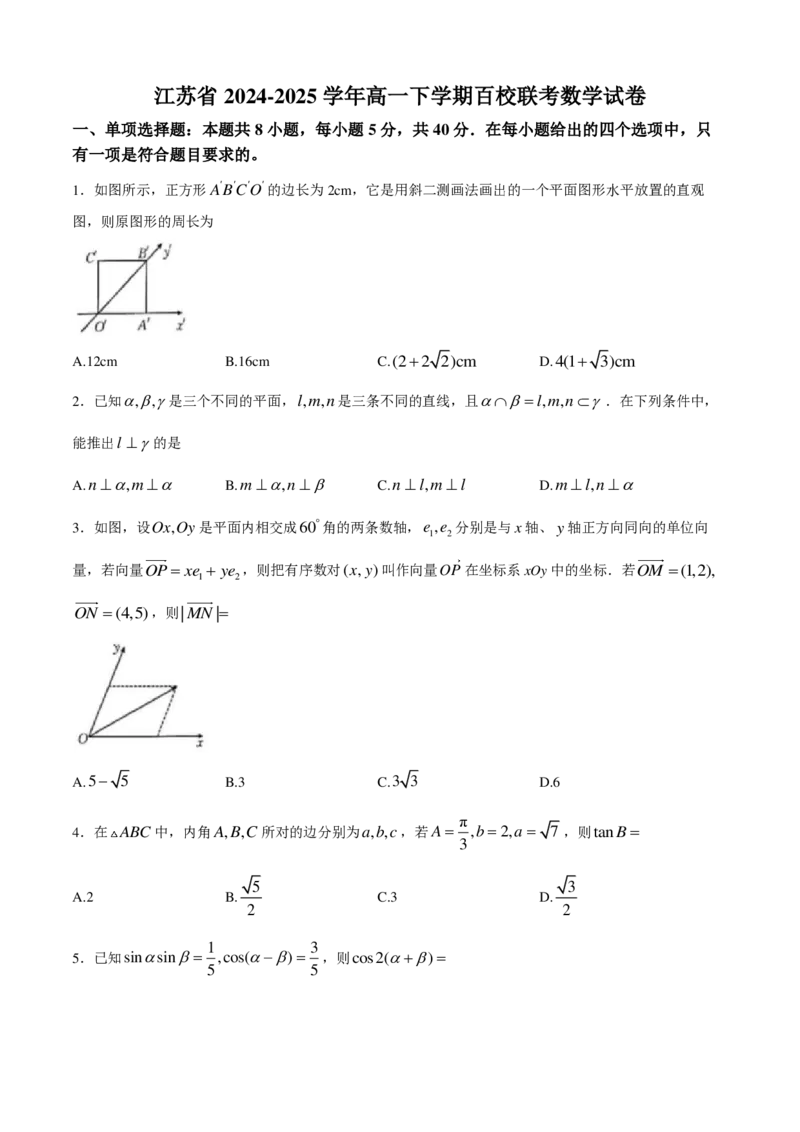
1．如图所示，正方形 A B C O  的边长为2cm，它是用斜二测画法画出的一个平面图形水平放置的直观
图，则原图形的周长为
A.12cm B.16cm C.(22 2)cm D.4(1 3)cm
2．已知 , , 是三个不同的平面， l , m , n 是三条不同的直线，且 l , m , n       ．在下列条件中，
能推出 l   的是
A. n , m     B. m , n     C. n  l , m  l D.ml,n
3．如图，设 O x , O y 是平面内相交成 6 0  角的两条数轴， e
1
, e
2
分别是与x轴、 y 轴正方向同向的单位向
量，若向量 O P  x e
1
 y e
2
，则把有序数对 ( x , y ) 叫作向量OP在坐标系xOy中的坐标．若
O N  ( 4 , 5 )
O M  ( 1 , 2 ) ,
，则 | M N |
A.5 5 B.3 C. 3 3 D.6
4．在 A B C 中，内角 A , B , C 所对的边分别为a,b,c，若 A 
π
3
, b  2 , a  7 ，则 t a n B 
5 3
A.2 B. C.3 D.
2 2
1 3
5．已知sinsin ,cos() ，则
5 5
c o s 2 ( )    A. 
1
5
B.
1
5
C.
1
2
8
5
23
D.
25
6．在三棱锥PABC中，PB  PC  AB  AC  BC 4,PA2 3，则异面直线PB与AC所成角的
正切值是
A. 
1
2
5
B.
1
2
5
C.3 7 D.3 7
7．如图，在 A B C D 中，  D A B  6 0  , A B  2 A D , E 为边AB的中点，线段AC与DE交于点 F ，则
cosAFE 
A. 
3
1
2
4
1 21
B. C.
7

1
7
4
1
D.
7
8．在 A B C 中， a , b , c 分别为内角 A , B , C 所对的边，已知 a c o s C  3 a s i n C  b  c  0 ．设 D 为边
BD 2c
BC上一点，若AD  7，且  ，则 ABC面积的最小值为
CD b
A. 2 3 B.3 3 C. 4 3 D.6 3
二、多项选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的四个选项中，有
多项符合题目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分．
9．已知正方体 A B C D  A
1
B C1
1
D
1
的棱长为1，点P在线段BD上运动，则
A. C
1
P  A C1 B.直线 B
1
P 一定与 A D
1
共面
C. S
A C1 P
3
的最小值为 D.
4
A P  C
1
P 的最小值为
6 
2
2
10．在 ABC中，内角A,B,C所对的边分别为a,b,c，且a2 b2 c2 bc0，则下列说法正确的是
π
A.A B.若a 4，则
4
A B C 面积的最大值为4 3
4 4 33
C.若a  3,cosB  ，则c D.若
5 5
b s i n C  s i n C  3 c o s C ，则c2
11．已知函数 f(x)(xD)，若存在非零常数T,xD，都有 f(xT) f(x)成立，我们就称 f(x)为“T 不减函数”，若  x  D ，都有 f(xT) f(x)成立，我们就称 f ( x ) 为“严格 T 增函数”．下列说法正
确的是
A.函数 f(x)cosxsinx(DR)是“ T 不减函数”
B.若函数g(x)asinxbcosx(ab0)，则g(x)一定不是“严格T 增函数”
C.函数 f ( x )  2 s i n

2 x 
π
6

( D  [ 0 , π ] ) 为“严格 
π
6
增函数”
D.若函数 f ( x )  k x  s i n 2 x ( D  R ) 是“
π
2
不减函数”，则 k 的取值范围为
 2
π
,  

三、填空题：本题共 3小题，每小题 5分，共 15 分．
12．若两个单位向量 a , b 满足 | a  b | 3 | a  b | ，则a与 b 的夹角是__________．
13．已知 3 s i n c o s 2 0 , s i n 2 s i n ( )           ，则 t a n ( )     __________．
14．在锐角 A B C 中，a,b,c分别是内角 A , B , C 的对边，bsinAatanAcosB 3asinC,AD
2 1
 AB AC且
3 3
A B C 的面积为3，过点D分别作 D M  A B 于点 M , D N  A C 于点 N ，则
D M  D N  __________.
四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题13分）已知平面向量 a , b 满足 | a | 2 2 , | b | 2 ，且 | a  2 b | 2 1 0 ．
（1）求 a 在b方向上的投影向量；
（2）若 ( a b ) ( 2 a b )     ，求实数的值．
16．（本小题15分）如图，在长方体 A B C D  A
1
B C1
1
D
1
中，底面ABCD是边长为4的正方形， O 为AC
与BD的交点， B B
1
 2 2 , M 是线段 B
1
D
1
的中点．
（1）求证： B M / / 平面 D
1
A C ．
（2）求证：DO 平面ABC．
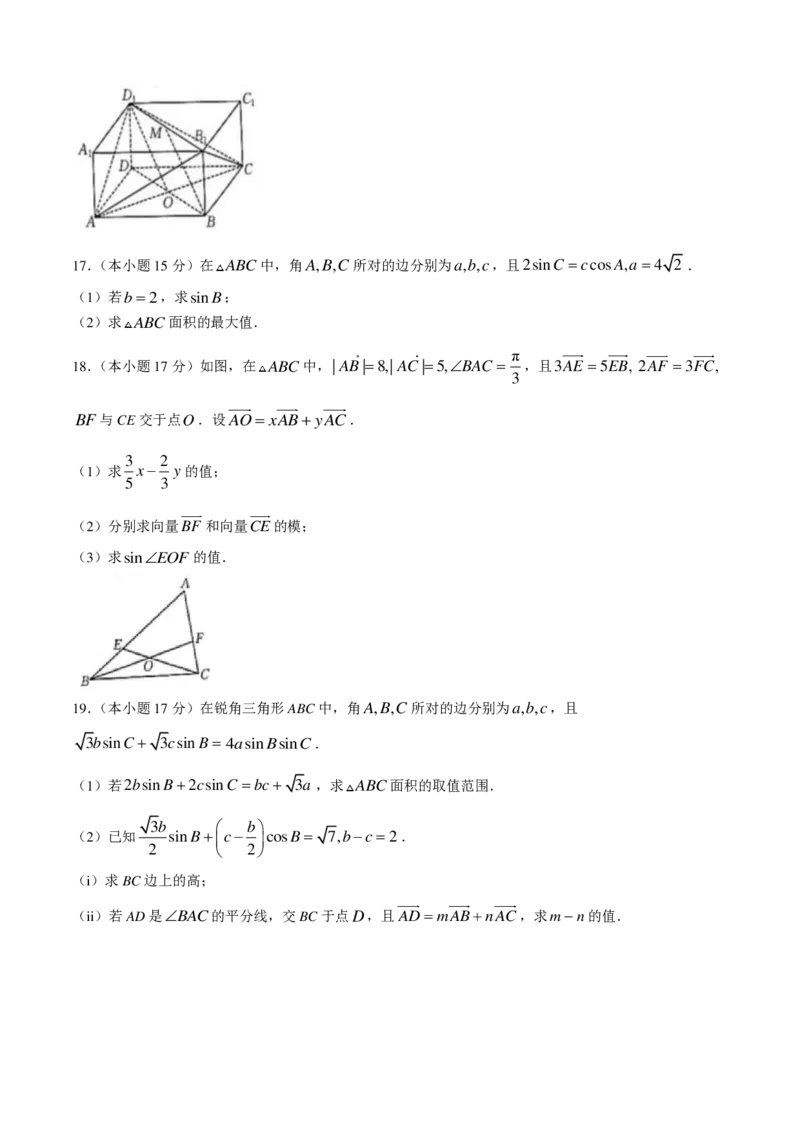
1 117．（本小题15分）在 A B C 中，角 A , B , C 所对的边分别为 a , b , c ，且 2 s i n C  c c o s A , a  4 2 ．
（1）若 b  2 ，求 s i n B ；
（2）求 A B C 面积的最大值．
18．（本小题17分）如图，在 A B C 中， | A B | 8 , | A C | 5 ,  B A C 
π
3
，且3AE 5EB,
B F
2 A F  3 F C ,
与CE交于点 O ．设 A O  x A B  y A C ．
（1）求
3
5
x 
2
3
y 的值；
（2）分别求向量 B F 和向量 C E 的模；
（3）求 s i n  E O F 的值．
19．（本小题17分）在锐角三角形ABC中，角 A , B , C 所对的边分别为 a , b , c ，且
3bsinC 3csinB  4 a s i n B s i n C ．
（1）若 2 b s i n B  2 c s i n C  b c  3 a ，求 A B C 面积的取值范围．
（2）已知
3
2
b
s i n B 

c 
b
2

c o s B  7 , b  c  2 ．
（i）求BC边上的高；
（ii）若AD是  B A C 的平分线，交BC于点D，且ADmABnAC，求mn的值．参考答案
1．B 2．B 3．C 4．D 5．D 6．C 7．C 8．A 9．AD 10．BD 11．ABD
12．
π
3
1 8 2
13． 14．
3 27
15．解：（1）由 | a | 2 2 , | b | 2 ，且 | a  2 b | 2 1 0 ，
两边平方得 | a 2|  4 a  b  4 | b 2|  8  4 a  b  1 6  4 0 ，解得ab4，．．．．．．．．．．．．．．．．．．．．．．．3分
b ab b ab
所以a在b方向上的投影向量为|a|cos    bb．．．．．．．．．．．．．．．．．．．．．．6分
|b| |b| |b| |b|2
（2）因为 ( a b ) ( 2 a b ) ,  +  - 所以 ( a b ) ( 2 a b ) 0 ,  +  -  ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分
化简得 2 a
2
 2 1  a b b
2
0 ,        ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分
所以 1 6 4 ( 2 1 ) 4 0 ,       ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分
解得 3    ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．13分
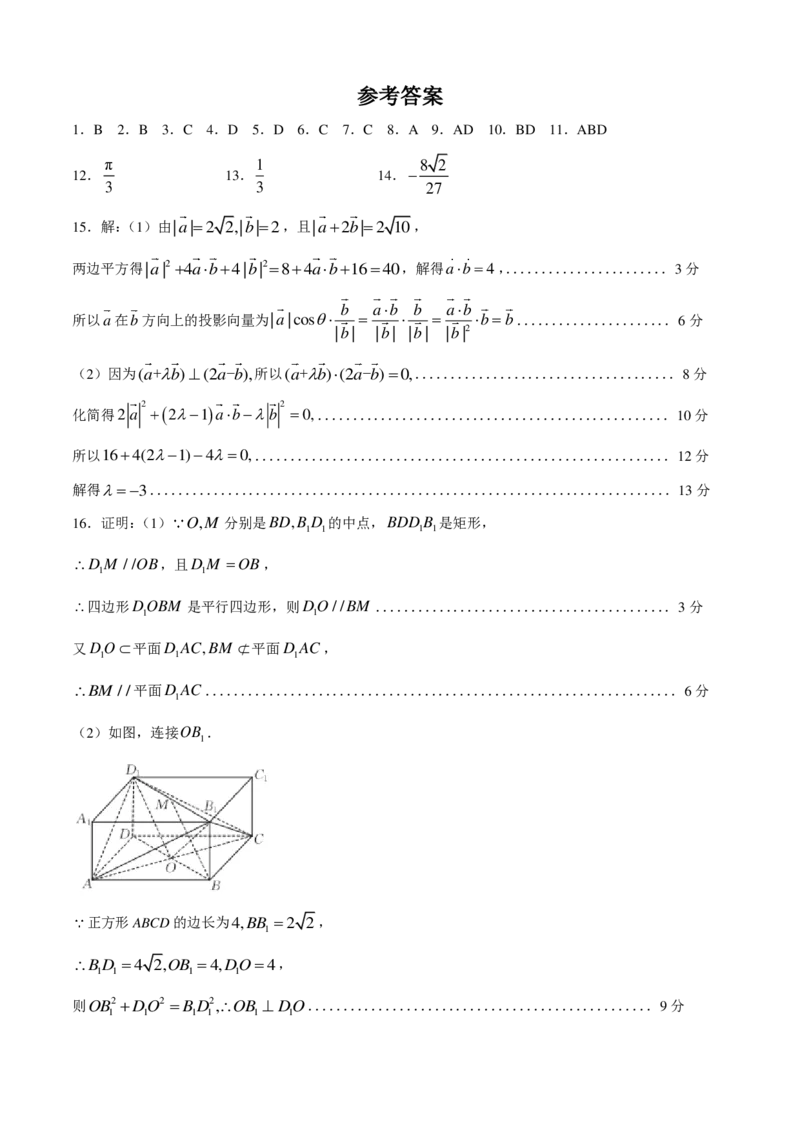
16．证明：（1） O , M 分别是BD,BD 的中点，
1 1
B D D
1
B
1
是矩形，
DM //OB，且DM OB，
1 1
四边形 D O1 B M 是平行四边形，则 D O1 / / B M ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
又 D O1  平面 D
1
A C , B M  平面 D
1
A C ，
BM //平面 D
1
A C ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分
（2）如图，连接OB ．
1
正方形ABCD的边长为4,BB 2 2，
1
BD 4 2,OB 4,DO4，
1 1 1 1
则OB2 DO2 BD2,OB DO．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．9分
1 1 1 1 1 1又 D
1
D  平面 A B C D , A C  平面ABCD，
AC  DD.
1
由底面ABCD为正方形可得 A C  B D ，
又 D
1
D  B D  D , D
1
D  平面 B D D
1
B
1
, B D  平面 B D D
1
B
1
，
AC平面 B D D
1
B
1
．
又 DO 平面BDDB ，
1 1 1
 A C  D O1 ，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．13分
又ACOB O,AC 平面ABC,OB 平面
1 1 1
A B
1
C ，
 D O1  平面ABC．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．15分
1
a b c
17．解：（1）（方法一）由正弦定理   和已知可得
sinA sinB sinC s i
c
n C

c o
2
s A

s i
a
n A

4
s i n
2
A
，化
简可得sinA2 2cosA．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
又 s i n 2 A  c o s 2 A  1 , s i n A 
2
3
2
，
 s i n B 
b
a
s i n A 
4
2
2

2
3
2

1
3
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．7分
a b c ccosA csinB
（方法二）由正弦定理   及已知可得sinC   ,asinB 
sinA sinB sinC 2 b
bsinA．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
又 a  4 2 , b  2 ,
 c
4
s i n
2
2
B
s i n

B
c

c o
2
2
s
s
A
i n
,
A ,
即
 s
2
i n B
2 s

i n
c o
B
s

A ,
s i n A ,
1
两式平方相加可得sinB  ．
3
故当 b  2
1
时，sinB  ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．7分
3
（2）由已知可得asinC 2 2ccosAcsinA，化简可得tanA2 2 ，即 s i n A 
2
3
2
, c o s A 
1
3
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分
由余弦定理得 c o s A 
b 2 
2
c
b
2
c
 a 2

1
3
，得 b 2  c 2  3 2 
2
3
b c 2 b c ，
1 2
bc 24,S  bcsinA bc 8 2 ，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．13分
ABC 2 3
当且仅当 b  c  2 6 时， A B C 的面积取得最大值 8 2 ．
故 A B C 的面积最大值为 8 2 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．15分
18．解：（1）由 5 F C  3 F C  2 F C  2 A F  2 F C  2 A C , 8 E B  5 E B  3 E B  3 A E  3 E B  3 A B ，
2 3
知FC  AC,EB  AB，
5 8
所以 A O  x A B 
5
3
y A F 
8
5
x A E  y A C ．
又B,O,F 三点共线，所以 x 
5
3
y  1 ，同理可得
8
5
x  y  1 ，
所以
3
5
x 
2
3
y  0 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分
2 2 3
（2）BF  BC AC  AC AB AC  AC AB，
5 5 5
C E  C B  E B  C B 
3
8
A B  A B  A C 
3
8
A B 
5
8
A B  A C .．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分
| B F 2| 
 3
5
A C  A B

2

9
2 5
A C
2
 A B
2

6
5
A B  A C 
9
2 5
 5 2  8 2 
6
5
 2 0  4 9 ，
所以 | B F | 7 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分
2
5  2 25 2 5 25 5
|CE|2

AB AC

 AC  AB  ABAC 52  82  2025，
8  64 4 64 4
所以|CE|5．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分
3  5  3  5 2 3 2 11
（3）BFCE 

ACAB



AB AC



1

ABAC AB  AC 
5  8  8  8 5 8 2 0 
5
8
 8 2 
3
5
 5 2  
5
2
5
，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．14分
55 55
 
BFCE 11
2 2
所以cosEOF cosBF,CE     ，．．．．．．．．．．．．．．．．．．．．．．．．16分
|BF ||CE| 75 35 14
所以 s i n  E O F 
5
1 4
3
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．17分
19．解：（1）由 3 b s i n C  3 c s i n B  4 a s i n B s i n C 及正弦定理，
得 3 s i n B s i n C  3 s i n C s i n B  4 s i n A s i n B s i n C ．
因为 0  B 
π
2
, 0  C 
π
2
，所以 s i n B  0 , s i n C  0 ，
所以 s i n A 
2
3
，又 0  A 
π
2
π
，所以A ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
3
由正弦定理得
s i
b
n B

s i
c
n C

s i
a
n A

2
3
3
a , s i n B 
2
3
a
b
, s i n C 
2
3
a
c
．
由 2 b s i n B  2 c s i n C  b c  3 a ，得 2 b
2
3
a
b
 2 c
2
3
a
c
 b c  3 a ，
即 b 2  c 2  a 2 
3
3
a b c ．由余弦定理得 b 2  c 2  a 2  b c ，解得a  3，．．．．．．．．．．．．．．．．．．5分
所以 b  2 s i n B , c  2 s i n C ，
S
A B C

1
2
b c s i n A  3 s i n B s i n C  3 s i n B s i n
 2 π
3
 B


2
3
s i n

2 B 
π
6


4
3
. ．．．．．．．．．7分
因为 A B C
π
为锐角三角形，所以0 B 且
2
B 
π
3

π
2
，
π π π π 5π
即  B ，所以 2B  ，
6 2 6 6 6
1  π
所以 sin  2B  1，所以
2  6 2
3
 S
A B C
3
4
3
．
 3 3 3
故 ABC面积的取值范围为 , ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．9分
2 4
 （2）（i）因为
3
2
b
s i n B 

c 
b
2

c o s B  7 ，所以 c c o s B  b c o s

B 
π
3

 7 ，
而 A 
π
3
，即 c c o s B  b c o s C  7 ，所以 2 R ( s i n C c o s B  s i n B c o s C )  7 ，
其中 R 为 A B C 外接圆的半径，所以 2 R s i n A  7 ，即a  7，．．．．．．．．．．．．．．．．．．．．．．．．．．．11分
所以 7  b 2  c 2  2 b c c o s A  b 2  c 2  b c  ( b  c ) 2  b c ，
则 b c  3 ，所以 S
A B C

1
2
b c s i n A 
3
4
3

1
2
 7  h ，
其中 h 为BC边上的高，故 h 
3
1
2
4
1
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．13分
（ii）由上面可以解出b3,c1,AD是  B A C 的平分线，
应用正弦定理可证 B D : D C  A B : A C  1 : 3 ，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．15分
则 A D 
3
4
A B 
1
4
A C ，所以 m  n 的值为
1
2
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．17分