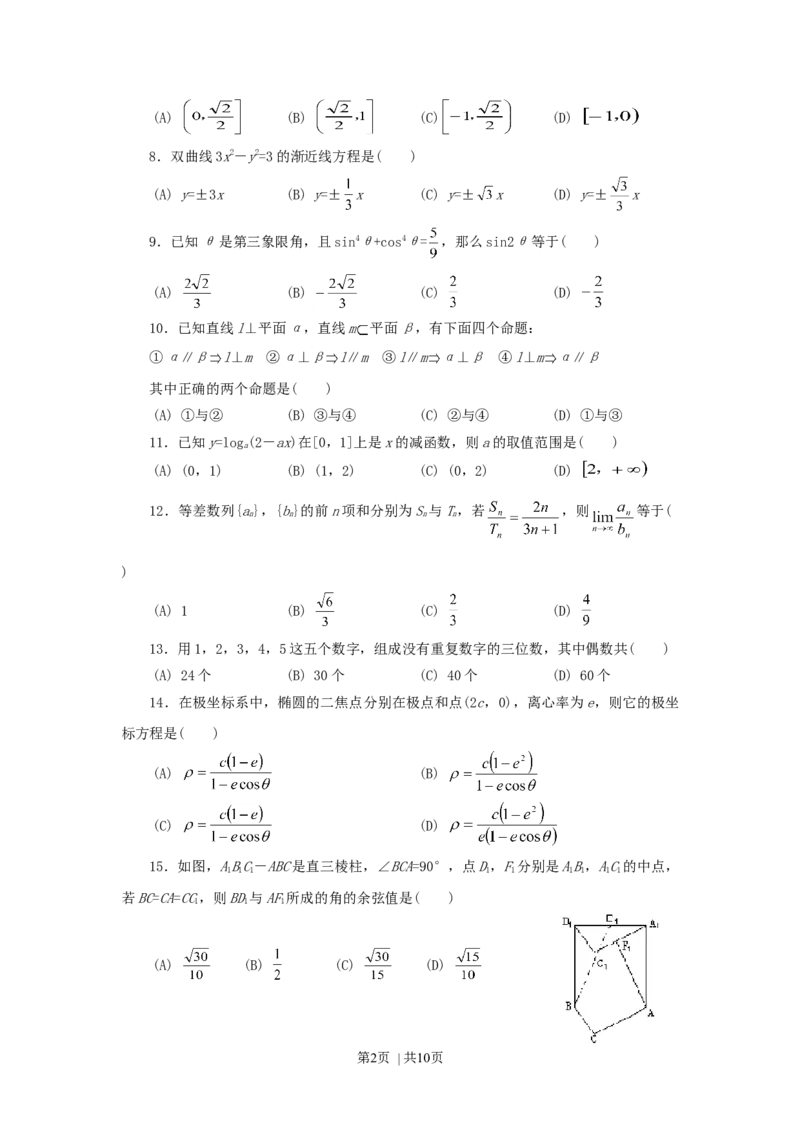文档内容
1995 年吉林高考理科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分.
第Ⅰ卷(选择题共65分)
一、选择题(本大题共15小题,第1—10题每小题4分,第11—15题每小题5分,共65分.
在每小题给出的四个选项中,只有一项是符合题目要求的)
王新奎新疆屯敞
1.已知I为全集,集合M,N I,若M∩N=N,则( )
(A) (B) (C) (D)
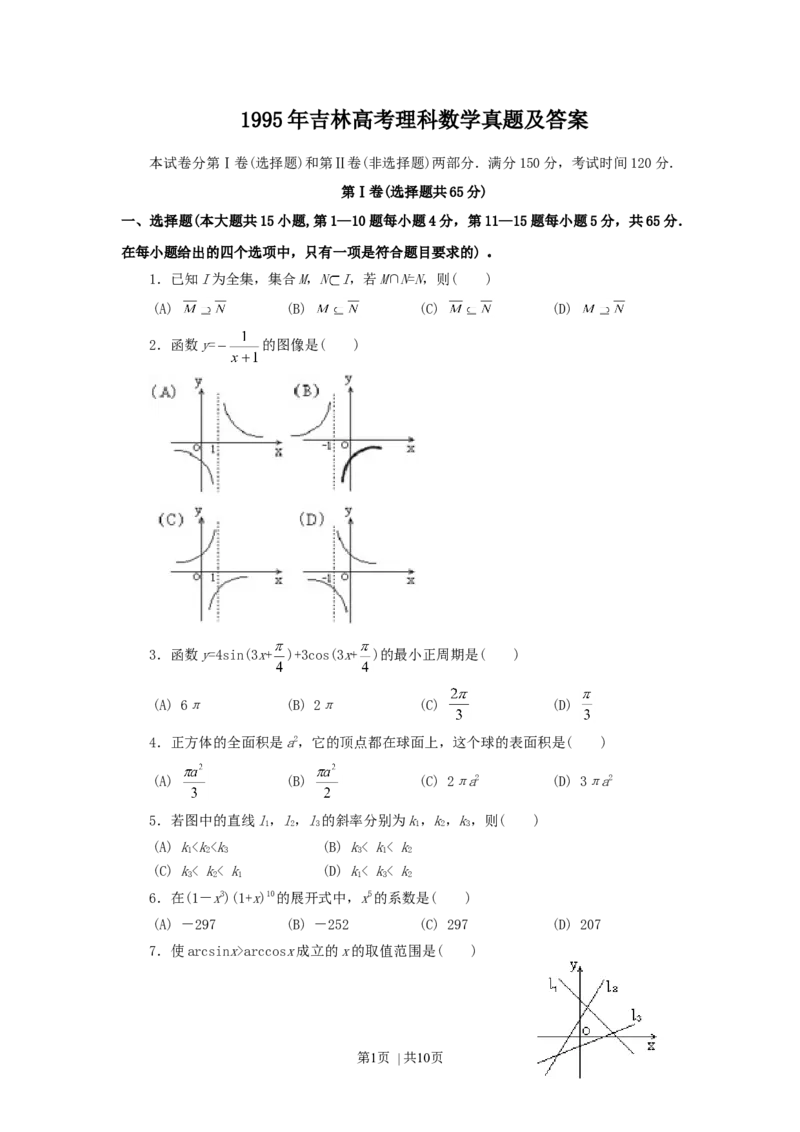
2.函数y= 的图像是( )
3.函数y=4sin(3x+ )+3cos(3x+ )的最小正周期是( )
(A) 6π (B) 2π (C) (D)
4.正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是( )
(A) (B) (C) 2πa2 (D) 3πa2
5.若图中的直线l,l,l的斜率分别为k,k,k,则( )
1 2 3 1 2 3
(A) karccosx成立的x的取值范围是( )
第1页 | 共10页(A) (B) (C) (D)
8.双曲线3x2-y2=3的渐近线方程是( )
(A) y=±3x (B) y=± x (C) y=± x (D) y=± x
9.已知θ是第三象限角,且sin4θ+cos4θ= ,那么sin2θ等于( )
(A) (B) (C) (D)
10.已知直线l⊥平面α,直线m 平面β,有下面四个命题:
①α∥β l⊥m ②α⊥β l∥m ③l∥m α⊥β ④l⊥m α∥β
其中正确的两个命题是( )
(A) ①与② (B) ③与④ (C) ②与④ (D) ①与③
11.已知y=log(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
a
(A) (0,1) (B) (1,2) (C) (0,2) (D)
12.等差数列{a},{b}的前n项和分别为S与T,若 ,则 等于(
n n n n
)
(A) 1 (B) (C) (D)
13.用1,2,3,4,5这五个数字,组成没有重复数字的三位数,其中偶数共( )
(A) 24个 (B) 30个 (C) 40个 (D) 60个
14.在极坐标系中,椭圆的二焦点分别在极点和点(2c,0),离心率为e,则它的极坐
标方程是( )
(A) (B)
(C) (D)
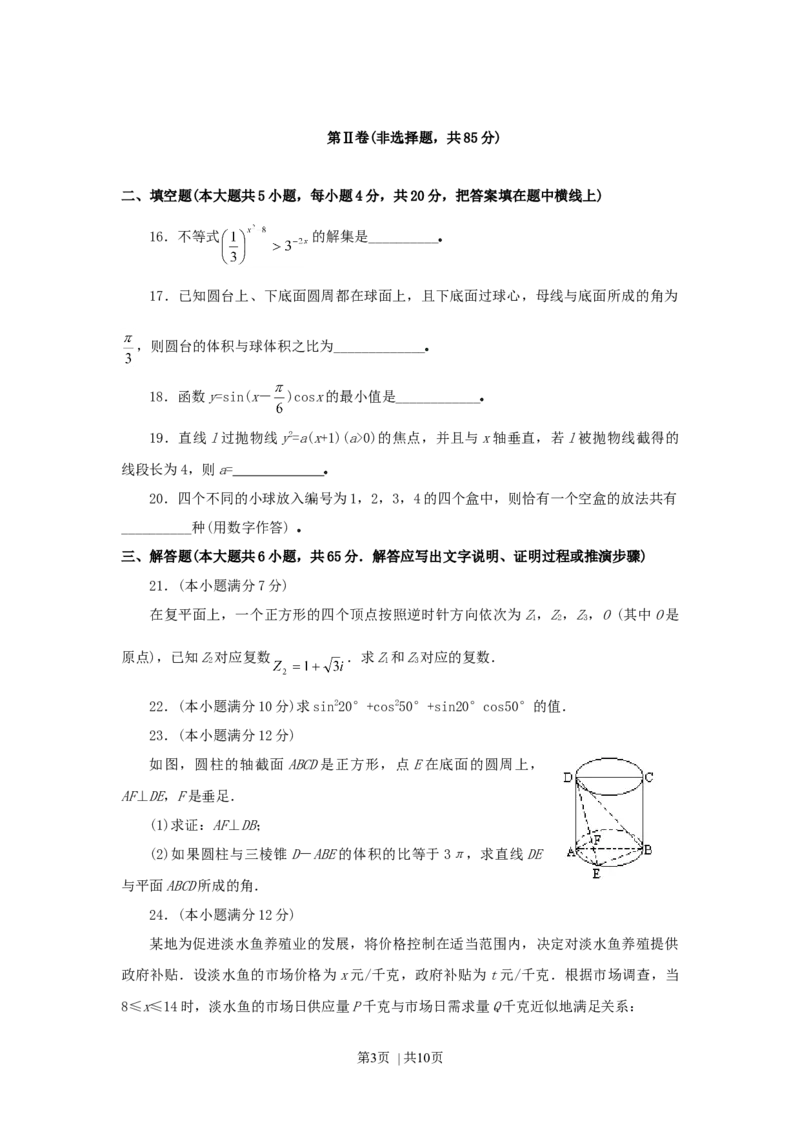
15.如图,ABC-ABC是直三棱柱,∠BCA=90°,点D,F分别是AB,AC的中点,
1 1 1 1 1 1 1 1 1
若BC=CA=CC,则BD与AF所成的角的余弦值是( )
1 1 1
(A) (B) (C) (D)
第2页 | 共10页第Ⅱ卷(非选择题,共85分)
二、填空题(本大题共5小题,每小题4分,共20分,把答案填在题中横线上)
16.不等式 的解集是__________
王新奎新疆屯敞
17.已知圆台上、下底面圆周都在球面上,且下底面过球心,母线与底面所成的角为
,则圆台的体积与球体积之比为_____________
王新奎新疆屯敞
18.函数y=sin(x- )cosx的最小值是____________
王新奎新疆屯敞
19.直线l过抛物线y2=a(x+1)(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的
线段长为4,则a=
王新奎新疆屯敞
20.四个不同的小球放入编号为1,2,3,4的四个盒中,则恰有一个空盒的放法共有
__________种(用数字作答)
王新奎新疆屯敞
三、解答题(本大题共6小题,共65分.解答应写出文字说明、证明过程或推演步骤)
21.(本小题满分7分)
在复平面上,一个正方形的四个顶点按照逆时针方向依次为Z,Z,Z,O (其中O是
1 2 3
原点),已知Z对应复数 .求Z和Z对应的复数.
2 1 3
22.(本小题满分10分)求sin220°+cos250°+sin20°cos50°的值.
23.(本小题满分12分)
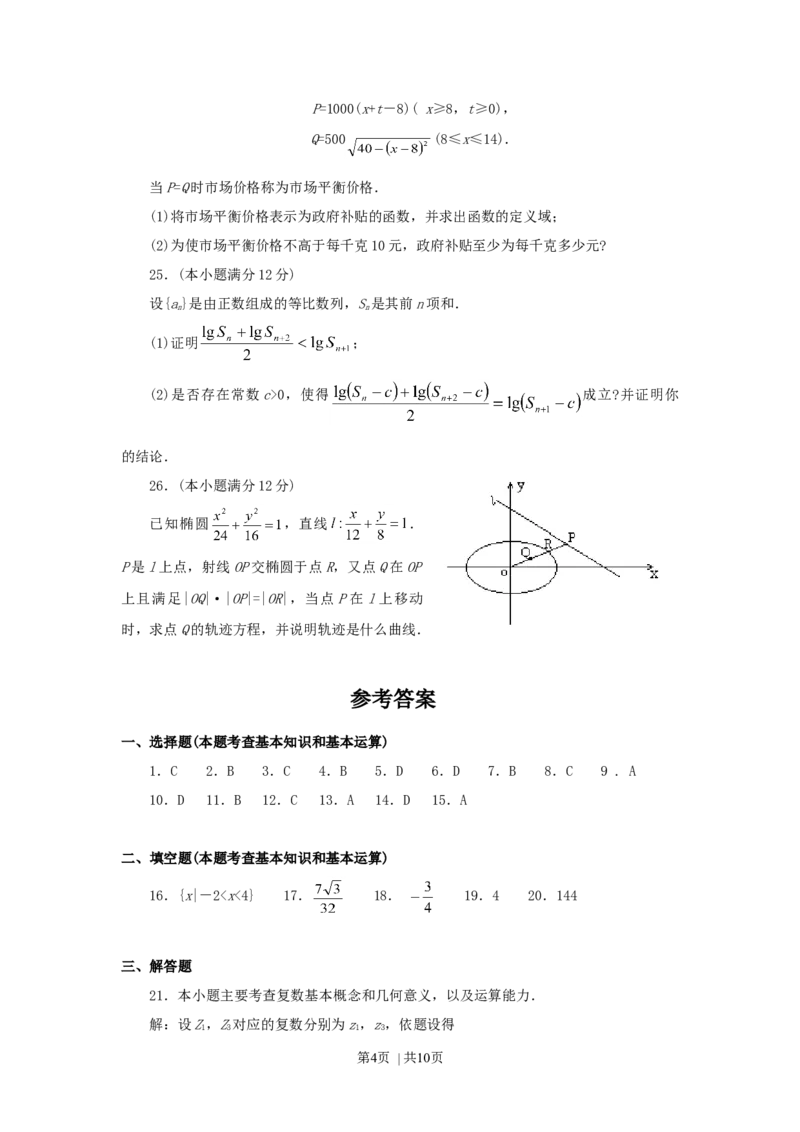
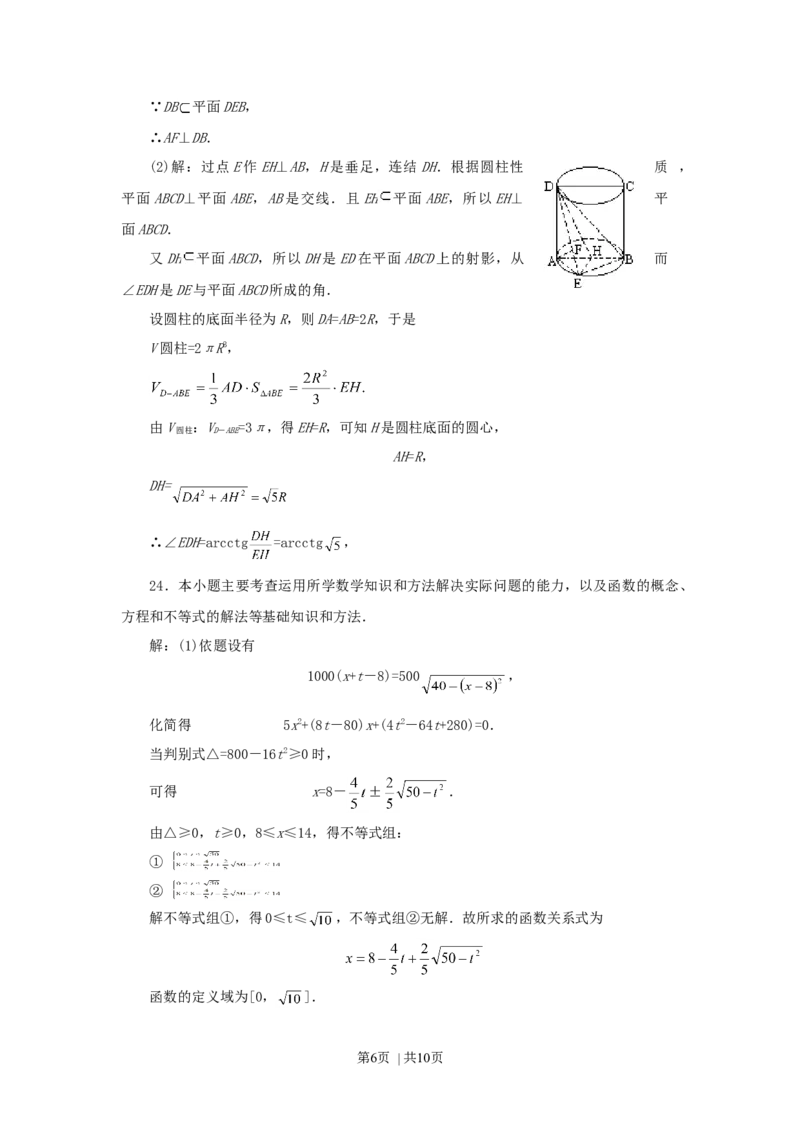
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,
AF⊥DE,F是垂足.
(1)求证:AF⊥DB;
(2)如果圆柱与三棱锥D-ABE的体积的比等于3π,求直线DE
与平面ABCD所成的角.
24.(本小题满分12分)
某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供
政府补贴.设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克.根据市场调查,当
8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系:
第3页 | 共10页P=1000(x+t-8)( x≥8,t≥0),
Q=500 (8≤x≤14).
当P=Q时市场价格称为市场平衡价格.
(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
25.(本小题满分12分)
设{a}是由正数组成的等比数列,S是其前n项和.
n n
(1)证明 ;
(2)是否存在常数c>0,使得 成立?并证明你
的结论.
26.(本小题满分12分)
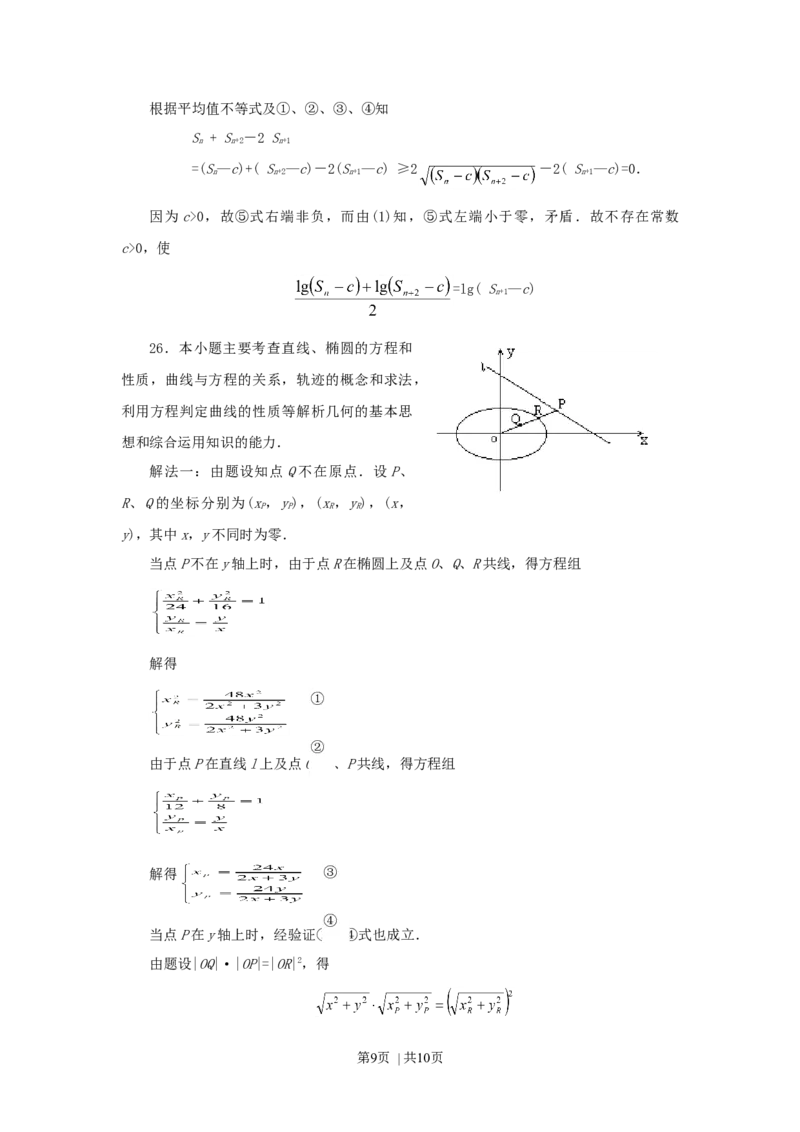
已知椭圆 ,直线 .
P是l上点,射线OP交椭圆于点R,又点Q在OP
上且满足|OQ|·|OP|=|OR|,当点P在l上移动
时,求点Q的轨迹方程,并说明轨迹是什么曲线.
参考答案
一、选择题(本题考查基本知识和基本运算)
1.C 2.B 3.C 4.B 5.D 6.D 7.B 8.C 9 . A
10.D 11.B 12.C 13.A 14.D 15.A
二、填空题(本题考查基本知识和基本运算)
16.{x|-20,q>0.
n 1
(i)当q=1时,S=na,从而
n 1
S·S -
n n+2
=na·(n+2)a-(n+1)2
1 1
=- <0
(ⅱ)当q≠1时, ,从而
S·S -
n n+2
= .
由(i)和(ii)得S·S - .根据对数函数的单调性,知
n n+2
lg(S·S )0,使结论成立.
(ii)当q≠1时,若条件①成立,因为
(S—c)( S —c)-( S —c)2
n n+2 n+1
=
=-aqn[a-c(1-q)],
1 1
且aqn≠0,故只能有a-c(1-q)=0,即
1 1
此时,因为c>0,a>0,所以00,使结论成
立.
综合(i)、(ii),同时满足条件①、②的常数c>0不存在,即不存在常数c>0,使
.
证法二:用反证法,假设存在常数c>0,使
,
则有
①
②
③
由④得
④
SS - =c (S + S -2 S ). ⑤
n n+2 n n+2 n+1
第8页 | 共10页根据平均值不等式及①、②、③、④知
S + S -2 S
n n+2 n+1
=(S—c)+( S —c)-2(S —c) ≥2 -2( S —c)=0.
n n+2 n+1 n+1
因为c>0,故⑤式右端非负,而由(1)知,⑤式左端小于零,矛盾.故不存在常数
c>0,使
=lg( S —c)
n+1
26.本小题主要考查直线、椭圆的方程和
性质,曲线与方程的关系,轨迹的概念和求法,
利用方程判定曲线的性质等解析几何的基本思
想和综合运用知识的能力.
解法一:由题设知点Q不在原点.设P、
R、Q的坐标分别为(x,y),(x,y),(x,
P P R R
y),其中x,y不同时为零.
当点P不在y轴上时,由于点R在椭圆上及点O、Q、R共线,得方程组
解得
①
②
由于点P在直线l上及点O、Q、P共线,得方程组
解得 ③
④
当点P在y轴上时,经验证①-④式也成立.
由题设|OQ|·|OP|=|OR|2,得
第9页 | 共10页将①-④代入上式,化简整理得
因x与x同号或y与yp同号,以及③、④知2x+3y>0,故点Q的轨迹方程为
p
(其中x,y不同时为零).
所以点Q的轨迹是以(1,1)为中心,长、短半轴分别为 和 且长轴与x轴平行
的椭圆、去掉坐标原点.
解法二:由题设知点Q不在原点.设P,R,Q的坐标分别为(x,y),(x,y),(x,
p p R R
y),其中x,y不同时为零.
设OP与x轴正方向的夹角为α,则有
x=|OP|cosα,y=|OP|sinα;
p p
x=|OR|cosα,y=|OR|sinα;
R R
x=|OQ|cosα,y=|OQ|sinα;
由上式及题设|OQ|·|OP|=|OR|2,得
①
②
由点P在直线l上,点R在椭圆上,得方程组
, ⑤ ③
, ⑥ ④
将①,②,③,④代入⑤,⑥,整理得点Q的轨迹方程为
(其中x,y不同时为零).
所以点Q的轨迹是以(1,1)为中心,长、短半轴分别为 和 且长轴与x轴平行
的椭圆、去掉坐标原点.
第10页 | 共10页