文档内容
第一章 集合与常用逻辑用语章末检测
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.设集合 ,集合 ,则下列关系中正确的是( )
A. B.
C. D.
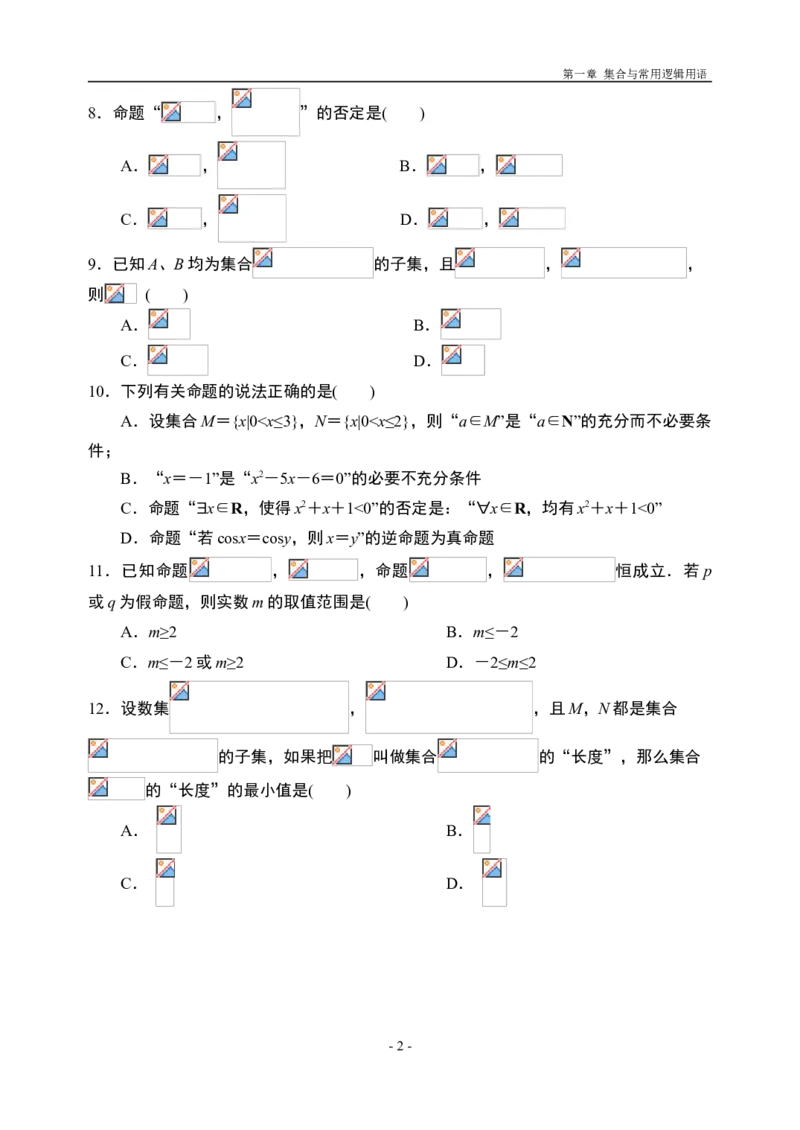
2.集合 , , ,
全集为 ,则图中阴影部分表示的集合是( )
A. B.
C. D.
3.已知集合 ,则满足 的集合 的个数是( )
A.2 B.3
C.4 D.8
4.集合 , ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知集合 满足 ,那么这样的集合 的个数为( )
A.5 B.6
C.7 D.8
6.设 ,则“ ”是“ ”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
7.若集合 中只有一个元素,则实数 的值为( )
A.1 B.0
C.0或1 D.以上答案都不对第一章 集合与常用逻辑用语
8.命题“ , ”的否定是( )
A. , B. ,
C. , D. ,
9.已知A、B均为集合 的子集,且 , ,
则 ( )
A. B.
C. D.
10.下列有关命题的说法正确的是( )
A.设集合M={x|02a+1}(a>0),若p是q
成立的充分不必要条件,求a的取值范围.
22.(本小题12分)已知集合A={x∈R|ax2-3x+2=0,a∈R}.
(1)若A是空集,求a的取值范围;
(2)若A中只有一个元素,求a的值,并把这个元素写出来;
(3)若A中至多有一个元素,求a的取值范围.
- 4 -第一章 集合与常用逻辑用语章末检测参考答案
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.设集合 ,集合 ,则下列关系中正确的是( )
A. B.
C. D.
【解析】A
∵M={x|x<4},N={x|04,而a>5 a>4,反之,不成立,
所以“A B”是“a>5”的必要不充分条件.
⇒ ⊆ ⇔ ⇒
5.已知集⊆合 满足 ,那么这样的集合 的个数为( )
A.5 B.6
C.7 D.8
【解析】C
根据题意,M集合一定含有元素1,2,且为集合{1,2,3,4,5}的真子集,所以集合M的个数
为23-1=7个,故选C.
6.设 ,则“ ”是“ ”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
【解析】C
由x>y推不出x>|y|,由x>|y|能推出x>y,所以“x>y”是“x>|y|”的必要不充分条件.
7.若集合 中只有一个元素,则实数 的值为( )
A.1 B.0
C.0或1 D.以上答案都不对
【解析】C
当k=0时,A={-1};当k≠0时,Δ=16-16k=0,k=1.故k=0或k=1.选C.
8.命题“ , ”的否定是( )
A. , B. ,
C. , D. ,
【解析】B
∵>0,∴x<0或x>1,∴命题“∀x>0,>0”的否定是 “∃x>0,0≤x≤1”
- 6 -9.已知A、B均为集合 的子集,且 , ,
则 ( )
A. B.
C. D.
【解析】D
由题意知,A中有3和9,若A中有7或5,则
∁U
B中无7和5,即B中有7或5,则与
A∩B={3}矛盾,故选D.
10.下列有关命题的说法正确的是( )
A.设集合M={x|0-1;再由q:
∀x∈R,x2+mx+1>0恒成立为假命题知m≥2或m≤-2,∴m≥2
12.设数集 , ,且M,N都是集合
的子集,如果把 叫做集合 的“长度”,那么集合
的“长度”的最小值是( )
A. B.
C. D.第一章 集合与常用逻辑用语
【解析】A
此题虽新定义了“长度”概念,但题意不难理解,只要求出M∩N,然后再求一个式子
的最小值即可;如何求M∩N呢?若真这样理解的话,就走弯路了.
其实,根本用不着求M∩N;集合M的“长度”是,由于m是一个变量,因此,这个长
度为的区间可以在区间[0,1]上随意移动;同理,集合N的长度为且也可以在区间[0,1]上
随意移动;两区间的移动又互不影响,因此M∩N的“长度”的最小值即为-=
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知集合A={(0,1),(1,1),(-1,2)},B={(x,y)|x+y-1=0,x,y∈Z},则A∩B
=________.
【解析】{(0,1),(-1,2)}
A、B都表示点集,A∩B即是由集合A中落在直线x+y-1=0上的所有点组成的集合,
将A中点的坐标代入直线方程检验知,A∩B={(0,1),(-1,2)}.
14.若命题“ ,使得 ”是真命题,则实数 的取值范围是
______.
【解析】由题意可知,Δ=(1-a)2-4>0,解得 或 .
15.设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=________.
【解析】1
∵3∈B,又a2+4≥4,∴a+2=3,∴a=1.
16.已知方程x2+(2k-1)x+k2=0,则方程有两个大于1的实数根(含相等两根)的充
要条件是 . .
【解析】 令f(x)=x2+(2k-1)x+k2,则方程x2+(2k-1)x+k2=0有两个大于1的实数
根
k<-2.
因此k<-2是使方程x2+(2k-1)x+k2=0有两个大于1的实数根的充要条件.
⇔⇔
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
- 8 -17.(本小题10分)已知全集 , ,
,求 的值.
【解析】2
由补集概念及集合中元素互异性知 应满足
分两种情况进行讨论:
在A中,由(1)得a=0依次代入(2)、(3)、(4)检验,不合②,故舍去。
在B中,由(1)得a=-3,a=2,分别代入(2、(3)、(4)检验,a=-3不合②,故舍
去,a=2能满足②③④,故a=2符合题意。
18.(本小题12分)已知集合 , .若
,则由实数 组成的集合 .
【解析】
当 时,集合 为空集,符合 .
当 时,A= , ,由 ,得 或 ,
即 或 ;第一章 集合与常用逻辑用语
所以 .
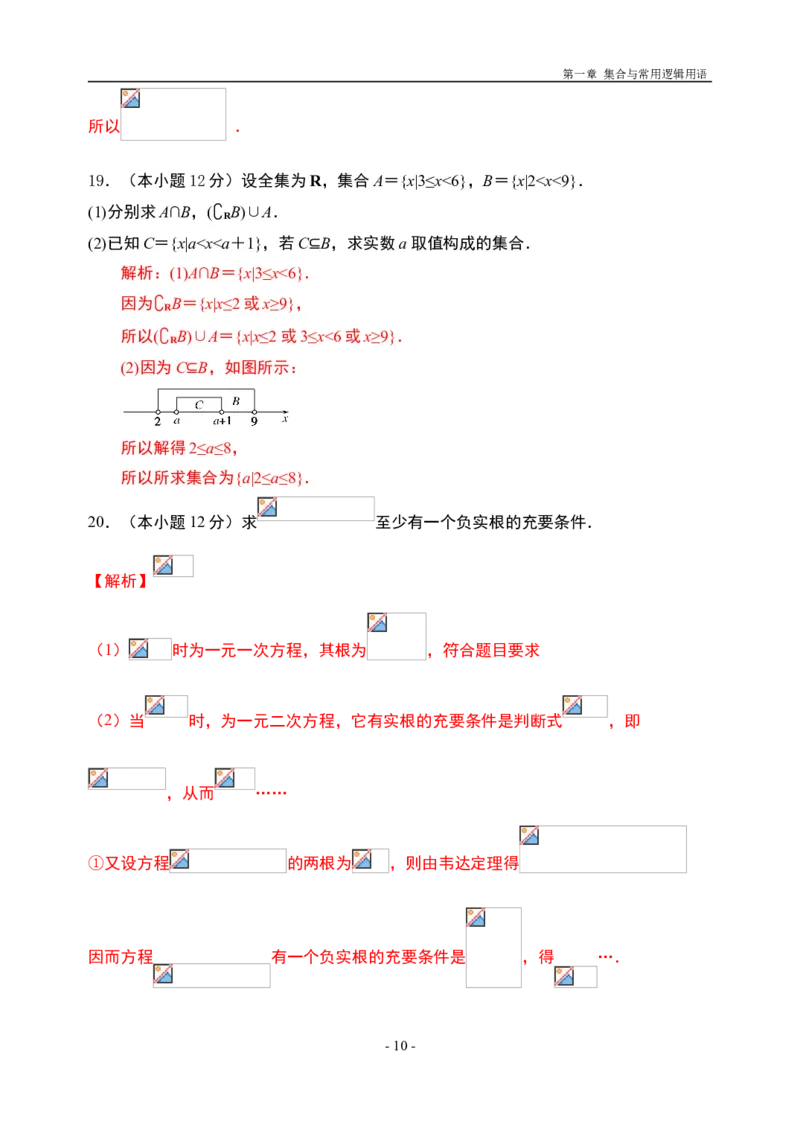
19.(本小题12分)设全集为R,集合A={x|3≤x<6},B={x|22a+1}(a>0),若p是q
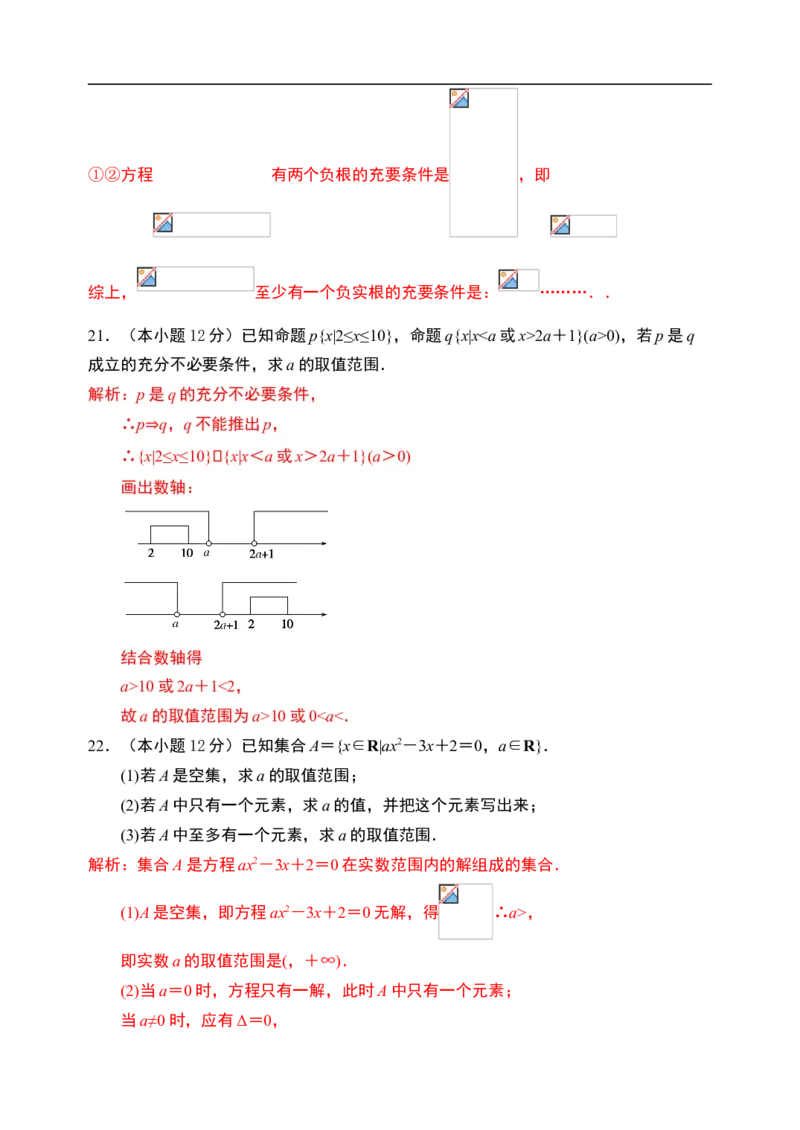
成立的充分不必要条件,求a的取值范围.
解析:p是q的充分不必要条件,
∴p q,q不能推出p,
∴{x
⇒
|2≤x≤10}{x|x<a或x>2a+1}(a>0)
画出数轴:
结合数轴得
a>10或2a+1<2,
故a的取值范围为a>10或0,
即实数a的取值范围是(,+∞).
(2)当a=0时,方程只有一解,此时A中只有一个元素;
当a≠0时,应有Δ=0,第一章 集合与常用逻辑用语
∴a=,此时方程有两个相等的实数根,A中只有一个元素,
∴当a=0或a=时,A中只有一个元素,分别是和.
(3)A中至多有一个元素,包括A是空集和A中只有一个元素两种情况,根据(1),(2)
的结果,得a=0或a≥,即a的取值范围是{a|a=0或a≥}.
- 12 -